Цена опциона. 
Формула Блэка — Шоулза

Дадим основные определения.

Опцион¹ как экономическое явление — это оформленное договором право купить, продать (или отказаться от сделки) на протяжении договорного срока и по фиксированной договорной цене определенный объем валюты, любых товаров, ценных бумаг (включая производные бумаги) либо получить определенный доход от финансового вложения или денежного займа (в виде разностной величины, фиксированного размера, процента).

Покупатель опциона — сторона договора, приобретающая право на покупку, продажу либо на отказ от сделки. Другими словами, это держатель опциона.

Продавец опциона — сторона договора, обязанная поставить или принять предмет сделки по требованию покупателя. Другими словами, это лицо, подписавшее опцион.

Опцион на покупку («колл», call) — это право, но отнюдь не обязанность, держателя опциона получить от лица, подписавшего опцион, определенную имущественную ценность (акцию, заем, фьючерсный контракт и т. д.) в заданный будущий момент времени (или в любой момент определенного промежутка времени) по заранее установленной цене.

Опцион на продажу («пут», put) — данное право, но отнюдь не обязанность, продать имущественную ценность в определенный будущий момент (или промежуток) времени по заранее оговоренной цене.

Различают европейский опцион, при котором это право (на покупку или на продажу) может быть реализовано только в момент наступления срока истечения опционного контракта, и американский опцион, при котором это право (соответственно, покупки или продажи) может быть реализовано в любое время в пределах опционного срока.

' Die Option (нем.) — первоначально юридический термин, означающий оптацию, т. е. выбор подданства или гражданства.

Обозначим:

S — спот-цена базисного актива, т. е. сегодняшний биржевой курс того продукта, на покупку или продажу которого заключается опционный контракт;

К — страйк, т. е. та цена купли-продажи, которая оговорена в опционе;

Т — оставшийся срок (в годах) до даты истечения контракта;

а — волатильность биржевого курса базисного актива, т. е. среднее квадратическое отклонение изменения в единицу времени цепы того блага, на которое заключается опционный контракт;

r_F — безрисковая ставка процента (годовая).

Теоретическая (равновесная) цена европейского ^//-опциона согласно формуле Блэка — Шоулза равна.

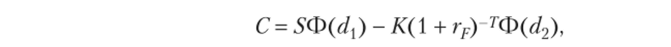
где 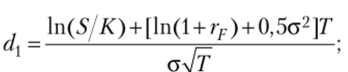Ф — функция распределения стандартного нормального закона; d₂ = d_{ -aVr.

Теоретическая (равновесная) цена европейского put-опциона согласно формуле Блэка — Шоулза равна.

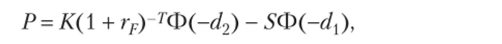
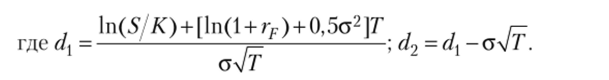
Часто вместо безрисковой годовой процентной ставки r_F в формулах Блэка — Шоулза используется более удобная для теоретического рассмотрения номинальная годовая безрисковая процентная ставка при условии непрерывного начисления процентов, другими словами — сила роста непрерывно начисляемых процентов R_F, связанная с r_F соотношением 1 + r_F = e^Rr, или R_f= ln (l + Гр). Тогда все формулы Блэка — Шоулза очевидным образом модифицируются заменой ln (l + r_F) на R_F и (1 + Гр)~^т на exp (-R_FT).

Цена, по которой можно купить опцион, называется его премией.

Рассмотрим вывод дифференциального уравнения Блэка — Шоулза. Предположим, что цена актива S подчинена закону геометрического броуновского движения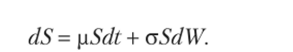

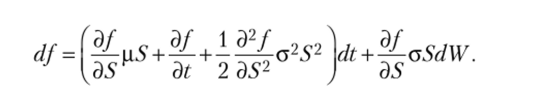
Предположим, что / — цена производного финансового инструмента на S. Тогда /должна быть некой функцией от S и /. Следовательно, по формуле Ито Построим динамический портфель, состоящий из короткой позиции.

«Э/.

по одной единице производного инструмента / и длинной позиции по -г-

oS

" Л г

единицам актива S. Тогда ценность портфеля П равна П = -/S, а ее.

aS

изменение за короткий промежуток времени dt есть.

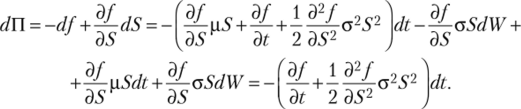
Так как полученное выражение не содержит члена с dW, портфель П остается безрисковым в течение короткого промежутка времени dt и должен поэтому из условия отсутствия арбитража приносить за время Атакую же доходность на вложенный капитал, как и любой другой краткосрочный безрисковый финансовый актив, т. е.

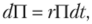
где г — безрисковая процентная ставка. Таким образом, получаем.

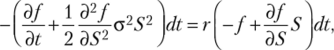
или.

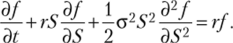
Получено дифференциальное уравнение Блэка — Шоулза. Оно имеет множество решений, соответствующих всем различным производным финансовым инструментам, которые можно определить на основе актива S. Получаемые частные решения зависят от различных граничных условий, соответствующих тому или иному производному инструменту. Для европейского «///-опциона основное граничное условие имеет вид / = шах (Д — X, 0), если t = Т, где К — страйк, а Т — срок исполнения опциона. В случае же европейского рШ-опциона оно принимает вид / = max (X — S, 0), если I = Т.