Плоская симметрия. 
Физика. 
Механика. 
Электромагнетизм

Пусть распределение заряда таково, что р (х, у, z) = р (х), т. е. в плоскости х = const (в плоскости, параллельной yOz) плотность заряда постоянна. Симметрия такова, что при сдвигах всего пространства, определяемых вектором а = yi + zk, при любых у, z ничего не меняется. Поле будет обладать такой же симметрией, т. е. при указанных сдвигах переходить в себя. Это оставляет для вектора D одну возможность:

Как и ранее, симметрия снижает число неизвестных функций с трех (три компоненты вектора D) до одной, что позволяет решить проблему на базе одного интегрального уравнения для D:

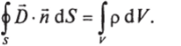
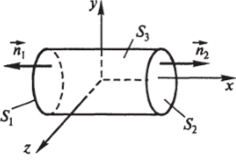
Рис. 7.34.

В качестве S возьмем цилиндрическую поверхность 5₃ с образующей вдоль оси х, замкнутую двумя ортогональными сечениями 5, и S₂ (рис. 7.34). Имеем:

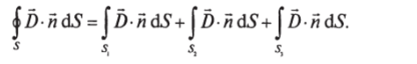
Интеграл по S₃ равен нулю (почему?), а для двух других получим.

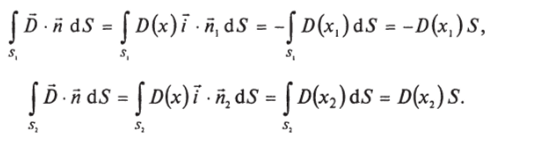
Здесь учтено, что й, = - /, й₂ = /' Дх,) — индукция в сечении х, Дх₂) — в сечении х₂, S — площадь сечения. Таким образом,.

Интеграл в правой части (7.40) представляет заряд, оказавшийся внутри замкнутой поверхности. Так как р = р (х), интегрирование удобно вести по слоям толщиной dx. Имеем: d К = 5dx, так что из (7.40) получаем.

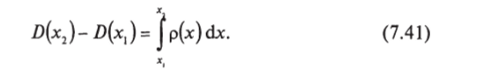
Величина j p (x)dx есть заряд, заключенный между сечениями 5, и.

Xj.

5₂, приходящийся на единицу площади сечения.

В уравнении (7.41) две неизвестные величины Дх₂) и Дх,), поэтому одного уравнения мало. В качестве дополнительного условия наложим следующее: вне заряженного слоя поле D однородно, векторы D по разные стороны слоя равны по величине и противоположно направлены. Если распределение заряда р (х) обладает плоскостью симметрии, это условие очевидно; если симметрии нет, оно тем не менее верно.

Задача 7.12. Имеем равномерно заряженный слой толщиной dс плотностью заряда р (х) = р = const. На расстоянии / от слоя находится слой диэлектрика толщиной d_{ (рис. 7.35). Ищем поле во всем пространстве.

Решение. Математическое описание ситуации таково:

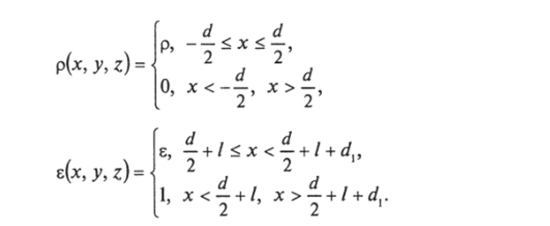
Поле D вне слоя находится немедленно. Имеем:

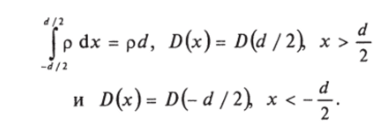
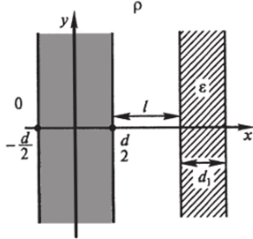
Рис. 7.35.

Уравнение (7.41) для двух сечений х₂ = d/2 и х, = — d/2 дает.

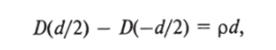
так что D (d / 2) = -D (- d / 2) = рd/2 и окончательно имеем.

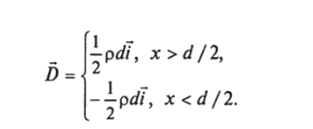
Что касается поля внутри слоя, то для х из области х еу, у уравнение (7.41) дает.

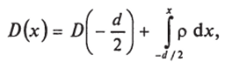
откуда D (x)= D (- d/2)+ р (х +d/2) = - pd/2 + рх + prf/2 = рх. Таким образом, в области хе -у, у ^поле D меняется линейно.

1, 1 ,.

от —рд доре.

2 2.

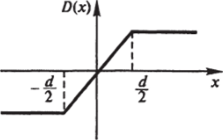
Итак, для поля D во всем пространстве получаем (рис. 7.36):

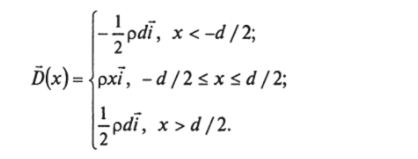
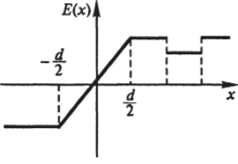
Для напряженности поля Е по формуле ?(х) = ?>(х)/ее₀ находим (рис. 7.37):

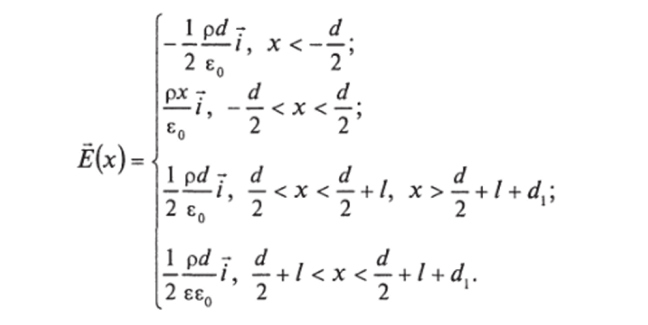
Задача 7.13. Имеем две заряженные параллельные пластины. Заряды пластин — q_{ и q₂. Найти поле во всем пространстве.

Решение. Надо понимать, что это вовсе не простая задача. Пусть / — характерный линейный размер пластин. На больших расстояниях (при г «I) поле будет мало отличаться от поля точечного заряда: Е «q/4ne₀r², где q = q_x + q₂ — полный заряд. На малых расстояниях поле зависит от формы пластин, расстояния между ними, распределения заряда на пластинах, и вычисление поля — трудная задача. Но если расстояние между пластинами d достаточно мало (d 2 постоянна, поле вблизи пластин можно найти по приведенным выше формулам для бесконечных пластин. В этом приближении будем иметь следующее.

Пусть первая плоскость будет х = 0, вторая — х = d. Выберем два сечения х = х₁<0их = х₂>^ (рис. 7.38). Для этих сечений по формуле (7.41) получим D (х₂) — D (x_t) = о = о, + а_г

Поскольку D (x₂) = — /)(*,), находим, что D (x₂) = (а, + а₂)/2,.

D (xj) = —(Oj + а₂)/2. Таким образом, при x>d D = (о, + а₂)/2/,.

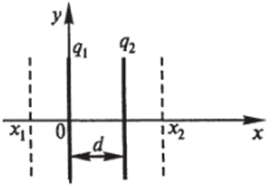
Рис. 7.38.

при х < О D = - (б, + 5₂)/2 /. Чтобы найти поле между плоскостями (при 0 < х < d), применим формулу (7.41) для сечений х и x_t: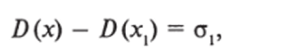

откуда D (x) = Z)(Xj) + о, = -(о, + а₂)/2 +.

+ Oj = (о, — о₂)/2.

Для разности потенциалов будем иметь:

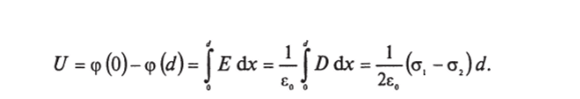
Рассмотрим некоторые частные случаи. На рис. 7.39—7.42 изображены поля Е и графики зависимости Е от х.

1) о, > о₂ > О.

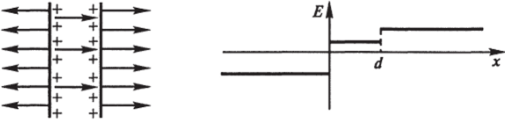
Рис. 7.39.

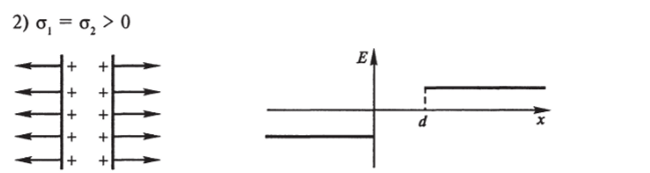
Рис. 7.40.

Рис. 7.41.

4) Плоский конденсатор, q_t + q₂ — 0, q_{ = aS, q₂ = —aS.

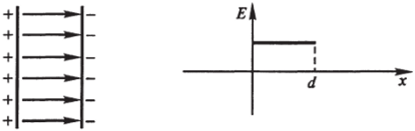
В этом случае.

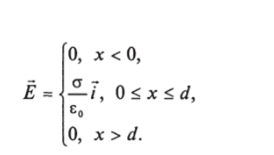
Разность потенциалов между пластинами U = Ed = —.

^Ео Обратите внимание на примеры 2) и 3). Разность потенциалов между пластинами в этих случаях U = Ed = 0. Это означает, что их можно соединить проводником, и ничего не изменится. А это, в свою очередь, означает, что эти случаи соответствуют полю, создаваемому заряженным проводником в виде слоя толщиной d.

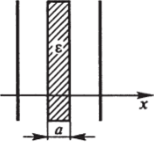
Рис. 7.43.

Е = о/ее₀ внутри Задача 7.14. Между двумя проводящими пластинами поддерживается разность потенциалов U. Расстояние между пластинами d. Между пластинами находится слой диэлектрика толщиной а с проницаемостью е (рис. 7.43). Найти заряд на пластинах.

Решение. Если d много меньше наименьшего линейного размера пластины, приближенно годятся формулы для плоской симметрии. Ситуация соответствует случаю 4) предыдущей задачи.

Имеем: D = а, Е — о/е₀ вне диэлектрика и диэлектрика. Разность потенциалов откуда.

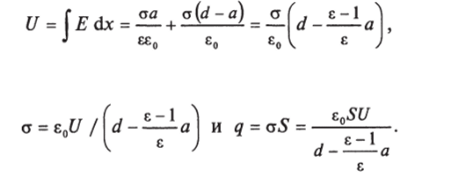
Устройство такого рода называется плоским конденсатором, а коэффициент пропорциональности между зарядом и напряжением называется емкостью. Таким образом, емкость нашего конденсатора равна С = с₀S /{d — -—- я j. Если диэлектрик отсутствует, следует положить либо а — 0, либо е =1.

Выводы;

При хорошей симметрии источника поле определяется одной скалярной функцией, для нахождения которой достаточно одного уравнения.

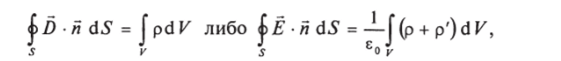
где р' — плотность связанных зарядов.

При сферической симметрии индукция поля D на сфере радиусом г равна где q® — заряд, оказавшийся внутри сферы.

При цилиндрической симметрии индукция D на поверхности цилиндра радиусом R

где 6(Л) — заряд внутри цилиндра, приходящийся на единицу длины цилиндра.

При плоской симметрии.

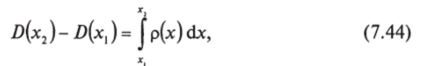
где Щх) — значение индукции D на плоскости х — const.