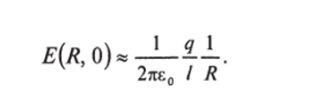Уравнение для потенциала

Из уравнения (7.46) следует.

(мы уже обсуждали этот факт), поэтому уравнение (7.45) можно записать в виде.

?* - ^ ^.

Оператор V • V = V² = —- + —- + —- есть скалярный оператор (в.

дх ду дг

отличие от V) и называется оператором Лапласа (иногда обозначается символом Д). Если е не зависит от координат, уравнение (7.51) принимает вид

Именно это уравнение (оно называется уравнением Пуассона) является ключевым в электростатике. Крупный раздел математики посвящен решению этого уравнения.

Если задано распределение зарядов и расположение и форма проводников и диэлектриков, это уравнение в принципе может быть решено, т. е. может быть найдена функция ф (г) — потенциал электрического поля. (В общем случае — это сложная математическая проблема, которую мы и обсуждать не будем.) Если потенциал Ф известен, напряженность Е находится простым дифференцированием по формуле (7.50).

Поле, создаваемое заданным распределением заряда. Поле диполя

Трудности, связанные с нахождением поля, возникают из-за того, что распределение зарядов в проводниках и диэлектриках само подлежит определению и может быть найдено лишь совместно с полем. Если же распределение заряда известно, решение уравнения (7.52) можно легко сконструировать. В основе решения лежит принцип суперпозиции: напряженность поля в данной точке, создаваемого совокупностью зарядов, равна сумме напряженностей от каждого заряда в отдельности. Это верно и для потенциала.

Пусть распределение плотности заряда р (г) задано. Нас интересует поле в точке Р, определяемой радиусом-вектором R-[X, Y, Z) (рис. 7.44). Разбиваем всю область распределения заряда на элементарные объемы. Пусть dV — такой объем. Его положение задается радиусом-вектором г = (х, у, z) — В этом элементе содержится заряд d q = pdK Этот заряд можно рассматривать как точечный, и поле такого заряда известно. В частности, в точке Р напряженность.

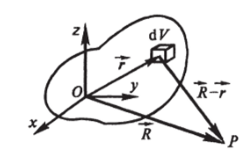
Рис. 7.44.

dЕ_р и потенциал dф_/>, создаваемые этим зарядом, будут:

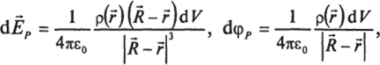
где (л~г) — вектор, идущий из dV в Р, |Л-г| — его длина.

Напряженность и потенциал поля в точке Р получим, суммируя поля всех элементарных зарядов:

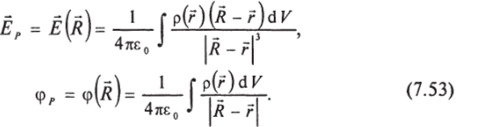
Интегрирование ведется по переменной V по всему пространству, т. е. фактически по области, в которой р * 0. Эти формулы решают проблему. Могут быть, конечно, технические трудности в вычислении интеграла, но идейных проблем нет.

Как правило, по формуле (7.53) ищут потенциал, а напряженность находят по потенциалу: Е = -VЕ, помня о том, что Ё — вектор и интеграл представляет векторную сумму.

Задача 7.16. Пусть поле создается участком равномерно заряженной плоскости с поверхностной плотностью заряда, а = const Найти напряженность электрического поля в произвольной точке Р.

Решение. Для напряженности поля в точке Р (рис. 7.45) формула (7.53) дает.

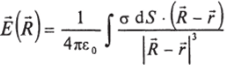
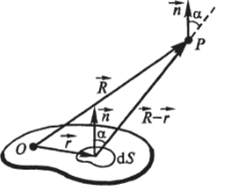
Рис. 7.45.

(вместо pdKпишем od5). Умножим обе части равенства на единичный вектор нормали к плоскости Я. Постоянный вектор Я может быть внесен под знак интеграла. Будем иметь:

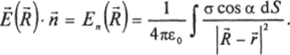
Величина —— — есть телесный угол бй, под которым элемент d5.

М виден из точки Р, а интеграл jdft = й есть полный телесный угол, под которым наш участок плоскости виден из точки Р. (Телесный угол из центра сферы радиусом г вырезает из поверхности сферы кусок площадью йг². Величина телесного угла по определению есть й = S/r)

Окончательно получаем.

т. е. нормальная составляющая напряженности, создаваемой участком заряженной плоскости, определяется телесным углом, под которым виден этот кусок из точки, в которой определяем поле.

Этот результат не только красив, но и полезен. Например, бесконечная плоскость из любой точки видна под углом 2л, поэтому напряженность? в любой точке будет о/2е₀. Из соображений симметрии следует, что? есть полная напряженность. Этот результат нам уже знаком.

Решение. Имеем:

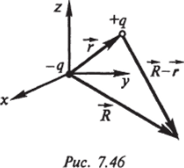
Задача 7.17. Рассмотрим поле диполя.

Имеем два одинаковых точечных заряда с противоположными знаками. Пусть заряд — q находится в начале координат, а заряд q — в точке г (рис. 7.46). Найти напряженность и потенциал в произвольной точке, расположенной на расстоянии R от начала координат.

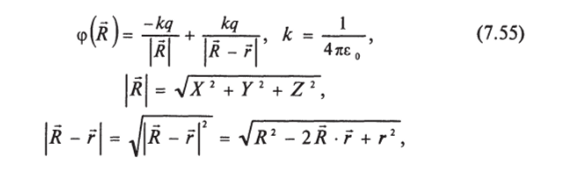
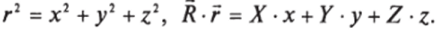
Напряженность поля в точке R находится простым дифференцированием: Е_х = — Эср/ЭЛ' и т. д.

Для больших расстояний R «г формулу (7.55) можно упростить. Тогда для R-r, опуская г², получим.

(здесь мы воспользовались тем, что (1+х)^я «1 + пх при д: «1). Формула (7.55) принимает вид.

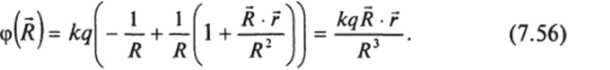
Величина qr для такой системы зарядов называется дипольным моментом, а сама система — диполем. Обозначая дипольный момент р, перепишем формулу (7.56):

Эта формула дает потенциал поля, создаваемого точечным диполем, находящимся в начале координат. Для напряженности поля получим.

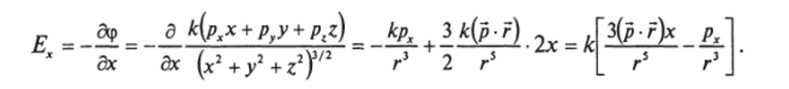
Для Е_у и E_z результат можно написать сразу, заменяя символ х на у и на Z- В векторной форме.

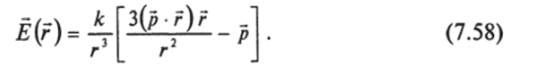
Пусть р = pi (диполь ориентирован вдоль оси х (рис. 7.47)). Для точки (х, 0, 0) имеем:

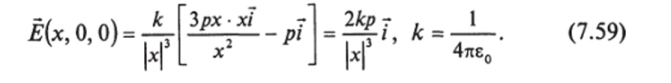
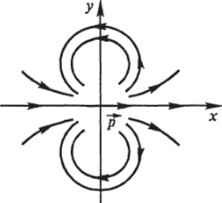
В точке (0, у, 0).

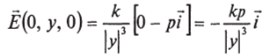
_{Рис 7}47 Рассмотрим дипольный момент. Для.

(для этой точки р? = 0). Поле диполя изображено на рис. 7.47. Вблизи начала координат поле не обозначено, так как решение в любом случае верно на некотором расстоянии от начала.

Рассмотрим дипольный момент. Для произвольного распределения заряда ве;

произвольного распределения заряда величина р = — сумма по всем заряженным частицам, где —.

радиус-вектор частицы с зарядом q_/y — называется дипольным моментом распределения. В интегральной форме p = jp®r dK. Если.

V

полный заряд равен нулю, т. е. ег/₍ = 0, распределение можно разбить на элементарные диполи типа рассмотренного выше, и тогда полный дипольный момент есть сумма этих элементарных диполей:

р = } р_г На больших расстояниях от этого распределения поле будет определяться формулами (7.57), (7.58). Например, многие молекулы, будучи нейтральными, обладают отличными от нуля дипольными моментами.

Другим примером может быть проблема, с которой мы столкнулись при обсуждении поля плоского конденсатора (см. п. 7.1.2).

Плоский конденсатор обладает дипольным моментом р = qd, и на больших расстояниях от конденсатора его поле определяется формулами (7.57), (7.58).

7.4.4. Поле, создаваемое тонким стержнем.

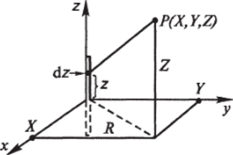
Рис. 7.48 244.

Пусть заряд q равномерно распределен по тонкому стержню длиной /. Стержень расположен вдоль оси z, начало координат — в середине стержня (рис. 7.48). Очевидно, поле обладает осевой симметрией (ось совпадает со стержнем) и плоскостью симметрии (плоскость, ортогональная стержню и проходящая через его середину).

Вместо pd Vпишем (q/l)dz — это заряд элемента стержня длиной dz- Полагая X² + Y² = R² и делая замену Z — z — и, приводим интеграл к табличному. В результате получаем.

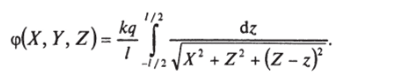
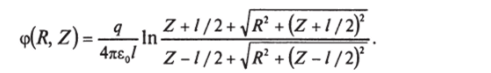
Это решение справедливо при z > 0. Поскольку плоскость z = 0 — плоскость симметрии, решение, справедливое всюду, имеет вид.

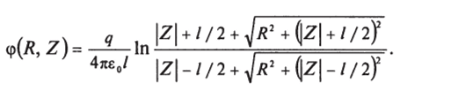
Отсюда для поля на оси z находим.

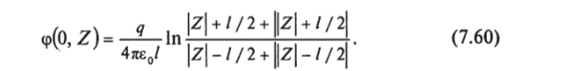
Потенциал в плоскости симметрии z = 0.

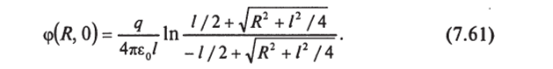
При малых R (с учетом (1+х)" = 1+"х) эта формула приводит к.

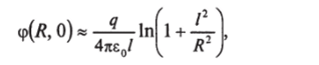
так что для напряженности поля в плоскости симметрии при малых R получим.

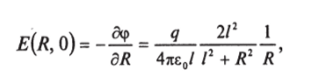
вектор Ё лежит в плоскости z — 0 и направлен вдоль луча из начала координат. При R /.

Полезно сопоставить эти результаты с тем, что мы имели для поля бесконечного заряженного цилиндра.