Линейная парная регрессия

Данные о статистической зависимости удобно задавать в виде корреляционной таблицы.

Рассмотрим в качестве примера зависимость между суточной выработкой продукции Y (т) и величиной основных производственных фондов X (млн руб.) для совокупности 50 однотипных предприятий (табл. 12.1).

Таблица 12.1.

(В таблице через x_i и г/_; обозначены середины соответствующих интервалов, а через п_х и п_} — соответственно их частоты.).

Изобразим полученную зависимость графически точками координатной плоскости (рис. 12.2). Такое изображение статистической зависимости называется полем корреляции.

Для каждого значения x_t(i = 1, 2, …, /), т. е. для каждой строки корреляционной таблицы, вычислим групповые средние.

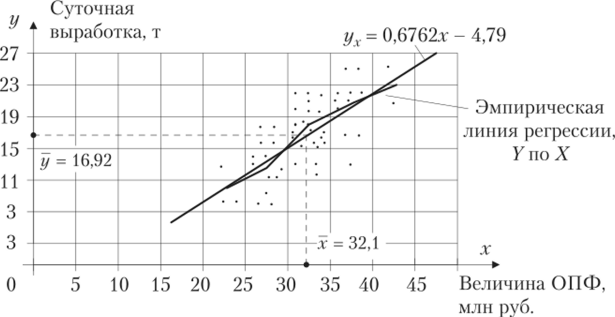
Рис. 12.2.

т

где rijj — частоты пар {х, у_}) и n-_t = Yj ⁿij> ^т ~ число интервалов по переменной Y. ¹⁼¹

Вычисленные групповые средние у_{ поместим в последнем столбце корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии V по X (см. рис. 12.2).

Аналогично для каждого значения у_} (j = 1,2,…, т) по формуле.

вычислим групповые средние Xj (см. нижнюю строку корреляционной /.

таблицы)^[1], где =? п_{/, / — число интервалов, но переменной X.

i=1.

По виду ломаной можно предположить наличие линейной корреляционной зависимости Y но X между двумя рассматриваемыми переменными, которая графически выражается тем точнее, чем больше объем выборки (число рассматриваемых предприятий) п:

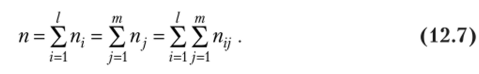
Поэтому уравнение регрессии (12.3) будем искать в виде.

Отвлечемся на время от рассматриваемого примера и найдем формулы расчета неизвестных параметров уравнения линейной регрессии.

С этой целью применим метод наименьших квадратов, согласно которому неизвестные параметры Ь₍₎ и Ь_] выбираются таким образом, чтобы сумма квадратов отклонений эмпирических групповых средних y_t, вычисленных по формуле (12.5), от значений у_х., найденных по уравнению регрессии (12.8), была минимальной:

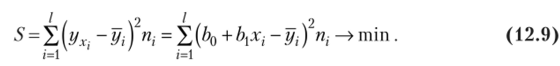
На основании необходимого условия экстремума функции двух переменных S = S (b₀, b_{) приравниваем к нулю ее частные производные, т. е.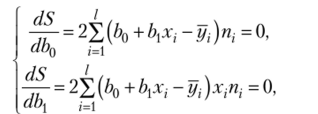

откуда после преобразовании получим систему нормальных уравнении для определения параметров линейной регрессии:

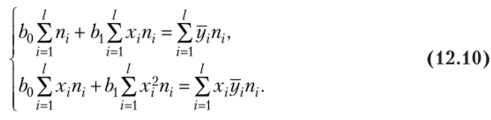
Учитывая (12.5), преобразуем выражения:

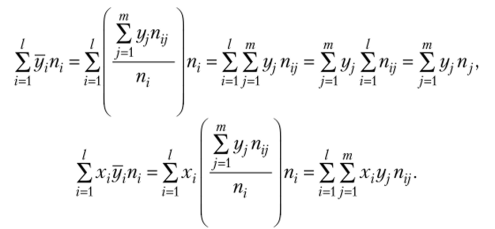
Теперь с учетом (12.7), разделив обе части уравнений (12.10) на п, получим систему нормальных уравнений в виде.

где соответствующие средние определяются по формулам.

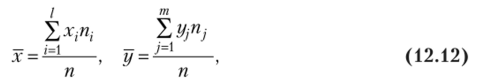
Подставляя значение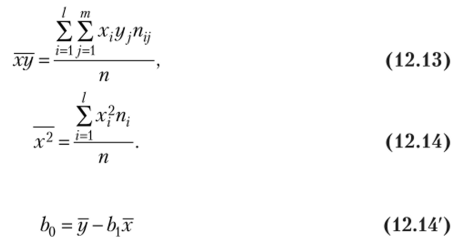

из первого уравнения системы (12.11) в уравнение регрессии (12.8), получим у_х=уЬ_{х + ЬХ, или.

Коэффициент Ь_{ в уравнении регрессии, называемый выборочным коэффициентом регрессии (или просто коэффициентом регрессии) Y по X, будем обозначать символом Ь_ух. Теперь уравнение регрессии Y по X запишется так:

Коэффициент регрессии Y по X показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу.

Решая систему (12.11), найдем.

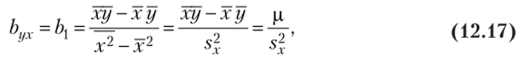
где s² — выборочная дисперсия переменной X (см. формулу (8.10)):

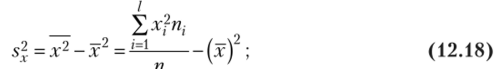
р — выборочный корреляционный момент или выборочная ковариация^[2]:

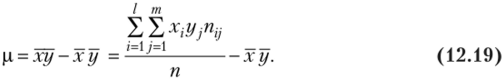
Рассуждая аналогично и полагая уравнение регрессии (12.4) линейным, можно привести его к виду

c6v (X, У), 4,.

где.

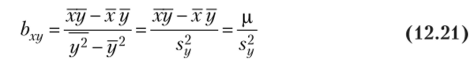
— выборочный коэффициент регрессии (или просто коэффициент регрессии) X по У, показывающий, па сколько единиц в среднем изменяется переменная X при увеличении переменной Y на одну единицу,

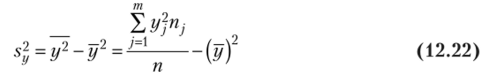
— выборочная дисперсия переменной У.

Так как числители в формулах (12.17) и (12.21) для Ь_ух и й совпадают, а знаменатели — положительные величины, то коэффициенты регрессии Ь_ух и Ь_ху имеют одинаковые знаки, определяемые знаком р. Из уравнений регрессии (12.16) и (12.20) следует, что коэффициенты Ь_ух и 1 /Ь_ху определяют угловые коэффициенты (тангенсы углов наклона) к оси Ох соответствующих линий регрессии, пересекающихся в точке (х, у) (см. рис. 12.4).

t> Пример 12.1. По данным табл. 12.1 найти уравнения регрессии У по X и X по У и пояснить их смысл.

Решение. Вычислим все необходимые суммы:

(обходим все заполненные клетки корреляционной таблицы).

Затем по формулам (12.12)—(12.22) находим выборочные характеристики и параметры уравнений регрессии:

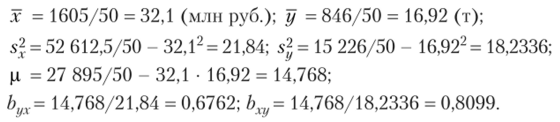
Итак, уравнения регрессии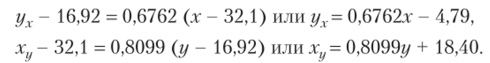

Из первого уравнения регрессии Y но X (его график показан на рис. 12.1) следует, что при увеличении основных производственных фондов (ОГ1Ф) X на 1 млн руб. суточная выработка продукции Y предприятия увеличивается в среднем на 0,6762 т. Второе уравнение регрессии X по Y показывает, что для увеличения суточной выработки продукции Y на 1 т необходимо в среднем увеличить ОПФ X на 0,8099 млн руб. (отметим, что свободные члены в уравнениях регрессии не имеют реального смысла). ?

Параметры уравнений регрессии (12.8) могут быть вычислены упрощенным способом^[3] (аналогично тому, как вычислялись числовые характеристики вариационного ряда в параграфе 8.4). С этой целью от значений.

х- — с У i ~с'

переменных х. и и-. переходят к новым значениям и. =—— и гл =——, где ¹ k^[3] к

к и к' — величины интервалов, а с и с' — середины серединных интервалов соответственно по переменной X или Y. Тогда в соответствии с формулами (8.20) и (8.21).

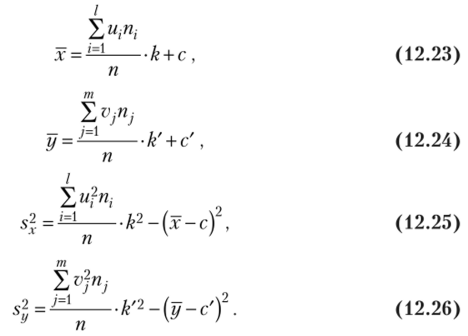
В этом случае формула для ковариации р (12.19) примет вид.

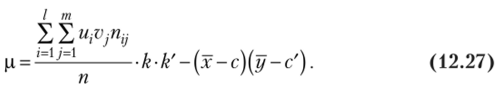
[> Пример 12.2. По данным табл. 12.1 найти упрощенным способом уравнения регрессии Y по X и X по Y и пояснить их смысл.

Решение. Возьмем постоянную к равной величине интервала по переменной X, т. е. к = 5, а постоянную с — равной середине серединного, третьего, интервала, т. е. с = 32,5. Аналогично по переменной F к'- 4, с' -17.

Итак, щ = (Xj- 32,5)/5; Vj = (у_} — 17)/4. Представим корреляционную табл.

12.1 в виде табл. 12.2.

Таблица 12.2.

Вычислим необходимые суммы:

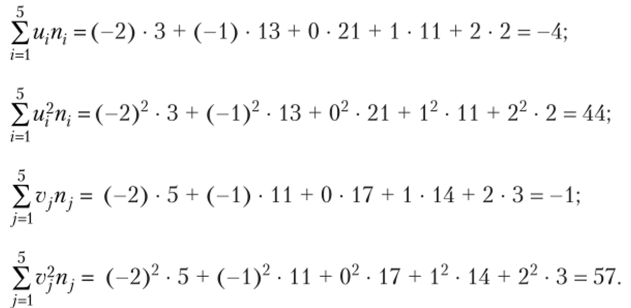
Для упрощения вычислений расчеты указанных сумм целесообразно проводить непосредственно в таблице (см. соответственно два предпоследних столбца и две предпоследние строки со значениями необходимых сумм в итоговых строке и столбце).

5 5.

Для удобства вычисления суммы? ? ^ui^vjⁿij вначале рассчитываем upj

i=ij=

и проставляем эти значения под соответствующими частотами, а затем находим произведения (upj)n^ которые суммируем по строке и столбцу, и записываем полученные числа соответственно в последнем столбце и последней строке табл. 12.2. Например, на пересечении первой строки и первого столбца табл. 12.2 получим 2₄, т. е. частота п_п = 2, u_{v_x = (-2)(-2) = 4, a (u_{v_x)n_n = 4 • 2 = 8 и т. д. Итак, суммируя произведения ир_}п^ в последнем столбце или в последней строке, получим в правом нижнем углу табл. 12.2.

tt и_т= 37.

*=1.7=1.

Теперь по формулам (12.23)—(12.27) имеем:

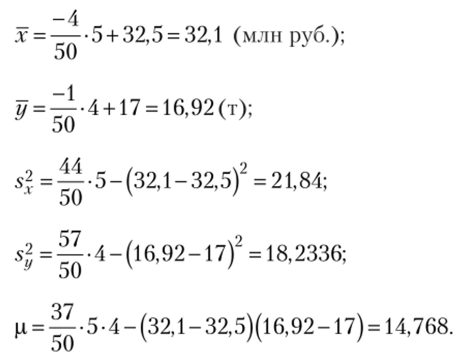
Далее уравнения регрессии находятся и интерпретируются так же, как в примере 12.1. ?

• [1] Чтобы не загромождать чертеж, эмпирическая линия регрессии X, но У на рис. 12.2не показана.
• [2] Для выборочной ковариации переменных X и Y используется также обозначение
• [3] См. сноску на с. 261.
• [4] См. сноску на с. 261.