Нахождение проекций точек на изображениях геометрических тел

Геометрические тела. Формообразующей основой всех машиностроительных деталей являются геометрические тела. Геометрическое тело — это часть пространства (компактное множество точек), ограниченная замкнутой поверхностью. Все геометрические тела делятся на тела вращения и многогранники.

Тела вращения — это объемные тела, образованные вращением плоской геометрической фигуры вокруг некоторой линии, называемой осью. В табл. 2.1 приведены примеры простейших тел вращения.

Поверхность, ограничивающая шар, называется сферической. Поверхность, ограничивающая цилиндр, называется цилиндрической. Поверхность, ограничивающая конус, называется конической.

Тела вращения.

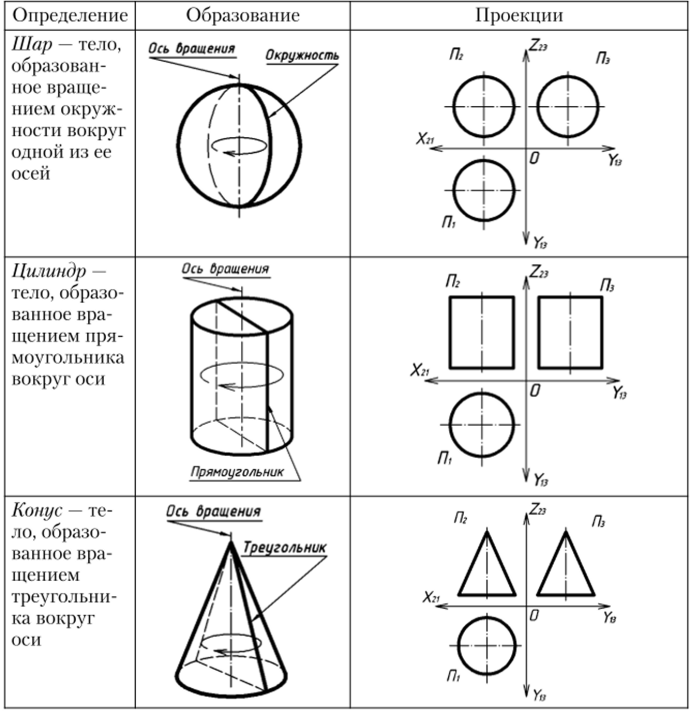
Плоскости, ограничивающие цилиндр и конус, называются основанием.

Многогранник — это геометрическое тело, ограниченное плоскостями. Элементами многогранника являются ребра, грани и основания. Если в основании многогранника лежит правильный многоугольник, а его ось перпендикулярна основанию, то многогранник называется правильным.

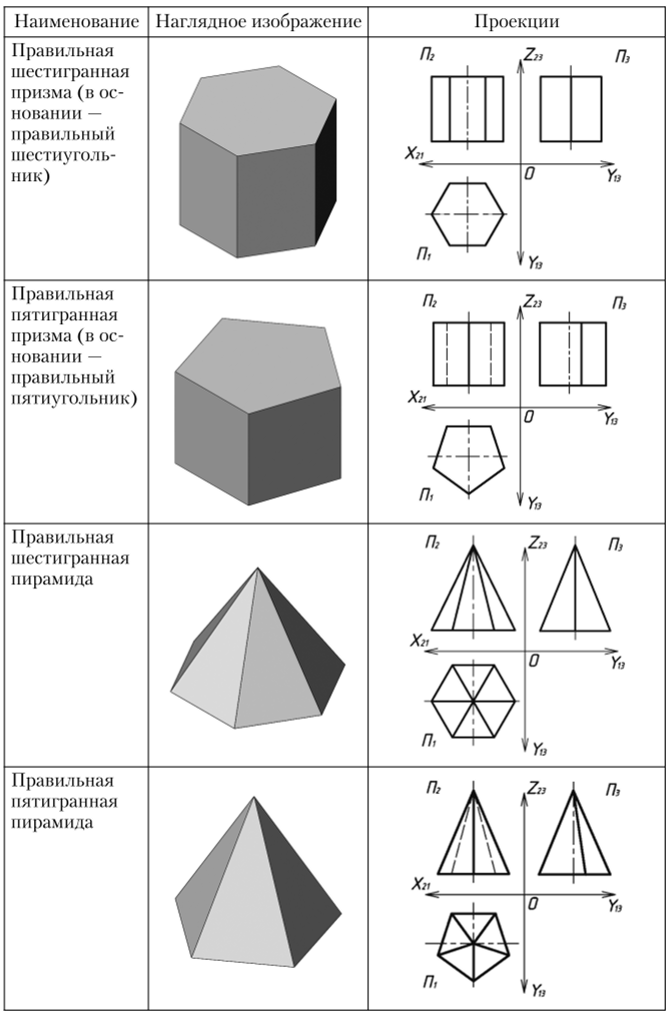
Многогранники делятся на призмы и пирамиды. В табл. 2.2 приведены примеры наиболее распространенных многогранников.

Для развития пространственного мышления весьма полезными являются задания, связанные с нахождением проекций точек, принадлежащих поверхностям геометрических тел.

Многогранники.

Построение проекций точки. Точка А принадлежит поверхности Т, если она принадлежит линии а, лежащей на этой поверхности:

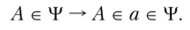
Очевидно, что такой линией может быть любая линия поверхности, но целесообразным является выбор наиболее простых в построении линий — прямых или окружностей.

На рис. 2.5, а представлено построение проекций точки на трех плоскостях: П₂ — фронтальной, П, — горизонтальной, П₃ — профильной. Линии X, У, Z представляют собой систему координат с началом в точке О. Точки Л, Л₂, Л₃ — проекции точки Л на плоскостях; отрезки А_х, А, А_г — координаты х, у, 2 точки Л, отложенные на соответствующих осях.

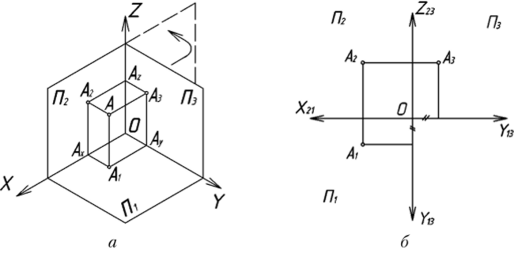
Рис. 2.5. Построение проекций точки.

Преобразуем три плоскости проекций в одну, приняв в качестве плоскости чертежа плоскость II ,. При этом плоскость П, поворачивается вокруг оси X, плоскость Я₃ — вокруг оси Z (рис. 2.5, б) (заметим, что теперь ось Yприсутствует дважды). Из рис. 2.5 следует, что каждая из проекций точек определяется двумя координатами: Л,(х, г/), Л₂(х, г), Л₃(г, у).

Обращаем внимание читателя на наличие проекционной связи между проекциями точек: вертикальная линия между А., и Л, горизонтальная — между Л₂ и Л₃.

Система координат X, У, Z является внешней по отношению к проецируемому объекту (на рис. 2.5 проецируемый объект — точка). При выполнении изображения геометрического тела (предмета) целесообразно установить в нем внутреннюю систему координат, приняв в качестве оси Z вертикальную ось тела (предмета). При этом оси X, Y будут ей перпендикулярны (рис. 2.6).

Тогда при изображении проекции тела на плоскостях П, П₂, П₃ будут присутствовать оси внутренней системы координат, относи;

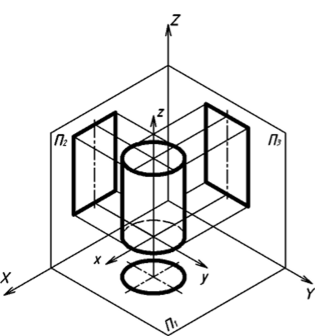
Рис. 2.6. Внутренняя система координат.

тельно которой можно строить проекции точек, принадлежащих поверхности тела.

Формулировка задачи: по заданной проекции точки на изображении тела постройте ее недостающие проекции.

Алгоритм построения проекций точек на поверхностях тел

заключается в следующем:

• 1) через заданную проекцию точки проводим линию, принадлежащую поверхности тела;
• 2) строим проекции этой линии на других изображениях тела;
• 3) на проекциях линии находим соответствующие проекции точек.

Рассмотрим примеры нахождения недостающих проекций точек на изображениях основных геометрических тел. Примем следующие обозначения проекций точек:

± заданная проекция точки;

+ видимая проекция точки;

(+) невидимая проекция точки (в скобках).