Методы криптоанализа блочных шифров

Метод грубой силы. Метод грубой силы {brute-force attack) предполагает перебор всех возможных вариантов ключа шифрования до нахождения искомого ключа. Для ключа длиной п битов существует 2″ различных вариантов ключа. В процессе перебора всех возможных ключей (от 0 до 2″ - 1 в числовом выражении) обязательно будет найден ключ шифрования, причем такой поиск потребует в среднем 2″ /2, т. е. 2″ ¹ тестовых операций шифрования.

Критерий корректности найденного ключа: результат расшифровки известной криптограммы должен совпасть с соответствующим известным открытым текстом. Этот критерий позволяет однозначно идентифицировать ключ и требует наличия хотя бы одной пары «открытый текст — шифротекст».

Несколько сложнее определить истинный ключ, если атака осуществляется при наличии только шифротекста. В этом случае требуется какая-либо дополнительная информация об открытом тексте, например:

• • если сообщение является осмысленным текстом на естественном языке, то его длина должна превышать расстояние единственности шифра, т. е. позволять однозначное расшифрование криптограммы в осмысленный текст. Если сообщение короче, то при полном переборе ключей может быть получено несколько осмысленных открытых текстов и, соответственно, несколько ключей, каждый из которых является правдоподобным кандидатом в искомые ключи. Если невозможен перехват дополнительных шифротекстов, зашифрованных на том же ключе, нельзя определить, какой открытый текст (и ключ) является искомым, если это не ясно из контекста;
• • если зашифрованы двоичные данные, то необходимо знать какие-либо их особенные характеристики или свойства, например формат файла, предполагающий наличие специфических заголовков;
• • часто в зашифрованный файл внедряется контрольная сумма открытого текста для проверки его целостности после расшифровки. Такая контрольная сумма может быть идеальным эталоном при криптоанализе, позволяющим однозначно определить истинный ключ.

Метод грубой силы неэффективен при достаточно большой длине ключа. При этом увеличение длины ключа на 1 бит увеличивает мощность ключевого пространства (возможное число вариантов ключа), а значит и среднее время атаки, в два раза.

Существуют методы улучшения атаки на основе грубой силы:

• • распараллеливание перебора, когда каждый из участников атаки испытывает некоторое подмножество ключей;
• • использование специализированных устройств (например, в 1995 г. была опубликована информация о специальной микросхеме ORCA компании AT&T, способной осуществить перебор до 30 млн ключей алгоритма DES в секунду).

Понятно, что с развитием вычислительной техники скорость перебора возрастает, а его стоимость снижается. Поэтому требования к размерам ключа постоянно возрастают. Например, в 1995 г. был рекомендован 90-битный размер ключа в качестве абсолютно безопасного с 20-летним запасом. Сейчас для алгоритмов симметричного блочного шифрования рекомендовано использование 128-битных ключей, что считается безопасным примерно с 80-летним запасом.

Потеря стойкости и попытки усиления существующих шифров. Закон Мура (Moore) является оценкой развития вычислительной техники во времени. В базовом варианте он гласит, что для заданной стоимости (в широком смысле, включая энергопотребление, производство оборудования, износ, стоимость хранения и т. д.) вычислительная мощность увеличивается в восемь раз каждые три года. Говоря более точно, можно сказать, что через каждые три года технологические достижения позволяют разместить в четыре раза больше логических элементов в микросхеме заданной стоимости, одновременно ускоряя ее быстродействие в два раза. Закон Мура подтверждался на практике в течение последних 15 лет^[1].

Увеличение вычислительной мощности неизбежно приводит к снижению надежности систем шифрования.

Если закон Мура будет продолжать выполняться, то для сохранения существующей практической стойкости симметричных шифров к длине ключа следует добавлять три бита каждые три года (три бита дает увеличение возможных вариантов ключей в восемь раз: 2 * = 8). Иными словами, симметричные схемы шифрования теряют три бита стойкости за три года либо один бит за год.

Уменьшение стойкости используемых криптосистем во времени отражено на рис. 2.28. Симметричные шифры теряют один бит безопасности в год. Хэш-функции и схемы, основанные на эллиптических кривых, теряют два бита безопасности в год. RSA-схемы теряют 30 бит безопасности в год.

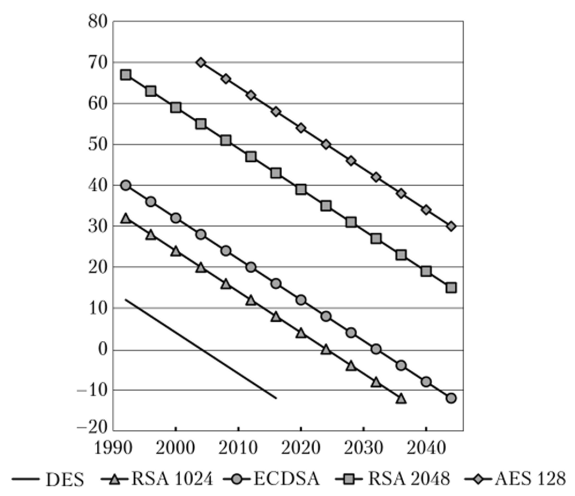
Рис. 2.28. Снижение стойкости криптографических алгоритмов^[2]

Повышение стойкости шифрования обеспечивается на основе двух основных подходов:

• 1) экстенсивный подход — базируется на модификации существующих алгоритмов шифрования в сторону увеличения длины ключей;
• 2) интенсивный подход — базируется на принципиальной смене самого алгоритма шифрования.

Во многих случаях делается попытка усилить существующие и хорошо зарекомендовавшие себя ранее, но устаревшие в силу малой длины ключа алгоритмы шифрования, например алгоритм DES, за счет многократного шифрования на разных ключах. Так появились варианты «двойного» и «тройного» DES. Двойная схема шифрования DES оказалась подверженной криптоанализу методом «встреча посередине» и не смогла намного повысить стойкость исходного DES.

На практике наибольшее распространение получил тройной DES (Triple DES, 3DES) с тремя независимыми ключами (рис. 2.29), обладающий доста;

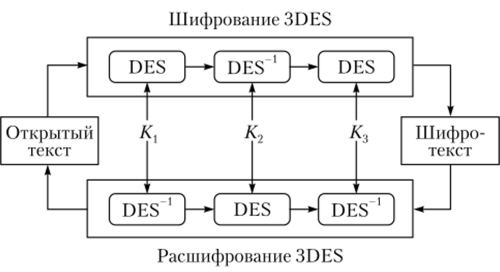
Рис. 2.29. Алгоритм тройного DES.

точной стойкостью. Такая схема шифрования называется EDE {Encrypt — Decrypt — Encrypt) — «зашифрование — расшифрование — зашифрование».

Если все три подключа 3DES независимы (ключ алгоритма имеет длину 168 бит), то применима атака на связанных ключах, которая требует от 2⁵⁶ до 2⁷² операций шифрования. Данная атака достаточно сложна в реализации, поэтому она не повлияла на распространенность алгоритма.

Кроме того, был предложен вариант трехключевого тройного DES со 112-битным ключом шифрования (ТЕМК — Triple Encryption with Minimum Key). В данной схеме 112-битный ключ шифрования К = (&_½, k_2/2) расширяется в три подключа Triple DES следующим образом:

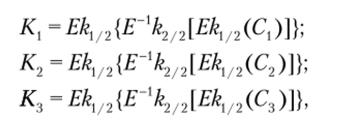
где C_v С₂и С₃ — несекретные константы; Е — процедура шифрования DES; Е~^{ — процедура расшифрования DES. Интересно, что данный алгоритм не подвержен атаке, характерной для трехключевого 3DES с тремя независимыми подключами.

Следует также иметь в виду, что многократное шифрование значительно снижает скорость шифрования и расшифрования данных.

Существует множество способов объединять блочные алгоритмы для получения новых алгоритмов^[3]. Стимулом создавать подобные схемы является желание повысить безопасность с использованием проверенных временем средств, не тратя сил на разработку нового алгоритма.

Идея многократного шифрования для случая разных шифров заключается в их последовательном использовании (cascading), когда производится шифрование сначала алгоритмом А и ключом К_л, а затем еще раз алгоритмом В и ключом К_в. Данную идею можно распространить и на большее количество алгоритмов и ключей.

Показано, что последовательное шифрование взломать, по крайней мере, не легче, чем самый сильный из шифров последовательности, но в основе этих результатов лежат некоторые несформулированные предположения. Ключи для каждого алгоритма последовательности должны быть независимыми.

Существует другой способ объединить несколько блочных алгоритмов, безопасность которого гарантированно будет, по крайней мере, не меньше, чем безопасность обоих алгоритмов. Для двух алгоритмов шифрования и двух независимых ключей:

• 1) генерируется строка случайных битов R того же размера, что и сообщение X;
• 2) R шифруется первым алгоритмом;
• 3) формируется строка X © R, которая затем шифруется вторым алгоритмом;
• 4) шифротекст сообщения является объединением (конкатенацией) результатов этапов (2) и (3).

При условии, что строка битов действительно случайна, этот метод накладывает на X случайную гамму (шифрует сообщение с помощью одноразового блокнота), при этом содержимое гаммы и получившееся сообщение шифруются каждым из двух алгоритмов. Поскольку и то и другое необходимо для восстановления сообщения X, криптоаналитику придется взламывать оба алгоритма. Недостатком является удвоение размера шифротекста по сравнению с исходным открытым текстом.

Этот метод можно расширить для нескольких алгоритмов, но добавление каждого алгоритма увеличивает размер шифротекста.

Метод «встреча посередине». Любые методы, способные вскрыть алгоритм шифрования быстрее, чем полный перебор ключей, эксплуатируют те или иные конструктивные недостатки алгоритма или его реализации. Атака «встреча посередине» позволяет вскрывать любой алгоритм шифрования, представляющий собой двойное шифрование с помощью какого-либо «одинарного» алгоритма.

Атака «встреча посередине» была изобретена в 1981 г. Р. Мерклем (Ralf С. Merkle) и М. Хеллманом (Martin Е. Heilman) в применении к алгоритму Double DES (двойной DES — рис. 2.30). Кроме того, эта атака в более сложном варианте применима к одному из вариантов тройного DES (Triple DES).

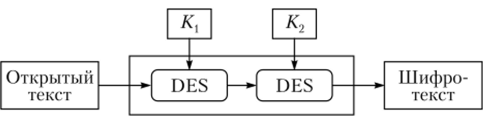
Рис. 2.30. Алгоритм двойного DES.

Ключи К, и К., алгоритма Double DES представляют собой 56-битные половины 112-битного ключа.

Атака методом «встреча посередине» является атакой на основе известных открытых текстов.

Пусть известна пара «открытый текст — шифротекст»: А, — F,. Криптоаналитик должен выполнить следующую последовательность действий (рис. 2.31):

• • выполняется шифрование DES Е_кх(Х_{) на всем ключевом пространстве {К} (Jkx = 0, 1,…, 2⁵⁶ — 1), результаты записываются в таблицу;
• • производится расшифровывание DES К (F,) также на всем ключевом пространстве {К} (ky = 0, 1,…, 2⁵⁶ — 1). Результаты расшифровки сравниваются с таблицей шифрования;

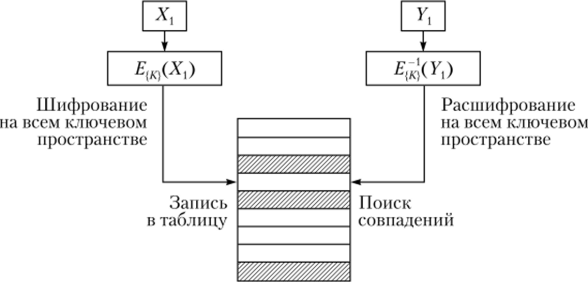
Рис. 2.31. Схема проведения атаки «встреча посередине».

• если какой-либо результат расшифровки У, совпал с одним из результатов шифрования Х_х, то можно предположить, что нужный ключ найден, т. е. соответствующие значения ключей кх = K_v ky = К₂.

Может быть получено достаточно много таких совпадений — порядка 2™ для Double DES. Для уточнения истинного значения ключа требуется наличие еще одной пары «открытый текст — шифротекст»: Х₂ — У₂. Эта пара используется гак же, как и первая, но теперь перебор вариантов ключей kx и ky осуществляется только по уже отобранным значениям ключей, ранее давшим совпадения. В результате будет найден верный ключ. Вероятность повторного совпадения крайне мала — порядка 2^-16 (Double DES), в этом случае может быть использована третья пара: Х._л — У₃.

В результате применения атаки «встреча посередине» сложность вычисления ключа Double DES всего в два раза выше, чем полный перебор ключей обычного DES, что несравнимо меньше полного перебора вариантов двойного ключа (2¹¹²).

Атака «встреча посередине» применима, но малоэффективна для других более современных алгоритмов блочного шифрования. Например, она позволяет:

• • вычислить 192-битовый ключ алгоритма DEAL за 2¹⁶⁶ тестовых операций, а 256-битный ключ DEAL — за 2²²² тестовых операций;
• • вычислить 256-битный ключ SAFER+ за 2²⁴⁰ тестовых операций.

Атаки методами «грубой силы» и «встреча посередине» нередко используются в комбинации с другими атаками, а также для оценки запаса криптостойкости модифицированных версий алгоритмов и алгоритмов с усеченным количеством раундов.

Дифференциальный криптоанализ. Классический дифференциальный криптоанализ. Этот метод предложен в 1990 г. израильскими криптологами Э. Бихамом (Eli Biham) и Э. Шамиром (Adi Shamir) для вскрытия DES.

Метод дифференциального криптоанализа основан на анализе пар открытых текстов с определенными различиями, называемыми разностью (difference), и соответствующих им закрытых текстов. При анализе алгоритмов разность текстов А может быть определена по-разному. Для DES разность открытых текстов Х_х и Х₂ определяется как операция побитового XOR этих текстов: А = Х_х ® Х₂. Метод основан па предположении о существовании определенных разностей на выходе алгоритма шифрования, которые имеют повышенные или, наоборот, пониженные вероятности возникновения (т.е. отличающиеся от ½).

На основе различий в получившихся шифротекстах различным ключам присваиваются разные вероятности. В процессе дальнейшего анализа следующих пар шифротекстов один из ключей станет наиболее вероятным. Это и есть правильный ключ. Задачей дифференциального криптоанализа является нахождение таких разностей исходных текстов АХ и последовательностей раундовых ключей K_v K_v …, К_г, чтобы разность выходных текстов (шифротекстов) AYимела как можно большую вероятность.

Анализ начинают с исследования однораундового алгоритма, затем переходят к алгоритмам с большим числом раундов. Для этого используют характеристики — разности открытых текстов, которые с высокой вероятностью вызывают определенные разности в получаемых шифротекстах. На сегодняшний день неизвестно универсальных алгоритмов поиска характеристик с высокой вероятностью для разных алгоритмов шифрования. Поэтому поиск характеристик является в большой степени творческой задачей.

Дифференциальный криптоанализ часто используют для определения некоторого фрагмента ключа, что сужает область возможных ключей, а остальные биты ключа подбирают методом грубой силы (полным перебором).

Дифференциальный криптоанализ требует выбора открытых текстов и позволяет вскрывать:

• • алгоритм DES и другие алгоритмы с усеченным числом раундов;
• • алгоритм RC2 при наличии 2⁵⁹ выбранных текстов;
• • основной вариант алгоритма RC5 (RC5−32/12/16) при наличии 2^м выбранных текстов, некоторые другие варианты RC5;
• • «ускоренный» вариант алгоритма ICE — Thin-ICE при наличии 2²⁷ выбранных текстов;
• • один из вариантов алгоритма DES — Generalized DES (GDES) с 16 раундами и размером блока 256 бит — при наличии всего шести выбранных открытых текстов. Некоторые другие варианты DES (DESX, DES с независимыми подключами, s²DES и др.) также подвержены дифференциальному криптоанализу.

Существуют различные методы (бумеранга, невозможных дифференциалов и др.), являющиеся развитием классического дифференциального криптоанализа.

Метод бумеранга. Метод предложен в 1999 г., является усилением дифференциального криптоанализа и состоит в использовании квартета (т.е. четырех вместо двух) различающихся открытых текстов и соответствующих им шифротекстов, связанных специальными соотношениями (рис. 2.32).

Метод заключается в следующем:

^предполагается, что алгоритм шифрования можно логически разделить на две примерно равные по трудоемкости части (например, г-раундовый алгоритм со сходной структурой раундов можно разделить на две части по г/2 раундов каждая). Обозначим выделенные части шифрования как ?½ и ?2/2 соответственно;

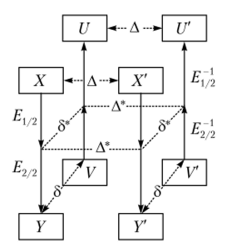
Рис. 232. Схема метода бумеранга.

• 2) для формирования квартета выбирают два открытых текста X и X', разность которых составляет Д. В результате шифрования этих текстов процедурой ?½ будет получена разность Д*;
• 3) продолжив шифрование процедурой ?2/2, можно получить два шифротекста: Y и У';
• 4) полученные шифротексты У и У' используются для выбора двух других шифротекстов V и V, имеющих с ними определенную разность 5;
• 5) затем формирование квартета продолжается в обратную сторону (откуда и пошло название метода) путем расшифрования V и V процедурой? '2/2, что позволяет получить разность 8*;
• 6) окончательная расшифровка V и V 'процедурой? 4/2 позволяет получить открытые тексты U и U', разность между которыми полностью совпадает с разностью между исходными текстами квартета X и X', т. е. равна Д.

Метод бумеранга позволяет атаковать некоторые из алгоритмов, стойких к классическому дифференциальному криптоанализу, а также в ряде случаев — существенно сократить объем требуемых для анализа данных. Вместе с тем, метод бумеранга представляет собой атаку с адаптивным выбором открытых текстов и шифротекстов, т. е. атаку, которую сложнее всего реализовать на практике.

Метод бумеранга применим к достаточно большому числу известных алгоритмов шифрования, в том числе и к некоторым алгоритмам — участникам конкурса AES: CAST-256, MARS и Serpent (два последних — с усеченным числом раундов).

Метод невозможных дифференциалов. Метод предложен в 1998 г., представляет собой принципиально новый вариант дифференциального криптоанализа, использующий так называемые невозможные дифференциалы (impossible differentials), и фактически является дифференциальным криптоанализом «от противного»:

• • выбирается нужное количество пар открытых текстов с требуемой разностью и соответствующих им шифротекстов;
• • выполнятся анализ, в рамках которого все варианты ключа шифрования, приводящие к дифференциалам с нулевой (или минимальной) вероятностью, считаются неверными и отбрасываются;
• • в результате остается единственный возможный вариант ключа или некоторое подмножество ключевого пространства, не приводящее к невозможным дифференциалам. В случае не единственного ключа может быть использован полный перебор, но оставшемуся подмножеству для нахождения верного ключа.

Метод невозможных дифференциалов применим для вскрытия усеченных, но количеству раундов версий таких известных алгоритмов шифрования, как IDEA Khufu и Khafre, Skipjack, MISTY и KASUMI.

Линейный криптоанализ. Линейный криптоанализ был впервые применен к алгоритму DES в 1993 г., а затем распространился и на другие алгоритмы. Линейный криптоанализ основан на поиске линейной аппроксимации между исходным и зашифрованным текстом. Смысл линейного криптоанализа состоит в нахождении соотношений вида.

где Х_пУ Y_n, К_п — п-е биты открытого текста, шифротекста и ключа соответственно.

Для произвольно выбранных битов открытого текста, шифротекста и ключа вероятность того, что такое соотношение будет выполняться, составляет около ½ (Р «½). Если криптоаналитику удастся найти такие биты, при которых вероятность существенно отличается от ½, это может быть использовано для вскрытия алгоритма.

Сначала производится поиск однораундового соотношения (например, рис. 2.33 для алгоритма DES), затем делается попытка распространить его на большее количество раундов. Существуют и алгоритмы поиска полезных соотношений.

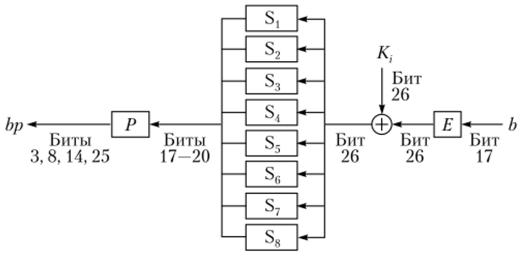
Рис. 2.33. Наиболее эффективное однораундовое соотношение алгоритма DES.

Соотношение, изображенное графически на рис. 2.33, записывается как.

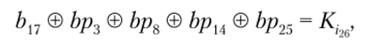
где i — номер раунда.

В отличие от дифференциального криптоанализа, требующего выбранных открытых текстов, для линейного криптоанализа достаточно известных открытых текстов, что существенно увеличивает область практического применения этого метода.

Линейный криптоанализ имеет одно весьма полезное свойство: при определенных обстоятельствах линейное соотношение может быть преобразовано к виду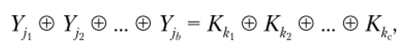

что позволяет исключить необходимость знания открытого текста и проводить атаку только на основании известного шифротекста.

Например, описана подобная атака на полнораундовый DES, которая работает при допущении, что исходное сообщение — осмысленный текст на английском языке в ASCII-кодировке. Для этой атаки требуется порядка 2^ шифротекстов.

Помимо DES, линейный криптоанализ действует против:

• • алгоритма RC5 в случае, если искомый ключ попадает в класс слабых ключей;
• • алгоритмов NUSH и Noekeon (участники европейского конкурса криптоалгоритмов NESSIE);
• • некоторых вариантов DES (DESX, DES с независимыми подключами, Biham-DES).

Основным достоинством линейного криптоанализа, по сравнению с дифференциальным, является отсутствие необходимости выбора открытых текстов, что делает его более применимым на практике. Следует отметить, что трудоемкость обоих методов существенно растет с увеличением числа раундов алгоритма шифрования. Применяется также объединение методов линейного и дифференциального криптоанализа (линейно-дифференциальный криптоанализ).

Слайдовая атака. Линейный и дифференциальный криптоанализ становится неэффективным при большом числе раундов шифрования. В этом случае каждый добавленный раунд требует экспоненциального роста усилий атакующего.

С ростом производительности (скорости вычислений) современных компьютерных систем проявляется тенденция к увеличению числа раундов шифрования (например, RC6 — 20, ГОСТ 28 147–89, MARS, SERPENT — 32, CAST, 3DES — 48 раундов). Таким образом, становится актуальным поиск новых методов анализа, не зависящих от числа раундов в алгоритме шифрования. К таким методам относится слайдовая атака (скользящая, сдвиговая атака, slide attacks), применимая ко всем алгоритмам блочного шифрования. Слайдовая атака использует степень самоподобия функции преобразования алгоритма шифрования, т. е. применение одной и той же криптографической Е-функции, зависящей от одного и того же подключа в каждом раунде шифрования. В зависимости от структуры алгоритма шифрования слайдовая атака может использовать как слабость процедуры формирования подключей, так и более общие структурные свойства шифра.

Обычная слайдовая атака рассчитана на анализ криптоалгоритмов, состоящих из г раундов, каждый из которых осуществляет Е-преобразование входного текста, зависящее от одного и того же значения ключа К (значения всех раундовых ключей одинаковы).

Идея слайдовой атаки заключается в том, что можно сопоставить один процесс зашифрования с другим таким образом, что один из процессов будет «отставать» от другого на один раунд (рис. 2.34).

Пусть Х₀ и Х'₀ — некоторые открытые тексты, в процессе их шифрования Xj = F (Xj_,), Х'= F (X'_ j), j =1,2,…, г. Если имеется некоторая пара значений, такая что, Х'₀ = X_v то и для любого j выполняется Xj__x = X_jy поскольку Xj = = F (X-_ j) = F (Xj) = X _{+ 1}. Значит, и X[__x = X_r. Обозначим входы шифрования как X и Х выходы — как Y и Y. Тогда для слайдового процесса X' = Е (Х) будет выполнено условие Y = Е (Y).

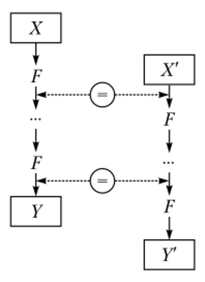
Рис. 234. Схема обычной слайдовой атаки Пара открытых текстов и соответствующих им шифротекстов (X, У) (X', У') называется слайдовой парой в том случае, если выполнены условия F (X)=X' иЕ (У) = Г.

Слайдовая атака проходит следующим образом. Получают пары «открытый текст — шифротекст» (X, У,) с помощью одного и того же ключа, среди которых ожидают найти хотя бы одну слайдовую пару. После того как слайдовая пара найдена, могут быть определены некоторые биты ключа. Для выяснения оставшихся битов секретного ключа следует определить следующую слайдовую пару и с ее помощью провести анализ. Таким образом, для полного определения секретного ключа достаточно найти всего несколько слайдовых пар.

В случае, когда речь идет об алгоритмах шифрования, построенных на схеме Фейстеля, раундовая функция преобразует только половину входного сообщения. Поэтому условие F (X) = X' можно легко проверить, сравнив правую часть сообщения X и левую часть сообщения X'. Таким образом, сложность атаки может быть снижена до 2^п/2 открытых текстов, где п — длина входного блока алгоритма шифрования.

Для сети Фейстеля условие нахождения потенциальной слайдовой пары может быть сформулировано следующим образом: (X, У) образует слайдовую пару совместно с (X', У'), если правые половины X и У' равны, соответственно, левым половинам X' и У: X R = Х' Ь, Y'_R = Y L (рис. 2.35).

Если существует возможность выбора открытых текстов, то для сети Фейстеля сложность анализа может быть снижена до 2^Я/4 открытых текстов. В этом случае выбирается произвольное я/2-битовое значением, затем подбирается массив открытых текстов X = (х, g), которые будут различаться только случайно выбранной правой частью g_f, и массив текстов Х_/ = (g_;, х), которые будут различаться только случайной левой частью g.

Слайдовые атаки применимы также для алгоритмов, в которых функция формирования подключей периодична, т. е. один и тот же подключ повторяется через равное количество раундов. Известны эффективные слайдовые атаки для сети Фейстеля с двухраундовым самоподобием:

• • слайдовая атака с использованием дополнений, которая основана на отборе открытых текстов, различия которых компенсируют различие подключей;
• • слайдовая атака с петлей, основанная на сопоставлении процессов шифрования и расшифровки.

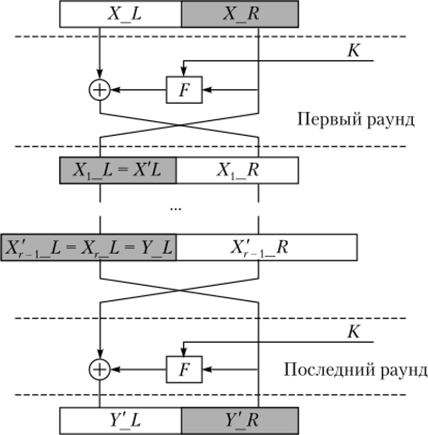
Рис. 2.35. Выбор слайдовой пары для сети Фейстеля

Комбинация этих методов позволяет проводить атаки на сети Фейстеля с 4-раундовым самоподобием.

Самый простой вид слайдовой атаки обычно легко пресечь, избавившись от самоподобия в алгоритме шифрования. Более сложные варианты предполагают и более сложный анализ, однако против них гораздо сложнее защититься.

С помощью слайдовой атаки был полностью раскрыт алгоритм TREYFER, предложенный в 1997 г. для применения в смарт-картах и других устройствах с ограниченными ресурсами. Слайдовая атака применима к модифицированным (но не полноценным) вариантам DES (2K-DES) и Blowfish. Усиленные варианты слайдовой атаки использованы для взлома нескольких вариантов алгоритма DES, а также усеченного модифицированного алгоритма ГОСТ 28 147–89.

Атака на связанных ключах. Классическая атака на связанных ключах во многом похожа на слайдовую атаку. Основное различие состоит в том, что если в слайдовой атаке используют два открытых текста X и Х связанных между собой соотношением X' = F (X, /С,), где F — функция раундового преобразования, К, — ключ первого раунда, то атака на связанных ключах использует весьма похожее соотношение, только между ключами.

Пусть искомый ключ шифрования К в результате его обработки процедурой расширения ключа G (K) дает следующую последовательность подключей:

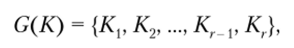
где г — количество раундов алгоритма шифрования.

Предположим также, что есть ключ К расширение которого дает последовательность раундовых ключей, аналогичную предыдущей, но с циклическим сдвигом на одну позицию (рис. 2.36):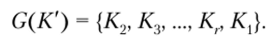

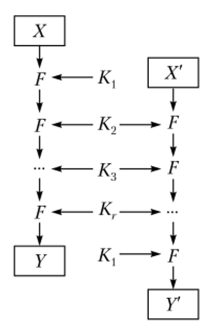
Рис. 236. Соотношение раундовых ключей в классической атаке на связанных ключах Тогда возможна атака, позволяющая отыскать раундовый ключ К_х при наличии 2″ ^/2 пар «открытый текст — шифротекст», зашифрованных на первом ключе К, и 2″ ^/2 пар «открытый текст — шифротекст», зашифрованных на втором ключе К'. При этом, согласно парадоксу дней рождения, потребуется анализ в среднем не более 2^и/2+1 текстов.

В зависимости от структуры самого алгоритма трудоемкость может быть значительно ниже (в частности, для алгоритмов, построенных на сбалансированной сети Фейстеля).

Атака на связанных ключах долгое время считалась мощной, но сугубо теоретической. Сейчас многие эксперты считают, что атаки на связанных ключах могут иметь практическое применение. В любом случае атака должна учитываться при разработке и реализации алгоритмов шифрования.

Атаке на связанных ключах подвержен алгоритм LOKI версий 89 и 91, имеющий чрезмерно простую процедуру расширения ключа. Эта атака была применена также к одному из вариантов шифра Lucifer, другой вариант этой атаки был реализован для шифра SAFER К-64.

Возможные проблемы процедуры расширения ключа. Существуют и другие потенциальные уязвимости, вносимые в алгоритм шифрования неудачно спроектированной процедурой расширения ключа:

• • нестойкость к атакам «встреча посередине», эксплуатирующим тот факт, что первая часть шифрующих преобразований использует иной набор битов ключа, нежели вторая часть;
• • наличие слабых ключей — ключей, зашифрование с использованием которых эквивалентно расшифровыванию или обладает другими характеристиками, существенно упрощающими вскрытие;
• • наличие эквивалентных ключей — различных ключей, дающих один и тот же результат шифрования на некотором подмножестве открытых текстов;
• • наличие классов ключей, позволяющих криптоаналитику легко определить подмножество ключевого пространства, которому принадлежит искомый ключ, и, соответственно, уменьшить область полного перебора.

Атаки, использующие утечки по побочным каналам. Данный вид атак, в отличие от рассмотренных ранее, эксплуатирует не уязвимости структуры шифра, а нацелены на его программные или аппаратные реализации. Успех этих атак во многом зависит от того, насколько реализация алгоритма в программном или аппаратном шифраторе учитывает возможность таких атак и защищена от побочных утечек информации. Наиболее часто атакуемыми оказываются криптографические смарт-карты, т. е. достаточно низкоскоростные шифраторы, работающие в условиях ограниченных ресурсов.

Полученная информация может использоваться криптоаналитиком в контексте других атак, например для сужения области возможных значений ключа шифрования.

Все атаки, использующие утечку данных по побочным каналам {sidechannel attacks), условно разделяют на две категории: пассивная прослушка и атаки на основе сбоев (fault attacks).

Пассивные атаки — пассивная прослушка шифратора с целью получения нужной информации:

• • атаки по времени выполнения (используют тот факт, что на некоторых аппаратных платформах для выполнения определенных операций требуется различное количество тактов процессора, что позволяет сделать предположения о значении того или иного фрагмента ключа);
• • атаки по потребляемой мощности (высокоточный замер мощности шифратора, потребляемой при выполнении различных операций с целью получения информации о выполняемых операциях и ключе шифрования). Усилением этой атаки является дифференциальный криптоанализ по потребляемой мощности;
• • атаки, использующие высокоточные измерения электромагнитного излучения шифратора (простой и дифференциальный анализ электромагнитного излучения). В 2000 г. этот метод был применен для атаки на криптографические смарт-карты, реализующие алгоритмы DES, RSA и COMF128. Во всех трех случаях атака этим методом позволила вычислить значения ключей шифрования;
• • атаки, основанные на сообщениях об ошибках, — анализ сообщений, выдаваемых шифратором в случае ошибочных ситуаций при расшифровывании, например при попытке расшифровки неверным ключом.

Активные атаки — атаки, для проведения которых производятся различные воздействия на шифратор с целью получения дополнительной информации во время сбоев шифратора — атаки на основе сбоев:

• • изменение напряжения питания шифратора, существенно превосходящее допустимые пределы;
• • изменение тактовой частоты шифратора, также выходящее за допустимые пределы;
• • высокочастотное облучение шифратора с помощью лазера, ультрафиолетового, рентгеновского или какого-либо другого излучения;
• • высокочастотное наведение электромагнитного поля или локальный нагрев определенной области шифратора;
• • внесение изменений в конструкцию шифратора, например нарушение определенных электрических контактов.

Атаки на основе сбоев классифицируют также, но тому, насколько атакующий может контролировать следующие факторы:

• • местоположение сбоя (например, конкретный бит обрабатываемых данных);
• • время возникновения сбоя (например, номер конкретного раунда шифрования);
• • количество битов, подверженных сбою;
• • вид сбоя: инверсия значения бита или его сброс.

Дифференциальный криптоанализ на основе сбоев, предложенный в 1996 г., требует несравнимо меньше данных, чем «классический» дифференциальный анализ. Несмотря на то, что модель атаки является достаточно строгой и сложно реализуется на практике, этот метод является весьма мощным и применим ко многим алгоритмам блочного шифрования (IDEA RC5, FEAL, Khufu и Khafre, Blowfish, DES, Triple DES, DES с независимыми подключами), несколько видов атак данным методом предложено и против AES.

К сожалению, нет универсального метода противодействия описанным активным атакам, однако можно значительно усложнить проведение атак на основе сбоев аппаратного шифратора:

• • внедрение в шифратор детекторов различных воздействий, которые при обнаружении воздействия осуществляют блокировку шифратора;
• • пассивное экранирование устройства, устранение которого приводило бы к выходу шифратора из строя;
• • дублирование вычислений со сравнением результатов.

Методы защиты программных шифраторов:

• • использование контрольных сумм фрагментов данных для периодической проверки их целостности в процессе вычислений;
• • дублирование вычислений со сравнением результатов;
• • внедрение в программу случайных избыточных вычислений.

Подобные методы приводят к удорожанию шифратора и (или) снижению его быстродействия, однако повышают его безопасность.

• [1] Pomin Т. Длина ключа и его полный перебор: пер. с фр. Cybervlad. URL: http://cybendad.net/faq-cle/index.html#toc
• [2] Network Security. V2004. Issue 12. Dec. 2004. P. 6—11.
• [3] Жданов О. Н., Золотарев В. В. Методы и средства криптографической защиты информации.