Ряды функций. 
Введение в теорию функций комплексного переменного

Понятие равномерно сходящегося ряда.

Пусть имеем ряд:

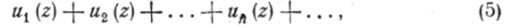
все члены которого суть однозначные функции комплексного переменного z, определённые в некоторой области О; предположим, что этот ряд сходится во всякой точке z области О. В этом случае сумма 5 ряда (5) будет однозначно определена в каждой точке z области G и, следовательно, будет представлять однозначную функцию s (z) в области О. Предположим, что все члены сходящегося ряда (5) суть непрерывные функции в области G; тогда возникает вопрос: не будет ли и сумма ряда непрерывной функцией? Легко лать примеры, когда сходящиеся ряды непрерывных функций изображают разрывные функции. Возьмём сначала пример из области действительного переменного. Предполагая образуем ряд, сумма первых п

членов которого s_n (л:) равна х^п. Это будет ряд:

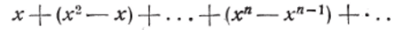
Если 0^.v<^ 1, то s_n(x) = xⁿ стремится к нулю при неограниченном возрастании п если же х=, то ^_я(1) = 1 и lim $_я(1) = 1. Следо;

п -+ 00.

вательно, сумма рассматриваемого ряда s (jc) равна нулю при 0 1.

и равна единице при х=. Итак, сумма s (x) имеет точку разрыва при л: = 1, несмотря на то, что данный ряд сходится в каждой точке отрезка O^jc^I и все его члены — непрерывные функции. Этот пример можно, конечно, рассматривать и с точки зрения комплексного переменного, если заметить, что x = R{z).

В качестве другого примера возьмём ряд:

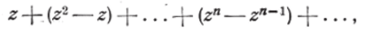
предполагая |z|z= 1. Если |z|п членов s_n(z) = zⁿ стремится к нулю при неограниченном возрастании л, потому что s_n (z) | = | z |^я. Если же z= 1, то s_n( l) s=l, и lim ?_я(1)= 1. Итак, сумма рассматриваемого ряда s (z) равна нулю л-юо во всякой точке z, лежащей внутри круга |z|<^l, и равна единице в точке z= 1 окружности этого круга. Здесь, как и в первом примере, функция $(z) оказывается разрывной при z=l и изображается в виде суммы сходящегося ряда непрерывных функций.

Итак, для того, чтобы сумма сходящегося ряда непрерывных функций была непрерывной функцией, нужно на этот ряд наложить дополнительное ограничение. Таким ограничением может служить условие равномерной сходимости ряда. Обозначая через s_nz) сумму первых п членов данного ряда (5), сходящегося в области О, рассмотрим разность s (z) — s_n(z)_y которая вследствие сходимости ряда стремится к нулю при неограниченном возрастании п для любой точки z области G. Это значит, что выполняется неравенство:

где г — сколь угодно малое положительное число, если п z).

При изменении точки z в области G может случиться, что N (е, z) принимает сколь угодно большие значения. В этом случае нельзя найти такое число 7У=уу (е", начиная с которого выполнялось бы неравенство (6).во всей области G. Другая возможность состоит в том, что N (s, z) для всех точек области G остаётся меньше некоторого числа N = N{b). В этом случае неравенство (6) выполняется для всех рассматриваемых точек z при n^N=N (?) в этом случае говорят, что данный р «д (6) сходится равномерно в области G к функции 5 (z).

Итак, ряд (5), по определению, сходится равномерно в области G к функции s (z), если для всякого сколь угодно малого положительного числа в можно найти такое натуральное число N=N (g), что при всех N выполняется неравенство | s (z) — s_n (z) | <. s* какова бы ни была точка z в области G.

Иными словами, в случае равномерной сходимости ряда его сумму можно аппроксимировать с любой степенью точности е посредством суммы одного и. того же числа п первых членов, принимая n^N= N (z).

В предыдущем примере |s (z) — s_n(z) = zⁿ = z^tt, если |z|<0- Для трго, чтобы выполнялось неравенство |s (z) — s_n (z) | е, нужно.

In —.

потребовать, чтобы было zⁿ откуда п —р Обозначая через.

^|пй m-L.

N (e, z) наибольшее целое число, содержащееся в количестве —г~Г ^ *

• 1пГ-.
• 1*1

мы видим, что неравенство (6) будет выполнено, при n^N (s, z). Когда z стремится к единице, то /V (s, z) стремится к бесконечности, и, следовательно, нельзя указать натуральное число Л/, которое было бы больше, чем УУ (е, z)_y для любого z, z<^. Следовательно, этот ряд не будет равш мерно сходиться в круге | z | 1. Однако, этот ряд будет равномерно сходящимся во всяком круге |z|s^r, г<^1.

В самом деле, так как ln-^^ln —, то.

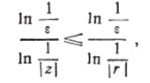
и, следовательно, обозначая через 7V=jV (s) наибольшее натуральное.

1п 4;

число, содержащееся в выражении —р 1, имеем: N(s, z) ^ N= N (e)_t

In —- г

каково бы ни было z, | z | ^ г.