Определение функции полезности

Пусть г — некоторый доходу г е R, где R — множество возможных доходов. Стоит отметить, что элементы множества R не являются обязательно денежными вознаграждениями. Среди примеров таких множеств могут встречаться следующие: множество билетов на различные концерты, множество продуктовых наборов, множество возможных экономических состояний некоторого человека в определенный момент времени в будущем (измеряемых разностью его доходов в будущем и в настоящий момент), множество возможных экономических состояний некоторого государства в определенный момент в будущем (задаваемых размером национального дохода, дохода на душу населения, уровнем безработицы или каким-нибудь другим показателем).

Для любого множества R ЛПР будет иметь предпочтения к тем или иным доходам. В некоторых ситуациях эти предпочтения очевидны (например, в случае с денежными доходами однозначным образом действует правило «чем больше доход, тем он предпочтительнее»), однако в ряде ситуаций, требующих рассмотрения относительного удобства, получаемого от различных факторов (например, не только стоимость билетов на концерт, но и день, время, место и ряд), предпочтения становятся менее ясными. Наиболее сложными примерами принятия решений служат ситуации, когда доходы — это различные состояния экономики и выбор производится не отдельным индивидуумом, а весьма сложным государственным аппаратом.

При сравнении двух доходов r е R и r₂ е R тот факт, что г₂ предпочтительнее г, как было определено в параграфе 14.2, будем обозначать г_х < г₂; через г, ^ г₂ будем обозначать факт их эквивалентности (одинаковой выгодности). Как и ранее, тот факт, что г_х не является более предпочтительным, чем г₂, далее будет обозначаться г_х ^ г₂, что означает по сути, что-либо r_x < г₂, либо г_х ~ г₂. Наконец, по определению, г_х > г₂ обозначает то же самое, что и r₂v и г_х ^ г. у то же самое, что и г₂ < г,. Предполагается, что на основе своих предпочтений среди доходов ЛПР может задать полное упорядочение множества R. Другими словами, на отношение < налагаются следующие два условия.

• 1. Если г_х и г₂ — произвольные доходы из множества R, то верно одно и только одно из следующих соотношений: г_х < г₂, г, > г₂, г, ~ г₂.
• 2. Если r_v г₂ и г₃ — доходы из R> причем г, ;$ г₂ и г₂ ;$ г₃, то г, ;$ г₃.

Наконец, предполагается, что не все доходы из R эквивалентны, т. е. исключается тривиальная ситуация в рамках действующего предположения, что 5₀ < t₀ хотя бы для одной пары 5₀, t₀ е R.

Обратите внимание!

В большинстве практических задач ЛПР не вполне свободно в выборе дохода. Обычно ЛПР может лишь выбрать из некоторого класса возможных распределений вероятностное распределение на R, согласно которому будет определен доход.

Например, в рассмотренной выше ситуации государство не может избрать точно определенное состояние для своей экономики через год, но, опираясь на экономические учреждения и мероприятия, которые можно регулировать, оно задает некое вероятностное распределение на множестве различных возможных состояний экономики.

Обратите внимание!

Для упрощения процесса понимания будем исходить из предположения, что множество R можно определить таким образом, чтобы оно являлось подмножеством т-мерного евклидова пространства R^m для некоторого значения т.

Пусть на множестве R задана a-алгебра Jy подмножеств R. Для любого вероятностного распределения Р на множестве доходов R, подмножества I е $ и интегрируемой функции g на R абстрактный интеграл вида.

jg®dP® можно понимать как интеграл § g®dF®, где F— m-мерная функ;

/ I

ция распределения на множестве R a R" соответствующая вероятностному распределению Р. Математические преобразования подобных интегралов подробно описаны в учебной и научной литературе по теории вероятностей^[1].

Пусть теперь Щ — это класс всех вероятностных распределений Р на R. Предпочтения ЛПР относительно доходов из R ведут к его предпочтениям относительно вероятностных распределений из То есть, если у ЛПР имеется выбор между двумя случайными механизмами, один из которых доставляет доход из R согласно вероятностному распределению Р, а другой — доход из R согласно вероятностному распределению Р₂, то он, вообще говоря, предпочтет один из этих механизмов. Понятие о случайном механизме важно здесь потому, что оно отражает следующее соображение: для сравнения двух вероятностных распределений на R существенны лишь вероятности получения различных доходов, и ЛПР не должно принимать во внимание отдельные события в случайном механизме, реализующем эти вероятности. В ситуации, когда речь идет не о вероятностной неопределенности, а о риске, отношения предпочтения также являются определяющим фактором, влияющим на принятия решений ЛПР. Предпочтения в теории рисков рассматриваются в гл. 15. Сейчас вернемся к изучению класса вероятностных распределений на множестве доходов.

Для обозначения предпочтений среди вероятностных распределений из будем использовать то же символическое обозначение отношений, что и для предпочтения среди доходов. Итак, если Р, е Щ и Р₂ е Щ — два вероятностных распределения, то запись Р_х < Р₂ обозначает, что Р₂ предпочтительнее P_v запись P_t ? Р₂ — что Pj не является более предпочтительным, чем Р₂, и Р, ~ Р₂, когда Р, и Р₂ эквивалентны.

Если г_{ и г₂ — два дохода, причем г_х ^ г₂, то интервал [r_v г₂ определяется как следующее подмножество в R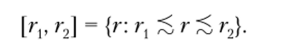

Предположим, что каждый интервал [г, г., принадлежит ст-алгебре 3. Следовательно, для каждого вероятностного распределения Р е Щ определены вероятности P ([r_v г₂]).

Определение

Распределение Р е ^ называется финитным (ограниченным), если существуют доходы г, и г₂, г, ;$ г₂, такие, что P ([r_v г₂)) = 1. Другими словами, распределение финитно, если некоторый интервал [г, г₂] имеет полную меру.

Напомним, что мера является полной, если любое подмножество множества меры нуль является измеримым^[2].

Пусть ty_B обозначает класс всех финитных распределений из Предполагается, что на основе своих предпочтений ЛГ1Р может вполне упорядочить множество Я-V Другими словами, предполагается, что отношение > на множестве обладает такими двумя свойствами.

• 1. Если Pj и Р₂ — два произвольных распределения из ty_B, то справедливо одно и только одно из следующих соотношений: Р, < Р₂, Р, > Р₂, Р, ^ Р₂.
• 2. Если Р, Р₉ и Р₃ — распределения из ty_B, такие, что Р, ^ Р₂ и Р₂ Р₃, то Р ^< Р

Теперь перейдем непосредственно к определению понятия полезности.

Ранее рассматривалось математическое ожидание дискретной случайной величины. Оно является частным случаем более общего (и более подробного в смысле аксиоматики Колмогорова) определения данной числовой характеристики^[3].

Определение

Математическим ожиданием или средним значением случайной величины заданной на вероятностном пространстве (Q, Jy, Р) (где Q — множество элементарных событий, Jy — а-алгебра случайных событий, определенных на этом множестве, Р — счетно-аддитивная мера, определенная на данной о-алгебре), называется число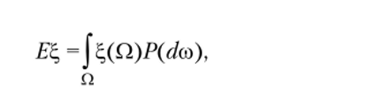

если интеграл, стоящий в правой части, существует.

Перейдем к принятым ранее обозначениям. В качестве прямого следствия из последнего определения получим для всякого распределения Р е и всякой вещественной функции g на множестве Р, что математическое ожидание функции g (если оно существует) относительно распределения Р можно определить следующим образом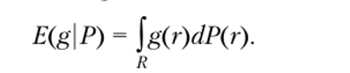

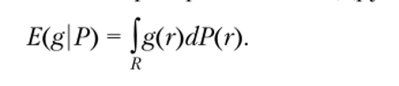
Вещественная функция U, заданная на множестве R, называется функцией полезности (от англ, utility — полезность), если она обладает следующим свойством. Пусть Р, € и Р₂ е ^s4 $ — два распределения, для которых существуют средние (математические ожидания) E (UP_X) и E (UP₂). Тогда Р_{ ? Р₂ в том и только в том случае, когда E (UP_{) < E (UP₂).

Для любого дохода г е R число U® называется полезностью г. Таким образом, одно вероятностное распределение следует предпочесть другому в том и лишь в том случае, когда ожидаемая полезность получаемого дохода при первом распределении больше, чем при втором.

Для всякого распределения Ре и всякой вещественной функции g на множестве R обозначим через E (gP) математическое ожидание функции g (если оно существует) относительно распределения Р. Другими словами,.

Определение

Для всякого распределения Р е $ число E (UP) (в случае, когда это математическое ожидание существует) часто называют просто полезностью Р. Итак, полезность вероятностного распределения — это ожидаемая полезность дохода получаемого при этом распределении. По этой причине предположение о существовании функции полезности часто называют предположением о средней полезности.

Из условий существования функции полезности естественным образом вытекает следующая теорема.

Теорема об ожидаемой полезности

Пусть r_t е R и r₂ е R — два дохода. г, & г₂ тогда и только тогда, когда для функции полезности U® выполнено U (r_{) < U (r₂). При этом всякая функция V® вида V® = aU® + р, где аир — постоянные, а > 0, также является функцией полезности.

Доказательство данной теоремы напрямую следует из определения полезности и общих свойств математического ожидания^[4].

• [1] Боровков Л. Л. Теория вероятностей. М.: Наука, 1986. 432 с.; Севастьянов Б. А. Курс теории вероятностей и математической статистики. М.: Наука, 1982. 256 с.
• [2] Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа.7-е изд. М.: Физматлит, 2004. 572 с.
• [3] Боровков А. А. Указ. соч.
• [4] Де Гроот М. Оптимальные статистические решения. М.: Мир, 1974. 491 с.