Уравнение Ляпунова и критерий Ляпунова устойчивости линейных систем

Рассмотрим линейную систему.

где х — вектор (х € #^п), А — квадратная матрица n-го порядка. Пусть задана квадратичная форма tu (x) = х^гСх. Для того чтобы эта квадратичная форма была равна производной, но времени от квадратичной формы У (х) = х^тВх в силу системы (4.21), т. е. У (х) =-ш (х), матрица В должна удовлетворять матричному уравнению Действительно, производная по времени от квадратичной формы У (х) = х^тВх в силу уравнения (4.21) имеет вид

Отсюда следует, что равенство /(х) = w (x) возможно в том и только том случае, если матрицы В и С удовлетворяют уравнению (4.22), которое называется уравнением Ляпунова. Таким образом, чтобы по заданной квадратичной форме tu (x) = х^тСх найти соответствующую ей квадратичную форму К (х) = х^т?х, нужно решить уравнение Ляпунова.

Исследование уравнения Ляпунова представляет большой интерес, так как это уравнение позволяет найти функцию Ляпунова в виде квадратичной формы по заданной ее производной. Естественно возникает вопрос: когда уравнение Ляпунова имеет решение? Ответ на этот вопрос зависит от того, какие корни имеет характеристическое уравнение системы (4.21).

Теорема 4.14 (теорема о существовании решения уравнения Ляпунова). Если среди корней характеристического уравнения (4.23) нет пари корней, сумма которых равна нулю, т. е. Aj + Xj ф 0 при всех i, j = 1,2,…, п, то при любой симметрической матрице С уравнение Ляпунова имеет единственное решение для неизвестной матрицы В.

Эта теорема может быть доказана с помощью теории операторов [7], и ее доказательство здесь не рассматривается.

Теорема 4.15 (критерий устойчивости Ляпунова линейных систем). Для того чтобы линейная стационарная система (4.21) была асимптотически устойчива, необходимо и достаточно, чтобы для любой отрицательно определенной квадратичной формы w (x) = = х^ТСх существовала положительно определенная квадратичная форма V (x) = х^ТВх такая, что производная по времени от этой функции в силу уравнения системы (4.21) равна заданной квадратичной форме щ (х): У (х) = w (x).

Доказательство. Необходимость. Существование некоторой квадратичной формы У (х) = х^Т Вх, производная от которой по времени равна заданной квадратичной форме, следует из теоремы 4.14. Поэтому достаточно показать, что эта квадратичная форма является положительно определенной функцией.

Пусть система (4.21) устойчива. Тогда ее решение, которое при начальном условии х (0) = х° имеет вид (см. (1.10)) х (?) = е^х⁰, стремится к нулю при t —> оо. Следовательно, и квадратичная форма V (x (?)) —" 0 при? —> оо. Покажем, что квадратичная функция, удовлетворяющая условиям теоремы, является положительно определенной функцией. Допустим противное: в некоторой точке х = х° ф О квадратичная форма К (х°) ^ 0. Тогда в силу того, что.

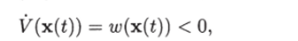
где x (t) = e^Atx°_y функция V (x (t)) при t > 0 отрицательна и убывает с ростом t. А это противоречит тому, что К (х (?)) —> 0 при t —> оо.

Достаточность непосредственно следует из теоремы Ляпунова об асимптотической устойчивости.

Теорема 4.16 (теорема о существовании положительно определенного решения уравнения Ляпунова). Если матрица Л устойчива, т. е. все ее собственные значения имеют отрицательные вещественные части, то, какова бы ни была отрицательно определенная матрица С, уравнение Ляпунова (4.22) имеет единственное решение В, которое является положительно определенной матрицей.

Эта теорема непосредственно вытекает из теорем 4.14 и 4.15.

Теорема 4.17. Если среди корней характеристического уравнения системы (4.21) имеется хотя бы один корень с положительной вещественной частью и сумма никаких пар этих корней не обращается в нуль, то, какова бы ни была положительно определенная функция w (x), найдется квадратичная форма V (x), у которой производная по времени в силу указанного уравнения системы удовлетворяет уравнению 1/(х) = w (x), и в любой окрестности начала координат имеется точка, в которой V(х) принимает положительное значение.

Доказательство. Существование квадратичной формы К (х), удовлетворяющей указанному в теореме уравнению, следует из теоремы 4.14. Покажем, что в любой окрестности начала координат существует точка, в которой V (x) принимает положительное значение.

Квадратичная форма К (^х) не может быть отрицательно определенной, так как в противном случае функция — V (x) удовлетворяла бы условию теоремы Ляпунова об асимптотической устойчивости. В силу указанной причины в любой окрестности начала координат существует точка, где V (x) по крайней мере обращается в нуль. Но так как V'(x) = w (x) > 0, то в любой окрестности такой точки существует точка, где V(х) > 0.

Теорема 4.18. Если среди корней характеристического уравнения системы (4.21) имеется хотя бы один корень с положительной вещественной частью, то, какова бы ни была положительно определенная квадратичная форма w (x), всегда найдутся квадратичная форма V (х) и положительное число, а такие, что производная V (х) в силу указанного уравнения системы удовлетворяет соотношению

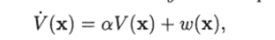
и в любой окрестности начала координат найдется точка, в которой квадратичная форма V(х) принимает положительное значение.

Доказательство. Рассмотрим наряду с (4.21) систему.

Характеристическое уравнение этой системы имеет вид.

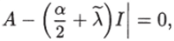
и его корни Ai связаны с корнем Ai характеристического уравнения системы (4.21) соотношением А* = + а/2.

Пусть Ai₀ — корень с положительной вещественной частью. Выберем, а таким, чтобы выполнялись условия:

• 1) из ReAj₀ > 0 следует ReA;₀ > 0;
• 2) А* + А^ ф 0 при всех г и А;.

Условие 1) всегда можно выполнить, выбрав а достаточно малым. Учитывая, что А* + А* = Aj + А* — а, можно выбрать а, не совпадающим ни с одной суммой А* + А*.

Согласно теореме 4.17 для положительно определенной функции найдется квадратичная форма V (x), принимающая в какой-либо точке любой окрестности начала координат положительное значение, и производная по времени этой формы в силу уравнения (4.24) равна w (x):

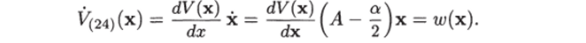
Так как Лх — производная по времени квадратичной формы V (x) в силу уравнения (4.21) и в случае квадратичной формы.

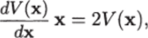
то из последнего соотношения получаем.

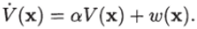
Теорема доказана.