Интегралы с переменным верхним (нижним) пределом. 
Формула Ньютона — Лейбница

Пусть функция/интегрируема на отрезке [а, Ь], х₀ е[а, Ь]. Функция.

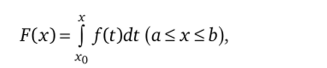
называется интегралом с переменным верхним пределом от функции/ на [а, Ь]. Аналогично вводится понятие интеграла с переменным нижним пределом.

При доказательстве дальнейших теорем нам понадобится следующее свойство определенного интеграла: если функции/и g интегрируемы по Риману на отрезке [а, Ь], причем /(х) > g (x) для любой точки х е [а, Ь],.

ь ь

то J f (x)dx > j g (x)dx. Это свойство немедленно вытекает из определе;

а а

ни я интеграла как предела интегральных сумм и теоремы о предельном переходе в неравенствах (см. параграф 2.1, свойство 2). Обратимся к важнейшим свойствам функции F.

Теорема 1.10. Пусть функция f интегрируема на отрезке Га, Ы,.

Доказательство. Так как / интегрируема на отрезке [а, Ь], то она ограничена на нем. Значит, существует число А > 0, такое что |/(х)| < А Vx€[a, b]. Возьмем произвольную точку хе[а, Ь]. Пусть Ах — действительное число, достаточно малое, чтобы удовлетворять условию х + Axe[a, b] (в случае х = а нам нужно доказать только непрерывность функции F справа, и мы берем Ах > 0, в случае х = Ъ берем Ах < 0). Тогда.

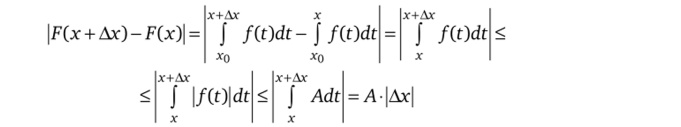
(при этом было использовано свойство 5 из параграфа 2.1). Это означает, что |F (x + Ax)-F (x)| —" 0, т. е. что функция F непрерывна в точке Дг—>о х ее [а, Ь]. Теорема доказана.

Теорема 1.11. Пусть функция / интегрируема на отрезке [а, Ь],.

X

х₀ е [а, Ъ]. Если/ непрерывна в точке % е [a, b], то функция F (x) = J /(t)dt.

*о.

дифференцируема в точке Ъ, и F'(^) = /©.

Доказательство. Выберем произвольное число е > 0. Так как функция /непрерывна в точке ^e[a, b], то существует число 6>0, такое что /(?) — е < /(t) < /(?) + е для любой точки te (^-8,^ + 8). Пусть сначала Ъ, фЪ. Выберем число Ах, 0<�Ах<8, достаточно малое для того, чтобы отрезок [?,?; + Ах] целиком лежал внутри отрезка [а, Ь]. Тогда.

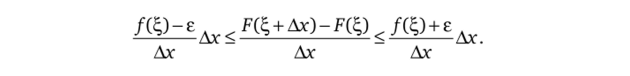
Это означает, что при достаточно малых значениях Ах > 0 число.

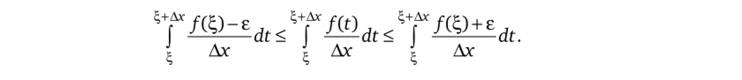
Проинтегрируем последнее неравенство:

F (? + Ax)-F (?), т.

—²-— принадлежит отрезку /(q) — E,/(q) + е .

Ах Пусть теперь 2; Ф а, число Ах принадлежит интервалу (-6,0) и достаточно мало для того, чтобы отрезок [2; + Ах, 2;] принадлежал [а, Ь]. Тогда аналогично предыдущему случаю имеем.

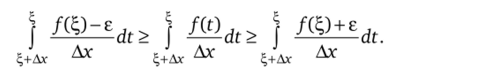
Отсюда после интегрирования получаем, что.

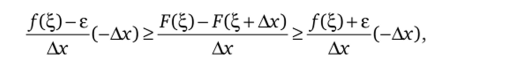
Fit, + Ах)-F (2;) г1.

т. е. снова число —^[1][2]-— лежит на /(q)-e,/(^) + e .

Ах.

F (2: + Ax)-F (2i).

Таким образом, мы доказали, что urn —²-— существует дх—>о Ах и равен (в случае 2; = а доказано существование предела справа, с, s «F (? + Ax)-F (?) j.

в случае q = о — слева). Но по определению пт —²-— = F (q).

дх—>о Ах Теорема доказана.

Следствие. Если функция /непрерывна на отрезке [а, Ь], х₀ е[а, Ь],.

то функция F (x) = J /(t)dt является одной из (точных) первообразных¹/.

х0.

на [а, Ь].

Теорема 1.12. Кусочно-непрерывная^[2] на отрезке [а, Ь] функция f имеет (обобщенную) первообразную^[4] на этом отрезке.

Доказательство. Пусть х_1;…, х^ — точки разрыва функции и.

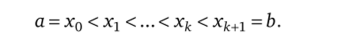
Тогда функция/непрерывна на каждом из интервалов (х^.хД j = = l,…, fc +1, следовательно, на каждом таком интервале существует точная первообразная для/, т. е. функция F_p такая что F'(x) = /(х), х е (Xj_|, Xj). Положим Fj(Xj_!) = Fj (Xj_j +0), Fj (xj) = F_}(x,? -0) и рассмотрим функцию.

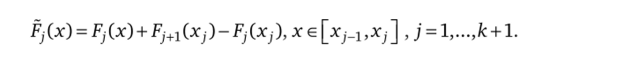
Тогда очевидно, что функция F (x) = F,(x), xe[x_;__1;Xj], j = l,…, fc + l, определена и непрерывна на всем отрезке [а, Ь]. Значит, согласно определению эта функция является обобщенной первообразной для / на [а, Ь].

Теорема 1.13 (формула Ньютона — Лейбница, или основная теорема интегрального исчисления). Пусть функция / непрерывна на отрезке [а, Ь]. Тогда

где Ф —любая из (точных) первообразных функции/на отрезке [а, Ь].

X

Доказательство. Пусть F (x) = J/(t)df. Так как/непрерывна на [а, Ь],.

а

то по следствию из теоремы 1.11 получаем, что F'(x) = f (x) для любого х е [а, Ь]. Поскольку любые две первообразные одной и той же функции могут отличаться только на константу, то для произвольной первообразной Ф функции/на [а, Ь] справедливо соотношение Р'(х) = Ф (лг) + С. Тогда имеем.

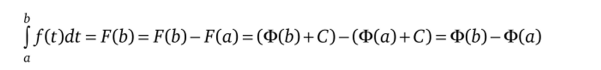
а.

(здесь был использован тот факт, что F (a) = J f (t)dt = 0).

а

Теорема доказана.

Следствие. Производная интеграла с переменным верхним (нижним) пределом находится по правилу.

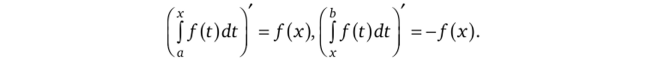
Замечание 1.9. Формула Ньютона — Лейбница верна и в случае, когда Ф — обобщенная первообразная.

Замечание 1.10. В общем случае, когда необходимо продифферен;

vM.

цировать по х интеграл вида J f (t, x) dt, в котором подынтегральная.

<�рМ функция f (t, x) и пределы интегрирования (р (х),|/(х) зависят отх как от параметра, используют формулу Лейбница

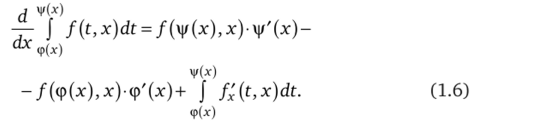
• (при этом функции ф (х), у (х) должны быть дифференцируемы, а функции /(t, х) и fx (t, x) — непрерывны в соответствующих промежутках. Строгое обоснование условий применимости данной формулы изучают позже в разделе «Интегралы, зависящие от параметра»).
• 2

Найти J sgnxdx.

— i.

Решение. Поскольку функция F (х) = |х| является первообразной для подынтегральной функции /(x) = sgnx (в обобщенном смысле: F непрерывна на отрезке [-1,2] и ее производная всюду, за исключением точки х = 0, где функция не дифференцируема, совпадает с/), то, применяя формулу Ньютона — Лейбница, получаем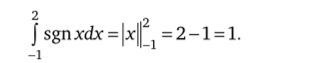

Пример 1.2.

Объяснить, почему формальное применение формулы Ньютона — Лейбница приводит к неверным результатам:

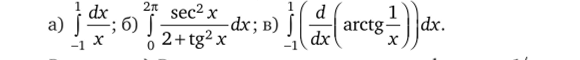
Решение, а) Во-первых, подынтегральная функция 1/х не ограничена на промежутке интегрирования (в окрестности точки х = 0 нарушается необходимое условие интегрируемости), т. е. эта функция не интегрируема на данном отрезке. Кроме того, функция 1п|х|, являющаяся первообразной для подынтегральной функции, разрывна на отрезке [-1,1] (в точке х = 0). Формула Ньютона — Лейбница неприменима.

• 1¹ COS² X
• б) Подынтегральная функция ——— имеет устранимые разрывы в точ-
• 2 + tg² х

к Зк

ках х = — и х = —, принадлежащих промежутку интегрирования. В этих точках функцию можно доопределить до непрерывной значением Л.

поэтому функция интегрируема на [0,2л]. Однако первообразная функцияJ=arctg^-^=-j имеет разрывы 1-го рода в указанных точках. Поэтому формулу Ньютона — Лейбница применять нельзя.

в) Первообразная функция arctg— (и подынтегральная функция тоже) х.

имеет разрыв 1-го рода в точке х = 0. Формула Ньютона —Лейбница неприменима. Для вычисления интеграла следует найти обобщенную первообразную для подынтегральной функции, обладающую свойством непрерывности на отрезке [-1,1].

Замечание 1.11. Необходимо отметить, что интегрируемость функции по Риману на некотором отрезке и существование у нее первообразной на этом отрезке, вообще говоря, не эквивалентны друг другу. Существуют функции, интегрируемые на отрезке, но не имеющие на нем первообразной, и наоборот, функции, имеющие первообразную, но не интегрируемые по Риману (см. задачу 1.54).

• [1] Функция F называется точной первообразной по отношению к функции /на отрезке [а, Ь], если в любой точке х этого отрезка функция F имеет производную F'(x), равную/(х) (на концах отрезка речь идет об односторонних производных).
• [2] Функция/называется кусочно-непрерывной на отрезке [а, Ь], если она непрерывнана этом отрезке всюду за исключением конечного числа точек разрыва 1-го рода х1;…, хк.
• [3] Функция/называется кусочно-непрерывной на отрезке [а, Ь], если она непрерывнана этом отрезке всюду за исключением конечного числа точек разрыва 1-го рода х1;…, хк.
• [4] Функция F называется обобщенной первообразной для функции/на отрезке [а, Ь], если: 1) F непрерывна на [а, Ь]; 2) F'(x) =/(х) в точках непрерывности/.