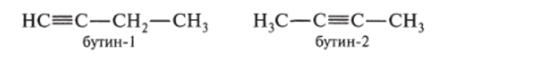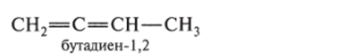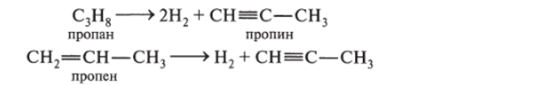Ацетиленовые углеводороды (алкины)

Углеводороды, в молекулах которых содержится одна тройная связь, называются алкинами или ацетиленовыми углеводородами.

В молекулах алкинов между двумя атомами углерода реализуются одна сигмаи две пи-связи, что приводит к увеличению химической активности этих углеводородов по сравнению с олефинами и другими веществами, содержащими двойную связь (одну или несколько). Общая формула алкинов С"Н_2л_₂. Они образуют гомологический ряд:

Название ацетиленовых углеводородов производят от названия алканов, заменяя окончание -ан на -ин. Для ацетиленовых углеводородов характерна изомерия строения углеводородной цепи, положения тройной связи, межклассовая изомерия (алкинам изомерны диеновые углеводороды и циклоалкены, т. е. циклические углеводороды, содержащие одну двойную связь).

Рассмотрим особенности изомерии алкинов на примере веществ с формулой С₄Н₆.

1. Как алкины:

2. Как диеновые: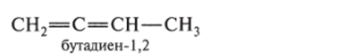

3. Как циклоалкены: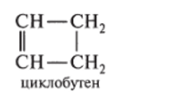

Для С₄Н₆ не характерна изомерия по строению углеводородной цепи.

Алкины, содержащие от 2 до 4 атомов углерода, — газы, от 4 до 15 — жидкости, а остальные — твердые вещества.

Ацетиленовые углеводороды (как и все органические вещества) горят и разлагаются. Они вступают в реакции присоединения (с галогенами, галогеноводородами, водородом), в реакцию Кучерова (см. 12.2), способны к реакциям полимеризации.

Химические свойства алкинов рассмотрены в 13.8 на примере ацетилена. Особенности реакции Кучерова с гомологами этина разобраны в 12.2 на примере взаимодействия пропина с водой, в результате этой реакции всегда получаются кетоны (для всех гомологов, кроме ацетилена).

Способы получения алкинов многообразны. Наибольшее значение имеет дегидрогенизация алканов или алкенов:

Эти реакции протекают при высокой температуре в присутствии никелевого катализатора.

• ? Задания для самостоятельной работы
• 1. Назовите главный признак, характерный для алкинов; напишите их общую формулу.
• 2. Поясните, какое вещество — пропин или пропсн — проявляет большую химическую активность, объясните, почему.
• 3. Назовите классы углеводородов, являющихся изомерными относительно алкинов; напишите формулы изомеров для веществ с эмпирической формулой С₃Н₄.
• 4. Охарактеризуйте особенности и изменения физических свойств в гомологическом ряду алкинов.