Вычисление обратной матрицы методом Жордана — Гаусса

Матрица М ¹ называется обратной для квадратной матрицы М, если справедливо равенство.

где Е — единичная матрица.

Как известно, обратная матрица М^-1 для матрицы М существует тогда и только тогда, когда ее определитель | М отличен от нуля. Поэтому, перед тем как находить обратную матрицу, следует проверить с помощью встроенной функции МОПРЕД (Microsoft Excel), что определитель |М| отличен от нуля.

Если |М| =0, то задача решения не имеет. В дальнейшем будем считать, что |М| ^ 0. При стандартном способе нахождения обратной матрицы к М приписывается единичная матрица, и с полученной длинной матрицей (МЕ) постепенно проводятся преобразования методом Жордана — Гаусса. В результате этих преобразований матрица (М|?) приводится к виду (Е|М^-1). Однако можно немного изменить метод Жордана — Гаусса. Применение этого изменения непосредственно к матрице М, в результате п циклов пересчета, где п — порядок матрицы, приводит к обратной матрице М^-1.

Рассмотрим вышеназванное изменение метода Жордана — Гаусса. При данной «оптимизации» элементы разрешающего столбца пересчитываются по следующим формулам.

Разрешающий элемент заменяется на обратный к нему:

другие элементы разрешающего столбца делятся на разрешающий элемент и берутся с противоположным знаком:

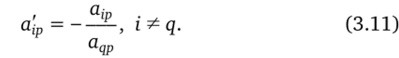
Остальные элементы пересчитываются по старым формулам. Элементы разрешающей строки пересчитываются по формуле.

Элементы, не входящие в разрешающую строку или разрешающий столбец, пересчитываются так:

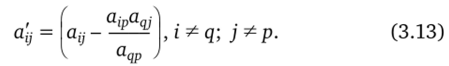
При вычислении обратной матрицы приведенное выше правило выбора разрешающего элемента дополняется тем, что в качестве разрешающих нельзя брать элементы из тех столбцов, в которых на предыдущих шагах находились разрешающие элементы.

Покажем наследующих примерах, как провести вычисление в программе Microsoft Excel.

Пример 3.2.

Найдите обратные матрицы методом Жордана — Гаусса:

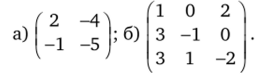
Решение.

а) Откроем файл «Численные методы линейной алгебры». Переименуем лист 2 так: «Вычисление обратных матриц». Объединим ячейки А1-С1 и поместим в них надпись Пример 3.2 а). Выделим все границы ячеек А2—ВЗ и поместим туда элементы матрицы из условия примера 3.2а. В выделенную ячейку С2 поместим встроенную функцию МОПРЕД (А2:ВЗ) и вычислим ее значение. Поскольку определитель равен -14, т. е. не равен нулю, а квадратная матрица имеет второй порядок, то обратная матрица существует, и ее можно найти, используя два пересчета.

Для выполнения первого пересчета в первой строке матрицы выделим первый слева ненулевой элемент. Он находится в ячейке А2. Выделим ее желтым цветом. Это разрешающий элемент. Матрицу, получающуюся после первого пересчета, поместим в выделенные ячейки А5—Вб В ячейку А5 вставляем формулу =1/А2; в ячейку А6 — =В2/А2; в ячейку В5 — =-АЗ/А2; в ячейку Вб — =ВЗ-АЗ*В2/А2. В ячейках А5—Вб получаем матрицу после первого пересчета.

Проведем второй пересчет. Во второй строке полученной матрицы в качестве разрешающего выбираем элемент, стоящий в ячейке Вб. Выделим его желтым цветом. Элемент в ячейке В5 в качестве разрешающего выбрать нельзя, ибо он находится в столбце, в котором находился разрешающий элемент на предыдущем шаге. В ячейку А8 вставляем формулу =А5-А6*В5/В6; в ячейку А9 — =А6/В6; в ячейку В8 — =-В5/В6; в ячейку В9 — =1/Вб. В ячейках А8—В9 получаем матрицу после второго пересчета. Она и является искомой обратной матрицей.

В выделенных ячейках All—В12 вычислим обратную матрицу с помощью функции МОБР (А2:ВЗ).

Замечание. Функция МОБР должна быть введена как функция массива. Для этого сначала необходимо выделить диапазон ячеек, в которых должен быть записан результат, затем ввести функцию МОБР. Далее следует выделить ячейки, в которых находится прямая матрица, а потом нажать комбинацию клавиш Ctrl + Shit + Enter последовательно, удерживая предыдущую. Для удобства представления результатов вычислений можно использовать формат ячеек «Дробный» -* «Дробями до трех цифр». Если вычисления проведены правильно, то матрицы в ячейках А8—В9 и All—В12 должны совпасть (рис. 3.3).

б) Объединим ячейки El—Н1 и поместим в них надпись Пример 3.2 б). Выделим все границы ячеек Е2—G4 и поместим туда элементы матрицы из условия примера 3.2, б. В выделенную ячейку С2 поместим встроенную функцию МОПРЕД (Е2:С4) и вычислим ее значение. Поскольку определитель равен -14, т. е. не равен нулю, а квадратная матрица имеет третий порядок, то обратная матрица существует, и ее можно найти, используя три пересчета.

Для выполнения первого пересчета в первой строке матрицы выделим первый слева ненулевой элемент. Он находится в ячейке Е2. Выделим ее желтым цветом. Это разрешающий элемент. Матрицу, получающуюся после первого пересчета, поместим в выделенные ячейки Е6—G8. В ячейку Е6 вставляем формулу =1/Е2; в ячейку F6 — -F2/E2; в ячейку G6 — =G2/E2; в ячейку Е7 —.

Рис. 3.3. Нахождение обратных матриц методом Жордана — Гаусса.

=-ЕЗ/Е2|; в ячейку F7 — |=F3-E3*F2/E2[; в ячейку G7 — |=G3-E3*G2/E2[;

в ячейку Е8 — =-Е4/Е2; в ячейку F8 — формулу =F4-E4*F2/E2; в ячейку G8 — формулу =G4-E4*G2/E2. В ячейках Еб—G8 получаем матрицу после первого пересчета.

Выполним теперь второй пересчет. В качестве разрешающего выберем элемент F7. Матрицу, получающуюся после первого пересчета, поместим в выделенные ячейки ЕЮ—G12. В ячейку ЕЮ вставляем формулу =E6-E7*F6/F7; в ячейку F10 — формулу =-F6/F7; в ячейку G10 — =G6-F6*G7/F7; в ячейку Е11 — =E7/F7; в ячейку Fll — |=1/F7|; в ячейку Gil — |=G7/F7|; в ячейку Е12 — |=E8-E7*F8/F7]; в ячейку F12 — =-F8/F7; в ячейку G12 — =G8-F8*G7/F7. В ячейках ЕЮ—G12 получаем матрицу после второго пересчета.

Выполним третий пересчет. В качестве разрешающего выберем элемент G12. Матрицу, получающуюся после первого пересчета, поместим в выделенные ячейки Е14—G16. В ячейку Е14 вставляем формулу |=E10-E12*G10/G12|; в ячейку F14 — |=F10-F12*G10/G12[; в ячейку G14 — |==-G10/G12|; в ячейку Е15 — |=E11-E12*G11/G12[; в ячейку F15 — [ =F11-F12*G11/G12|; в ячейку G15 — |=-G11/G12|; в ячейку Е16 — =E12/G12; в ячейку F16 — =F12/G12; в ячейку G16 — =1/G12. В ячейках Е14—G16 получаем матрицу после третьего пересчета. В выделенных ячейках Е18—G20 вычислим обратную матрицу с помощью функции MOBP (E2:G4). Если вычисления проведены правильно, то матрицы в ячейках Е14—G16 и Е18—G20 должны совпасть (рис. 3.3).