Уточнение корня методом хорд и касательных

Хотя метод десятичного деления является универсальным методом численного решения различных типов уравнений, но применение этого метода требует большого объема весьма рутинных вычислений. Имеются менее универсальные методы, но для получения корня уравнения с той же степенью точности они требуют намного меньший объем вычислений. Одним из таких методов является комбинированный метод хорд и касательных.

Метод хорд. Пусть некоторый корень ?, уравнения Дх) = 0 отделен на отрезке [а; Ъ]. Пусть функция Дх) непрерывна, монотонна, имеет выпуклость одного знака (либо выпукла вверх, либо выпукла вниз) и принимает на концах значения разных знаков. График функцииу =Дх) проходит через точки А (а; Да)) и В (Ь;ДЬ)) (рис. 2.10).

Искомый корень есть абсцисса? точки пересечения графика с осью Ох. Эту точку в общем случае найти трудно, вместо нее будем искать близкую к ней точку пересечения хорды АВ с осью Ох (рис. 2.11). Обозначим абсциссу этой точки через ?, j и примем ее за приближенное значение корня данного уравнения. Рассматривая подобные треугольники ААА’А и ААВВ' (рис. 2.11), придем к пропорции.

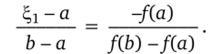
Из этой пропорции найдем.

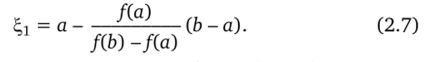
Формула (2.7) называется формулой метода хорд.

Значение ^ может оказаться недостаточно точным. Тогда ту же формулу применяют к отрезку [^; Ь], получают значение ₂

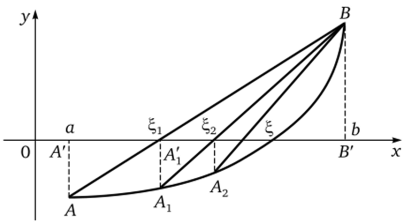
Рис. 2.7 7. К методу хорд.

и т.д. Продолжая этот процесс, придем к приближенному значению корня требуемой точности.

В формуле (2.7) а и b можно поменять местами — тогда получим формулу.

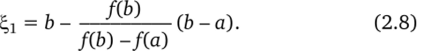
Метод касательных. При тех же исходных условиях корень о уравнения/(х) = 0, отделенного на отрезке [а; Ъ], можно приблизить абсциссами ^и т.д. точек пересечения касательных к кривой с осью Ох (рис. 2.12).

Получим формулу для метода касательных. Так как тангенс утла наклона касательной к кривой в точке А с положительным направлением оси Ох равен /'(а), то из соответствующего прямоугольного треугольника ААА’А находим.

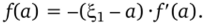
Отсюда.

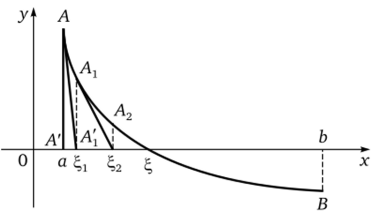
Рис. 2.12. К методу касательных.

Если есть необходимость провести касательную в точке В, то вместо а в формуле (2.9) нужно написать Ь:

Формулы (2.9) и (2.10) есть формулы метода касательных. Если значение оказывается недостаточно точным, то ту же формулу применяют к отрезку [^; Ь], получают значение i;₂ и т. д. Продолжая этот процесс, придем к приближенному значению корня требуемой точности.

Комбинация метода хорд и метода касательных. Итак, приближенное значение корня ?, можно найти, применяя либо метод хорд, либо метод касательных, однако использование комбинации этих методов позволяет очень быстро получить хорошее приближение корня ?, и легко оценить его погрешность. Рассмотрим этот метод.

Вычислим первое приближение по методу хорд, примененному к отрезку [а; Ь], и пусть, для определенности, функция такова, что это приближение меньше истинного значения корня: & <

Поскольку по условию применимости метода функция монотонна, то выполняется неравенство а < Тогда первое приближение корня по методу касательных вычисляется с использованием значения Ъ (формула (2.10) и будет больше истинного значения корня: С другой стороны {,'{ < Ь.

Применяя описанную выше комбинацию метода хорд и касательных к отрезку [%i; ?" ], получаем вторые приближения и %2> для которых справедливы неравенства.

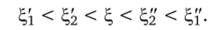
Последовательно продолжая эту процедуру, получаем две последовательности: возрастающую < ?$ < … < ^ ?? > … > ?,% ^> •••> между которыми находится корень уравнения.

Пользуясь этим приемом, обычно довольно быстро можно получить хорошее приближение корня, причем неравенство (2.11) позволяет очень просто оценить погрешность. Так, абсолютная погрешность каждого из приближенных значений Ц и ?,? не превышает.

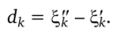
Если же взять приближенное значение корня.

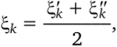
то погрешность не превысит d_k/2.

Если первое приближение по методу хорд, примененному к отрезку [а; Ь], будет больше истинного значения корня: ^ то метод касательных применяется с использованием значения а (см. формулу (2.9)).

Последовательность, полученная по методу хорд, будет убывающей:

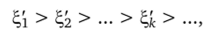
а по методу касательных — возрастающей:

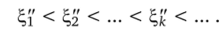
В этом случае неравенство (2.11) записывается в виде.

Абсолютная погрешность каждого из приближенных значений и 2Ц не превышает.

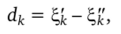
а для приближенного значения корня.

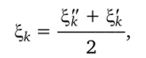
погрешность не превысит d_k/2.

Четыре типа функций. Возможны четыре типа функций, удовлетворяющих исходным условиям: функция Дх) непрерывна, монотонна, имеет выпуклость одного знака (либо выпукла вверх, либо выпукла вниз) и принимает на концах значения разных знаков. Графики этих функций приведены на рис. 2.13.

Первый тип функций характеризуется тем, что функция на отрезке [а; b] возрастает и выпукла вниз.

Пусть во всех точках промежутка (а; Ь) функция Дх) имеет первую и вторую производную. Это означает, что во всех точках промежутка (а; Ь) выполняются следующие неравенства: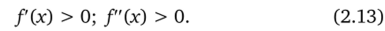

Рис. 2.13. Четыре типа функций.

Если во всех точках промежутка (а; b) выполняются неравенства (2.13), это означает, что функция на отрезке [а; b] возрастает и выпукла вниз, т. е. это функция первого типа. В этом случае для вычисления приближений корня по методу хорд используется формула (2.7), а по методу касательных — формула (2.10). В данном случае выполняется неравенство (2.11).

Второй тип функций характеризуется тем, что функция на отрезке [а; Ь] убывает и выпукла вверх.

Если во всех точках промежутка (а; Ь) функция Дх) имеет первую и вторую производную, то во всех точках промежутка (а; b) выполняются следующие неравенства:

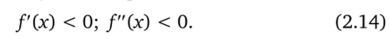
Если во всех точках промежутка (а; Ь) выполнены неравенства (2.14), это означает, что функция на отрезке [а; b] убывает и выпукла вверх, т. е. это функция второго типа. В этом случае, как и для функций первого типа, для вычисления приближений корня по методу хорд используется формула (2.7), а по методу касательных — формула (2.10). В данном случае выполняется неравенство (2.11).

Третий тип функций характеризуется тем, что функция на отрезке [а; Ь] возрастает и выпукла вверх.

Если во всех точках промежутка (а; Ъ) функция Дх) имеет первую и вторую производную, то во всех точках промежутка (а; Ь) выполняются следующие неравенства:

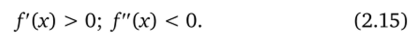
Если во всех точках промежутка (а; Ь) выполняются неравенства (2.15), это означает, что функция на отрезке [а; b] возрастает и выпукла вверх, т. е. это функция третьего типа. В этом случае для вычисления приближений корня по методу хорд используется формула (2.8), а по методу касательных — формула.

(2.9). В данном случае выполняется неравенство (2.12). Четвертый тип функций характеризуется тем, что функция на отрезке [а; b] убывает и выпукла вниз.

Если во всех точках промежутка (а; b) функция Дх) имеет первую и вторую производную, то во всех точках промежутка (а; Ь) выполняются следующие неравенства:

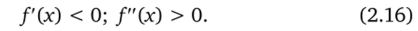
Если во всех точках промежутка (а; b) выполняются неравенства (2.16), это означает, что функция на отрезке [а; Ь] убывает и выпукла вниз, т. е. это функция четвертого типа. В этом случае для вычисления приближений корня по методу хорд используется формула (2.8), а по методу касательных — формула.

(2.9). В данном случае выполняется неравенство (2.12).

Пример 2.3.

Найдите корень уравнения х³ — бх² + 20 = 0 из отрезка [2; 3] с точностью до 10~⁷ методом хорд и касательных.

Решение

Найдем тип функции Дх) = х³ — бх² + 20 на отрезке [2; 3]. На этом отрезке.

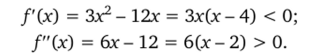
Следовательно, имеет место четвертый тип функции. В этом случае.

На ПК откроем книгу «Решение уравнений» Microsoft Excel и переименуем ее второй лист так: «Метод хорд и касательных». В ячейку А1 запишем а=, в ячейку С1 — Ь=, в ячейку Е1 — f (a)=, в ячейку G1 — f (b)=. Поскольку для четвертого типа функции в формуле (2.9) метода касательной используется значение /'(а), в ячейку II записываем f'(a)=. В ячейку В1 вставим значение левого конца отрезка (значение 2), в ячейку D1 вставим значение правого конца отрезка (значение 3). В ячейку F1 вставим формулу, вычисляющую значение/(2), а в ячейку Н1 — формулу, вычисляющую значение ДЗ). В четвертом типе функции в формуле (2.9) метода касательной используется значение/'(а), в силу этого в ячейку Л мы должны вставить формулу, вычисляющую значение/'(2) (рис. 2.14).

Рис 2.14. Вычисление корня уравнения х³ — бх² + 20 = О на отрезке [2; 3] методом хорд и касательных В силу того что для четвертого типа функции для приближений корня выполняется неравенство ?? < в ячейку А2 запишем? Г'=, в ячейку С2 — ?Г=, в ячейку Е2 — f (Jjl")=, в ячейку G2 —f (?l')=, в ячейку 12 — f'(?l")=. Теперь в ячейку В2 вставим формулу (2.9) из метода касательных:

>

в ячейку D2 вставим формулу (2.8) из метода хорд:

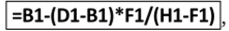
в ячейку F2 вставим скопированную ячейку F1, в ячейку Н2 вставим скопированную ячейку Н1, а в ячейку J2 — скопированную ячейку Л.

Мы сделали первую итерацию метода. В ячейках В2 и D2 вычисляются приближенные значения корня и В ячейках D2, F2 и J2 вычисляются значения/(??),/(?!) и/'(^) соответственно (рис. 2.13).

Поскольку значения = 2,333 333 333 и = 2,363 636 364 имеют всего один общий десятичный знак после запятой, то проводим вторую итерацию метода. Для этого скопируем ячейки диапазона А2—J2 и вставим в ячейки диапазона АЗ—J3. После этого исправим в ячейках АЗ, СЗ, ЕЗ, G3 и 13 индексы 1 на индексы 2. В ячейках ВЗ и D3 вычисляются приближенные значения корня ?2 ^и %2- Результаты второй итерации таковы: = 2,336 507 937 и & = 2,336 516 455. Полученные значения имеют только четыре общих десятичных знака, т. е. требуемая точность пока не достигнута.

Аналогично второй итерации проведем третью итерацию. Результаты третьей итерации таковы: ?2 = 2,336 508 804 и ^ = = 2,336 508 804. Полученные значения имеют девять общих десятичных знаков, т. е. требуемая точность получена. Округляя полученные значения до семи знаков, получим значение корня с точностью до 1СГ⁷: ~ 2,3 365 088. Все выписанные знаки корня верные.

Предлагаем читателю найти два других значения корня уравнения х³ — бх² + 20 = 0 с точностью до 10~⁷ методом хорд и касательных. (Ответ: ?, ~ 2,3 365 088).