Проверка статистических гипотез

Теперь, когда имеются сведения о законе распределения признаков, можно приступить к описанию исследуемой выборки. Но поскольку исследователя в большей степени интересует не выборка, а генеральная совокупность (популяция), из которой эта выборка извлечена, то начальный процесс статистического анализа выборочных данных представляет собой проверку тех или иных статистических гипотез. В зависимости от решаемых задач это могут быть гипотезы о различии средних выборки и популяции, о равенстве средних значений зависимых или независимых групп, о равенстве дисперсий и другие. После выбора статистического критерия производится расчет его значения, то есть достигнутый уровень значимости р, и сравнение с критическим уровнем (0,05; 0,01 или 0,001 по выбору исследователя).

На основании результата сравнения гипотеза отвергается или принимается.

Уровень значимости р — это рассчитанная в ходе статистического теста вероятность ошибочно отвергнуть гипотезу. Например, о равенстве средних значений или о соответствии закона распределения нормальному, когда в действительности средние значения разных групп равны или закон распределения соответствует нормальному. Поскольку выбор критического уровня статистической значимости в некоторой степени является произвольным, то рекомендуется указывать его точное значение до трех десятичных знаков, а не указывать только интервалы, в которых результаты являются статистически незначимыми (р > 0,05) или значимыми (р < 0,05). Например, для результатов проверки закона распределения на нормальность для параметра объем услуг по критерию Лиллиефорса получили статистически незначимый результат (р < 0,1), а по W-критерию ШапироУилка статистически значимый результат (р = 0,039). Поэтому по W-критерию распределение параметра объем услуг можно считать близким к нормальному.

Для обнаружения различия между средними показателями различных выборок широко используется t-критерий, если признаки распределены по нормальному закону. Применим этот критерий для проверки гипотезы о равенстве средних значений признака объем услуг для независимых групп: санаториев и пансионатов. Для этого необходимо выполнить следующие команды: «Статистика / Основная статистика и таблицы / Описательная статистика / t-test, independent, by groups». В появившемся диалоговом окне следует выбрать в качестве зависимого признака объем услуг и группирующего признака тип предприятия. При этом необходимо иметь в виду, что данный t-критерий применим только при одновременном выполнении двух условий: значения признаков в каждой группе должны иметь нормальный закон распределения и дисперсии признаков в сравниваемых группах равны. Условие нормальности для данного признака выполняется (рис. 6.11−6.13), а условие равенство дисперсий можно проверить по критерию Левена, для чего следует активизировать опцию «Тест Левена» в том же диалоговом окне. Щелкнув клавишей мыши по кнопке «Итог: Т-тесты», получаем окно результатов сравнения двух независимых групп (рис. 6.14).

Рис. 6.14. Результаты проверки гипотезы о равенстве средних значений признака объем услуг для независимых групп по t-критерию.

Значение уровня значимости р > 0,05 для критерия Левена означает равенство дисперсий, а значение уровня р = 0,173 для t-критерия свидетельствует о выполнении нулевой гипотезы о равенстве средних значений признака объем услуг в двух независимых группах: пансионаты и санатории.

Если выполнить анализ для признака количество работающих, то закон его распределения отличается от нормального (р > 0,2), и поэтому для проверки гипотезы о равенстве средних значений следует использовать непараметрические методы, среди которых наиболее популярным является U-критерий Манна-Уитни. Этот критерий применим для количественных и порядковых признаков. Для его применения следует выполнить команды: «Статистика / Основная статистика и таблицы / Непараметрические методы / Comparing two independent groups». В появившемся диалоговом окне «Сравнение двух групп» следует выбрать зависимые переменные (объем услуг и количество работников), группирующий признак тип предприятия и щелкнуть по кнопке «U-тест Манна-Уитни» (рис. 6.15).

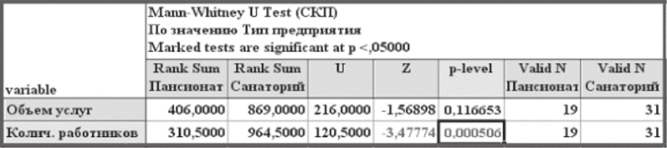
Рис. 6.15. Результаты проверки гипотезы о равенстве средних значений признака количество работников для независимых групп по U-критерию Манна-Уитни.

Для признака количество работников по U-критерию МаннаУитни принимается гипотеза о существовании различий групп с уровнем статистической значимости р = 0,0005, в то время как для признака объем услуг нулевая гипотеза об отсутствии различий групп не отклоняется (р = 0,117).

В подобных ситуациях могут быть применены также другие непараметрические методы: критерий Вальда-Вольфовица и двувыборочный критерий Колмогорова-Смирнова. В принципе непараметрические методы могут применяться и для признаков с нормальным законом распределения, но в этом случае они менее чувствительны, чем параметрические методы.

В настоящее время для представления результатов исследования наряду с проверкой статистических гипотез широко используется доверительный интервал. В ответственных случаях рекомендуется применять оба этих подхода при анализе статистических данных.

Доверительный интервал — это интервал значений признака, рассчитанный для какого-либо параметра по выборке (например, среднее значение признака, коэффициент корреляции), с определенной вероятностью (обычно 95%), включающий истинное значение этого параметра во всей генеральной совокупности^[1]. Другимн словами, выбор доверительного коэффициента равным 95% означает, что в 95 выборках из 100, сделанных таким же способом из генеральной совокупности объектов исследования, оценка параметра признака будет находиться в рассчитанном доверительном интервале.

Применение доверительного интервала не ограничивается видом закона распределения. Для законов, отличающихся от нормального, доверительный интервал будет несимметричным относительно среднего значения. Его ширина определяется объемом выборки и величиной дисперсии рассматриваемого признака. При увеличении доверительного коэффициента, например, с 95 до 99%, то есть при увеличении степени уверенности, ширина доверительного интервала расширяется.

Для определения величины доверительного интервала следует выполнить следующие команды: «Статистика/Основная статистика и таблицы/ Описательная статистика». В появившемся окне «Описательная статистика» необходимо выбрать признаки, для которых необходимо рассчитать доверительный интервал, активизировать опцию «Границы доверительного интервала», установить величину «Доверительного коэффициента» и щелкнуть по кнопке «Итог: описательная статистика» (рис. 6.16). Для признака объем услуг среднее значение находится в интервале (46 438; 71 270). Если доверительный коэффициент увеличить до 99%, то интервал расширится до значений (42 296; 75 412).

Рис. 6.16. Результаты расчета доверительного интервала.

Доверительный интервал можно также использовать для сравнения групп, используя, например, диаграмму Whisker (рис. 6.17). Для этого следует выполнить команды: «Статистика/Описательная статистика/t-test, independent, by groups».

Установить необходимые зависимые и группирующие параметры в появившемся диалоговом окне и щелкнуть по кнопке «объемное и точечное вычерчивание». В результате получаем графическое изображение гипотезы о существовании различий групп для признака количество работников по U-критерию Манна-Уитни с помощью доверительного интервала (±1,96SD).

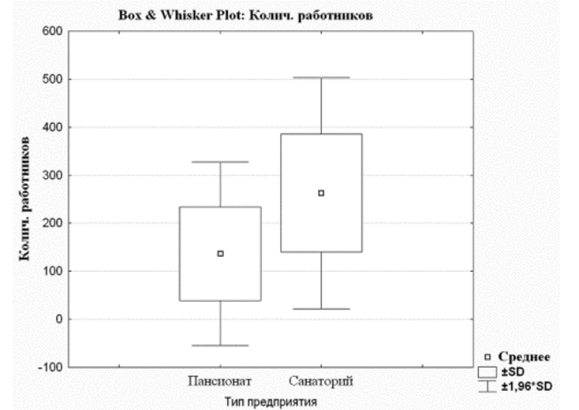
Рис. 6.17. Сравнение двух групп по признаку количество работников с помощью доверительного интервала на базе диаграммы Whisker.

• [1] Реброва А. Ю. Статистический анализ медицинских данных. Применение пакета прикладных программStatistica. — М.: Медиа Сфера. 2003.