Операции над множествами

Система всех подмножеств множества X называется булеаном множества X, обозначается 2^х. Включение множеств с обладает свойствами:

• • рефлексивности — X с X;
• • транзитивности — если ХсУ, У с Z, то X с Z;
• • антисимметричности — если Хс У, У с X, то X = У.

Равенство множеств обладает свойствами рефлексивности и транзитивности. Включение с обладает свойством транзитивности.

Обычно подмножества X, У, … берутся из множества /У, называемого универсальным множеством, или универсумом. Определим для них теоретико-множественные операции:

• 1) объединение — X и У = {х: х е X или хе У), отсюда max{ | Y, |х|} < < |Хи У| < |У| + IX|;
• 2) пересечение — Хп У={х:хе ХихеУ}, отсюда 0 < | X п У | < min{ | У|, |Х|}.

Множества, не имеющие общих элементов, называют непересекающимися, записывают X п У = 0.

Множество R множеств замкнуто относительно операции •, если из включений Х> Y е R следует включение X • У е R. Кольцом множеств называется система множеств, замкнутая относительно операций объединения и пересечения. Булеан универсума образует кольцо. Множество элементов n-множества при п > 1 не образует кольца;

• 3) разность — ХУ={гхеХ ихб У}, отсюда 0 < | X У | < I Х|. Если У с X, то множество X У называют дополнением множества У до X;
• 4) дополнение множества X (обозначается X) — X = UX, отсюда IX | =

= и — |х|;

• 5) симметрическая разность — ХДУ = (X и У) (X п У);
• 6) декартово произведение — X х У = {(х, у) х е X, у е У}, отсюда | X х У| =

= 1х| • |У|.

Декартовым произведением множеств Х_{, Х_т называется множество наборов {(х_{, х_т)}, где х_} е X_jf i = 1 , т, т е N. Несложно доказать (математическая индукция), что.

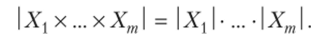
Декартово произведение т одинаковых сомножителей X х … х X обозначается Х^т и называется т-й декартовой степенью множества X. Элемент (Ху, х_т) множества Х^т называют словом длины т в алфавите X или последовательностью длины т над X (набором размера т элементов X). Число различных слов длины т в алфавите порядка п равно п^т.

Пример 1.4.

Для Х = {1,2,3, 4>, Y = {4, 5} верно Xu У={ 1,2, 3, 4, 5}, Хп У={4}, УХ={5}, XY={ 1,2,3}, Хх У= {((1,4), (1,5), (2,4), (2,5), (3,4), (3,5), (4,4), (4,5)}, Y2 = {(4,4), (4, 5), (5, 4), (5, 5″, 2>'= {0, {4>, {5}, {4, 5}}. >

Утверждение 1.1. Если X есть «-множество, то 12^х | = 2^п.

Ч Любому подмножеству Y множества X = {х_и х_п}) взаимно однозначно соответствует вектор a_Y= (a_l5а_п) из нулей и единиц, где a, = 1 Xj G У, i = 1,". Тогда 2^Х = |{0, 1}"| =2″. ?

Для операций над подмножествами X, У, Z универсума U верны следующие свойства:

• 1) идемпотентность — X и X = I, X п X = X;
• 2) коммутативность — ХиУ=УиХ; ХпУ=УпХ;
• 3) ассоциативность — (Xu У) u Z = X и (У u Z); (X n Y) п Z = X п п (Уп Z);
• 4) дистрибутивность — Xп (Yu Z) = (Xп У) u (X n Z); Xи (Уn Z) = = (X и У) n (X и Z);
• 5) поглощение — (Хп У) иХ = Х;(Хи У) п X = X;
• 6) свойства нуля — Хи0 = Х;Хп0 = 0;
• 7) свойства единицы — Xu U =U X п [/ = X;
• 8) свойства дополнения — XuX = t/;XnX = 0;
• 9) инволютивность — X = X; ___
• 10) законы де Моргана — ХпУ = ХиУ;ХиУ = ХпУ.

Для наглядного представления операций над множествами используются изображения множеств точек плоских фигур (кругов или прямоугольников), размещенных внутри другой фигуры, рассматриваемой как универсум.

На рис. 1.1 операции объединения и пересечения множеств представлены графически с помощью диаграмм Венна. Результат операции изображен закрашенной областью.

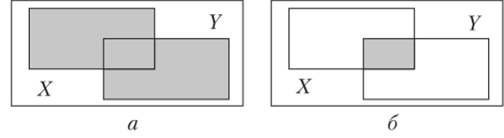
Рис. 1.1. Диаграммы Венна объединения (а) и пересечения (б) множеств.