Тензорное произведение матриц, спектральное представление

Определим кронекерово (тензорное) произведение квадратных матриц над полем Р (обозначается ®). Пусть А = (ау), В = (Ь^), где А е М_Р(г), В е М_Р(п). Тогда матрица А ® В = (а^В) е М_Р(т), она получена заменой каждого элемента аматрицы А на матрицу a_tJB. Тензорное умножение матриц не коммутативно. Например, Е ® А, А ® Е, где Е, А — матрицы над полем Q:

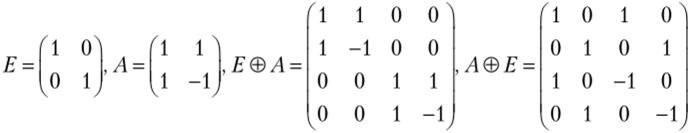
Справедливы следующие свойства:

• 1) ассоциативность: А ® (В ® С) = (А ® В) ® С;
• 2) дистрибутивность: (А + В)®С-А®С + В®С, А®(В + С)-А®В + + А®С-,
• 3) для А, С е М_Р(п) и В, D е М_Р(г) выполнено: (Л ® В)(С ® D) = АС ® ®BD;
• 4) из свойства 3) имеем: матрица А ® В обратима обратимы матрицы А и В, при этом (Л ® В)~¹ = Л^-1 ® /Н.

Тензорная степень матрицы определена индуктивно: Лt¹1 = Л, Л1″ 1 = Л ® (r) Л!"^-11, п = 2, 3,…, отсюда (ЛВ)Н = Л1″ 1В1″ 1.

Для линейной б.ф. (а, х) = а_хх_х © … © а_Г1х_п, где а = (а_х, …, а_п) е V_n, определим функцию (-1)(«•*>: V, —> (-1, 1}, где (-1)(«•-') = 1, если (а, х) = = 0, и (-1)(«.-*) = -1, если (а, х) = 1. Всего имеется 2» функций вида (_1)(я,.г) Например, векторам (0,…, 0) и (1,…, 1) соответствуют функции 1 и (-l)^ri®» ® V Все эти функции образуют ортогональную систему.

Лемма 6Л. Для любых векторов a, b е V_n.

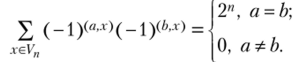
Ч Исходная сумма равна ^ (-1)(«**? -^г'). При а = b каждое слагаемое.

x

полученной суммы равно 1, а при а b линейная функция (а, х) принимает значения 0 и 1 по 2″ ^-1 раз. ?

Теорема 6.6 (о разложении в ряд Фурье). Для любой б.ф. имеется единственное разложение вида.

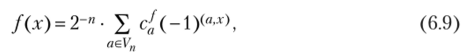
где х = (ж₁₍…, х") е V_n и коэффициенты с{_: суть целые числа, определяемыми равенствами.

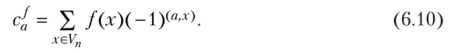
Л Подставляя в равенства (6.9) вместо коэффициентов с{ их выражения (6.10), имеем.

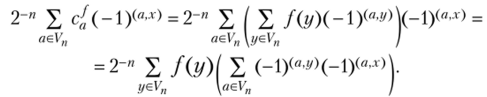
По лемме 6.1 сумма внутри скобок равна 0 при х * у и равна 2″ при х = у. Отсюда.

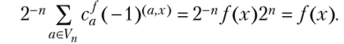
Если коэффициенты с{ определены неоднозначно, то имеется другое разложение /(ж) вида (6.9): f (x) = 2 ^п? Д/(-1)^(я'-^г). Вычитая одно разложи жение из другого, получим.

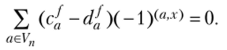
Умножая равенства на (-1)(*.*), где b е V_n, и суммируя затем по х е V", получим.

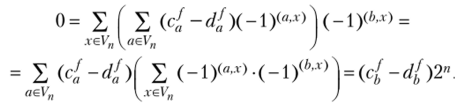
Отсюда с[ = d[, где b — любой вектор из V_n. ?

Вектор коэффициентов C (f) = (с/), а е V_n, называют спектром Фурье, его координаты — коэффициентами Фурье б.ф./(ж). Преобразование вектора таблицы б.ф. /(ж) в спектр Фурье называют преобразованием Фурье

б.ф. f (x). Оно выполняется с помощью умножения на матрицу Адамара — Сильвестра #₂", которая есть п-я тензорная степень матрицы порядка 2:

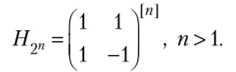
Наряду с б.ф. /(х) рассматривают ее действительнозначный аналог f_(!(x) = (-1)/(*). Отображение таблицы функции //х) с помощью матрицы Я₂" называют преобразованием Уолша — Адамара б.ф./(.г). Получаемый вектор коэффициентов Z (J) = (z{), а е V_n, называют спектром Уолша — Адамара, его координаты — коэффициентами Уолша — Адамара б.ф. /(х):

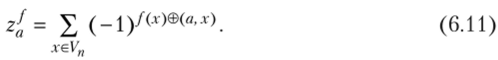
Спектры Фурье и Уолша — Адамара всякой б.ф. взаимосвязаны.

Теорема 6.7. Для всякой б.ф./(х) и любого а е V_n выполнено:

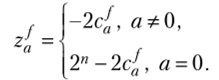
4 При а = 0 из (6.10) и (6.11) соответственно имеем с/ = ||/||, Zq = 2″ - 2||/||. Обозначим для б.ф. /(х), g'(x) через А_е 8(/, g), где е, 8 е {0,1}, число векторов х из V_n, для которых /(х) = е и g (x) = б. Тогда из (6.10) и (6.11) при а Ф 0 получаем с{= N_uo(f,(a, х" - А,(/,(«, х»,.

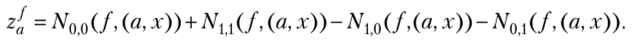
Отсюда следует утверждение теоремы, если учесть, что Л'₀₀(/, (а, х)) = = 2″ -> - N, ₀(/, (а, х", ,(/, (а, х)) = I 1/1 I — Aj ₀(/, (а, х)), А_{0 X}(J, (а, х)) =

⁼ 2″ ^-1 —1|/1 + А₁₀(/, (а, х)). ?

Из (6.10) следует, что с[ - ||/||, т. е. 0 < с[ < 2″, а остальные коэффициенты Фурье б.ф./(х) — это целые числа из сегмента [-2^л-1, 2″^-1]. Не всякий набор целых чисел с данными ограничениями является спектром Фурье некоторой б.ф. Коэффициенты Фурье (и коэффициенты Уолша — Адамара) любой б.ф. связаны некоторыми соотношениями. Например, из (6.9) следует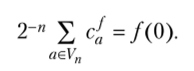

Обозначим через E/_v (через Еf) строку-таблицу значений функции.

^A/._v(«) (Ау (м)).

Теорема 6.8 (о взаимной корреляции)^[1]. Для любых функций f, i е Р>(п):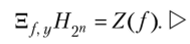

Следствие. Aj (u)H_2n = ((г/)², а е V_n). О Коэффициенты Уолша — Адамара любой б.ф. связаны соотношениями ортогональности при Ъ е V_n сумма? ^zl^zl®b Р^авна 2^2/?, если h = О, и равна нулю, если b Ф 0. Отсюда при b = 0 имеем равенство Парсеваля: X (²а)² «2²» .

Равенство Парсеваля может быть использовано для различения спектров Уолша — Адамара б.ф. от наборов целых чисел, таковыми не являющихся.

• [1] Логачёв О. А., Сальников А. А., Ященко В. В. Булевы функции в теории кодированияи криптологии. М.: МЦНМО, 2004.