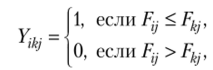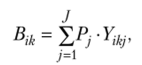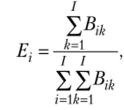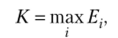Принятие решений с использованием принципа Байеса и оценок альтернатив, заданных в порядковой шкале

Данный метод предназначен для согласования экспертных оценок альтернатив (выигрышей, возникающих в случае выбора той или иной альтернативы) в различных проблемных ситуациях с использованием принципа Байеса. При этом выигрыши задаются в порядковой (ранговой) шкале. Обозначение метода в ЭСППР — BAJPOR.

В качестве возможных вариантов решения рассматривается набор из I альтернатив X = (А, Х₂,…, X_t,…, X,), i = 1, 2,…, I.

Решение принимается при наличии J проблемных ситуаций S = (.S', S₂,.

…, S,…, S,), j =1,2…J. Каждая из проблемных ситуаций появляется с веро;

J

ятностью Pj, j =1,2, YjPj = 1- 7=1.

Для каждой альтернативы в каждой проблемной ситуации известен выигрыш, заданный в порядковой шкале (чем меньше ранг выигрыша — тем предпочтительнее альтернатива). В результате формируется матрица выигрышей размерности / х /, где / — количество возможных вариантов решения (альтернатив),/ — количество проблемных ситуаций. Элемент матрицы выигрышей Fjj представляет собой выигрыш, получаемый в результате выбора варианта решения X, — в j-й проблемной ситуации, заданный в порядковой шкале (г = 1, 2,…, I;j = 1, 2,…,/).

Алгоритм решения задачи предусматривает выполнение следующих шагов.

Шаг 1. Формирование матриц парных сравнений. На данном шаге формируются матрицы парных сравнений, в которых попарно сопоставляются все альтернативы в каждой ситуации. Элементы матриц парных сравнений Y_jkj (г, k = 1,2, …, /; j = 1,2, для всех возможных пар рассматриваемых альтернатив определяются для всех проблемных ситуаций следующим образом:

где — элемент матрицы выигрышей, заданный в порядковой шкале для i-й альтернативы в/-й проблемной ситуации (г = 1, 2,…, /; j = 1, 2…/);

F_kj — элемент матрицы выигрышей, заданный в порядковой шкале для к-й альтернативы в j-й проблемной ситуации (к = 1, 2,…, F, j - 1, 2,…,./).

Шаг 2. Формирование обобщенной матрицы. Элементы обобщенной матрицы B_jk (г, к = 1, 2, …, I) для всех возможных пар рассматриваемых альтернатив определяются следующим образом:

где Y_ikj — элемент матрицы парных сравнений для г-й и к-и альтернатив в j-й проблемной ситуации (г, k = 1, 2,/;у =1,2, …,/);

Р; — вероятность появления /-й проблемной ситуации (/=1,2, …,/).

Шаг 3. Определение коэффициентов среднего выигрыша альтернатив. На данном шаге для всех рассматриваемых альтернатив определяются коэффициенты среднего выигрыша Е, (г = 1, 2, …, Г) по формуле.

где B_jk — элемент обобщенной матрицы для г-й и /г-й альтернатив (г, /г = 1,.

2,… /).

Шаг 4. Ранжирование альтернатив. На данном шаге альтернативы упорядочиваются по убыванию коэффициентов среднего выигрыша (i= 1,.

2,…, Г). Альтернатива с наибольшим значением коэффициента ^ считается наиболее предпочтительной и получает ранг 1, альтернативе со вторым по величине значением коэффициента E_t присваивается ранг 2 и т. д.

Таким образом, оптимальной считается альтернатива, определяемая критерием Байеса:

где Б, — коэффициент среднего выигрыша г-й альтернативы (г = 1, 2,…, /).