Биомеханика мышцы. 
Разработка и применение компьютерной системы тестирования по биофизике

Мышцы можно представить как сплошную среду, то есть среду, состоящую из большого числа элементов, взаимодействующих между собой без соударений и находящихся в поле внешних сил [6].

• 1 Упругость — свойство тел менять размеры и форму под действием сил и самопроизвольно восстанавливать их при прекращении внешнии.
• 2 Вязкость — внутреннее трение среды.
• 3 Вязкоупругостъ — это свойство материалов твердых тел сочетать упругость и вязкость.
• 4 Деформация — относительное изменение длин:

.

5 Напряжение механическое с — мера внутренних сил, возникающих при деформации материала. Для однородного стержня:

.

В таблица 1 приведены значения Е для различных материалов.

Таблица 1 Значения модуля Юнга для различных материалов.

Эластин — упругий белок позвоночных, находится, в основном, в стенках артерий. Коллаген — волокнистый белок. В мышцах 20% всех белков — коллаген. Находится также в сухожилиях, хрящах, кости.

В случае вязкой среды напряжение определяется скоростью деформации dе / dt:

.

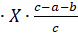
Для вязкоупругой деформации характерна явная зависимость е от процесса нагружения во времени, причем при снятии нагрузки деформация с течением некоторого времени самопроизвольно стремится к нулю.

Пассивные механические свойства вязкоупругой среды можно моделировать сочетанием упругих и вязких элементов.

Вязкость моделируется (изображается) демпфером л, а упругость пружиной Е.

Мышца не является ни чисто упругим, ни чисто вязким элементом. Мышца — вязкоупругий элемент.

Пассивное растяжение. На основании расчетных и экспериментальных данных показано, что наиболее простой моделью, дающей достаточно хорошее приближение к механическим свойствам мышцы, является трехкомпонентная модель Хилла (рисунок 5).

Рисунок 5 Трехкомпонентная модель мышцы (СЭ — сократительный элемент) Для установления характерной зависимости деформации мышцы во времени при приложении к ней мгновенного воздействия упростим модель (рисунок 5). Допустим, что элемент Е2 отсутствует (у2 = 0). Тогда для вязкоупругой среды напряжение, а в системе будет определяться упругой и вязкой составляющими:

.

.

Найдем зависимость E (t), решая дифференциальное уравнение и считая, что в начальный момент времени t = 0 деформация е = 0.

В результате получим:

(1).

где величина называется временем запаздывания.

Скорость нарастания деформации максимальна при t = 0:

.

Отсюда следует, что чем больше величина вязкой компоненты, тем меньше угол наклона кривой е (t).

Деформация е (t) растет с убывающей скоростью и асимптотически приближается к стационарному значению е ст:

.

Таким образом, зависимость (1) достаточно хорошо описывает процесс нарастания деформации е (t), полученный в эксперименте.

В терминах механической модели (рисунок. 5) и модели скользящих нитей (рисунок. 3) параллельный упругий элемент Е1 определяет механические свойства внешних мембран клеток (сарколеммы) и внутренних структур — Т-системы и саркоплазматического ретикулума.

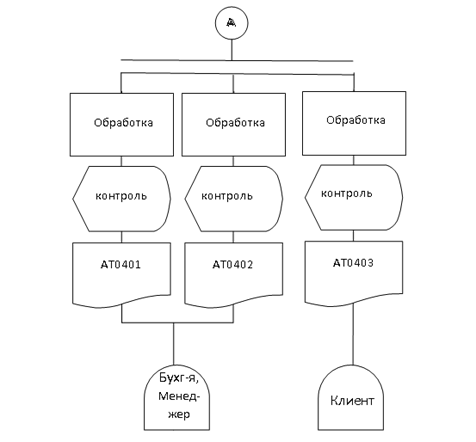
Активное сокращение мышцы. Для исследования характерисуноктик сокращающихся мышц используют два искусственных режима:

• 1 Изометрический режим, при котором длина мышцы I — const, а регистрируется развиваемая сила F (t).
• 2 Изотонический режим, при котором мышца поднимает постоянный груз Р — const, а регистрируется изменение ее длины во времени Al (t).

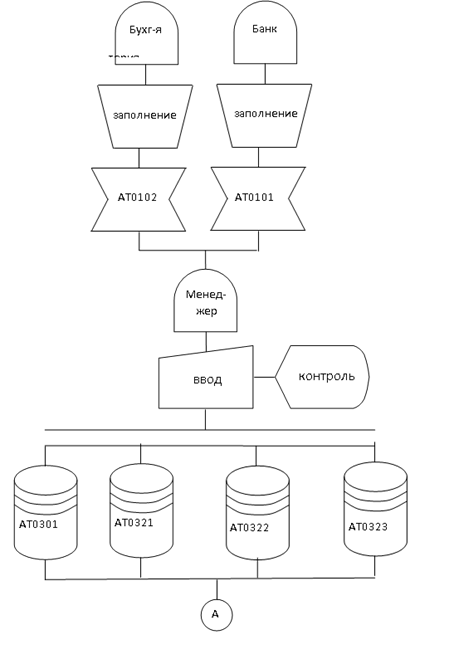
При изометрическом режиме с помощью фиксатора (рисунок. 6, а) предварительно устанавливают длину мышцы I. После установки длины на электроды Э подается электрический стимул и с помощью датчика регистрируется функция F (t).

Рисунок 6 Схемы опытных установок для реализации в эксперименте изометрического (а) и изотонического (б) режимов Вид функции F (t) в изометрическом режиме для двух различных длин представлен на рисунок 7, а.

Рисунок 7 Временная зависимость одиночного сокращения при: а — изометрическом и б — изотоническом режимах сокращения мышцы Максимальная сила Ро, которую может развивать мышца, зависит от ее начальной длины и области перекрытия актиновых и миозиновых нитей, в которой могут замыкаться мостики: при начальной длине саркомера 2,2 мкм в сокращении участвуют все мостики (см. рисунок 4).

Поэтому максимальная сила генерируется тогда, когда мышца предварительно растянута на установке (рисунок. 6, а) так, чтобы длины ее саркомеров были близки к 2,2 мкм. На рисунок 7, а это соответствует начальный длинам двух мышц 1^ и 1 Г. Но так как количество мостиков в мышце ^ больше, чем в l2 (Zt > l2), то сила, генерируемая lt больше.

При изотоническом режиме к незакрепленному концу мышцы подвешивают груз Р (рисунок 6, б). После этого подается стимул и регистрируется изменение длины мышцы во времени: Al (t). Вид этой функции в изотоническом режиме для двух различных нагрузок показан на рисунок. 7, б.

Как следует из рисунок 7, б, чем больше груз Р, тем меньше укорочение мышцы и короче время удержания груза. При некоторой нагрузке Р = Ро мышца совсем перестает поднимать груз; это значение Ро и будет максимальной силой изометрического сокращения для данной мышцы (рисунок. 7, а).

Здесь важно отметить, что при увеличении нагрузки угол наклона восходящей части кривой изотонического сокращения уменьшается (рисунок. 7, б): <�х2 < ах.