Средства композиции. 
Композиция костюма

Пропорции. В математике пропорцией (от лат. proportio) называется равенство между двумя отношениями четырех величин а:Ъ = c:d, в искусстве — пропорции — размерные соотношения элементов формы.

С древнейших времен человечество было занято поиском формулы красоты. Начиная с древнегреческих философов, математиков и художников проводились теоретические исследования для нахождения самых совершенных гармоничных пропорций. Гармония (от греч. harmonia — связь, стройность, соразмерность) — соразмерность частей, слияние различных компонентов объекта в единое органичное целое. В древнегреческой философии гармония рассматривалась как организованность космоса, противостоящая хаосу, в истории эстетики — как существенная характеристика прекрасного.

Известный древнегреческий мыслитель и математик Пифагор Самосский (VI в. до н. э.) изучал свойства целых чисел и пропорций. Он хотел «алгеброй проверить гармонию». Пифагор и его последователи считали число как основу всего существующего, а числовые отношения — источником гармонии космоса. Они утверждали, что треугольник есть первоисточник рождения и сотворения различных видов вещей. Отсюда дошла до наших дней теорема Пифагора с его знаменитым треугольником: прямоугольный треугольник с углами в 30, 60 и 90° и гармоничным соотношением его сторон. Кроме того, Пифагор считал, что квадрат в большей степени, чем любая другая фигура, несет в себе образ «божественной природы». Это была излюбленная им математическая фигура, которая символизировала высокое достоинство, так как прямизна углов передает целостность, а качество сторон способно устоять перед силой. Видимо, те же качества подразумевались и в «Черном квадрате» К. Малевича.

Пропорции можно разделить на две группы: простые (основанные на рациональных числах) и сложные (основанные на иррациональных числах, производных геометрических построений). Простые пропорциональные отношения выражаются простыми числами. К ним относится так называемый египетский треугольник с гармоничным соотношением сторон 3:4:5 (рис. 3.3, а).

Архитектор эпохи Возрождения Л. Б. Альберти в своем сочинении «Десять книг о зодчестве» писал: «Вновь и вновь следует повторить изречение Пифагора: «Нет сомнений, что природа во всем остается себе подобной. Дело обстоит так: существуют числа, благодаря которым гармония звуков пленяет слух, эти же числа преисполняют и глаза и дух чудесным наслаждением». Музыкальная аналогия навела Альберти на мысль о том, что глазу доставляет наслаждение наблюдать пропорции, представляемые в виде отношений целых чисел. Например, числа 1, 3, 5, 7, 9,11… образуют арифметическую прогрессию, а последовательность чисел 1,½, 1/3,¼… —гармоническую последовательность. Он использовал музыкальные пропорции для того, чтобы установить взаимосвязь между тремя измерениями: высотой, длиной и шириной.

Древние греки вывели иррациональное число Фи (ф), которое символизировало пропорции «золотого сечения». Буква ф — первая греческая буква в имени великого скульптора Фидия, который часто использовал пропорции «золотого сечения» в своих скульптурах. Термин «золотое сечение» появился намного позднее. Таким образом, число ф как раз и равнялось отношению отрезков при делении прямой в «крайнем и среднем» положениях: АВ:ВЕ = АЕ: АВ = ф (рис. 3.3, б).

Много замечательных свойств числа ф было описано в трактате итальянского математика XV в. Л. Пачоли, который изложил теорию геометрических пропорций с иллюстрациями Леонардо да Винчи. Он исследовал «золотой прямоугольник», который обладал необычными свойствами. Отрезав от этого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, снова можно получить «золотой прямоугольник» меньших размеров, и так до бесконечности. В этот прямоугольник вписывается логарифмическая спираль, образованная «вращающимися квадратами». В природе по такой спирали строится раковина моллюска Nautilus. Логарифмическая спираль тесно связана с числами Фибоначчи (1, 2, 3, 5, 8, 13, 21, 34…) или квадратами Фибоначчи с резким убыванием сторон по отношению к диагонали (рис. 3.4, а). Эти числа, где каждое последующее число, начиная с третьего, равно сумме двух предыдущих, придумал математик Леонардо из Пизы по прозвищу Фибоначчи в XIII в.

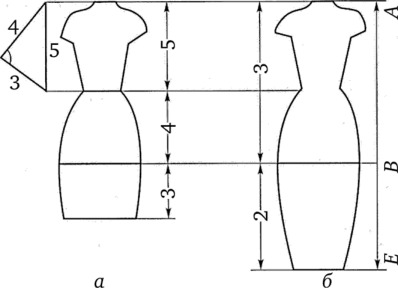
Рис. 3.3. Пропорциональные отношения: а — в египетском треугольнике: б — пропорции «золотого сечения».

Иллюзию постепенного, едва заметного убывания дают динамические прямоугольники и прямоугольники с соотношениями сторон 1 / V2,1 / л/3,1 / [s, 1/л/8… (рис. 3.4, б), представленные в иррациональных числах, которые выражают идеи роста, движения и развития. Непрерывное деление — основа их пропорциональных соотношений.

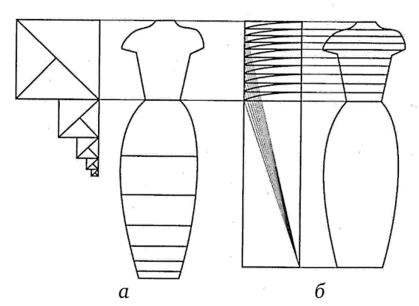
Рис. 3.4. «Квадраты Фибоначчи» с резким убыванием сторон (а) и «динамические прямоугольники» с постепенным убыванием сторон (б) Термин «золотое сечение» возник в связи с построением правильного пятиугольника (рис. 3.5), который включает в себя деление отрезка прямой на две неравные части, где целое так относится к большей части, как большая часть к меньшей. В некотором приближении отношения «золотого сечения» можно представить в виде ряда: 2/3, 3/5, 5/8, 8/13 и т. д. На рис. 3.6 представлены примеры часто встречающихся пропорциональных соотношений в композиции костюма.

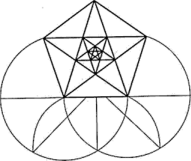
Рис. 3.5. Построение правильного пятиугольника.

Немецкий художник А. Дюрер тоже интересовался «золотым сечением» и построением правильных многоугольников. Его интерес отражался в использовании им пятиугольников в готических и арабских орнаментах, а также в планировке крепостей. Именно Дюрер передал средневековые, достаточно простые способы построения правильных многоугольников потомкам.

Великому математику Кеплеру принадлежит следующее высказывание о «золотом сечении»: «Геометрия обладает двумя великими сокровищами. Первое — это теорема Пифагора, второе — деление отрезка в среднем и крайнем отношении. Первое можно сравнить с мерой золота, второе назвать драгоценным камнем».

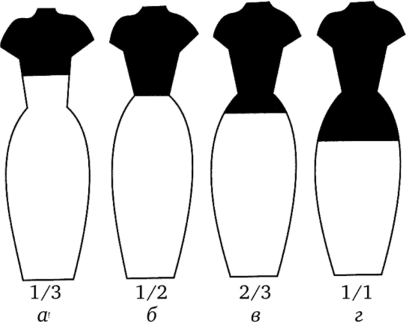
Рис. 3.6. Пропорциональные соотношения в композиции костюма: а — завышенная линия талии (1/3); б — линия талии на естественном месте, которая делит изделие пропорционально (½); в — линия талии чуть занижена (2/3); г — лиф и юбка одинаковы по длине (1/1).

Термин «золотое сечение» сформулировал немецкий ученый А. Цейзинг в XIX в. и дал ему следующие определения: 1) «золотое сечение» господствует в архитектуре; 2) «золотое сечение» господствует в природе; 3) «золотое сечение» господствует в архитектуре именно потому, что оно господствует в природе.

Немецкий математик Г. Вейль в своей книге «Симметрия» ограничивается следующим замечанием: «Это число является не чем иным, как отношением, известным под названием „золотое сечение“, играющим столь важную роль в попытках сведения красоты пропорций к некоторой математической формуле».

Но наряду с приверженцами теории «золотого сечения» существовали и критики этой теории. Один из самых влиятельных художественных критиков XIX в. Дж. Рёскин заявлял: «Определение хороших и дурных пропорций относится к компетенции вкуса и опыта в такой же мере, как и оценка качества музыкального сочинения». А в книге «Семь лампад архитектуры», вышедшей в 1849 г., Рёскин дал отрицательный отзыв об использовании пропорций в архитектуре, сравнив их с «расстановкой тарелок на обеденном столе».

Таким образом, из сказанного выше можно сделать вывод, что гармоничные пропорциональные соотношения основаны на неравенстве пропорций.

В моделировании одежды пропорции являются самым главным фактором в образовании формы. Простые пропорциональные соотношения выражаются дробным числом, где числитель и знаменатель — это целые числа от 1 до 8. Например, рукав ¾, мини-юбка 1/3, пальто 7/8, свитер 2/3 от целого. На рис. 3.7 приведены примеры встречающихся в моделировании пропорциональных соотношений, которые определяются интуитивно или задаются тенденциями моды. Каждое модное направление предлагает свои пропорциональные членения костюма и тем самым человека в костюме.

Рис. 3.7. Силуэты одежды пропорциональных соотношений в моде.

Ритм. Чередование каких-либо элементов (звуковых, речевых и т. п.), происходящее с определенной последовательностью, частотой, называется ритмом. Ритм был и есть во всех видах искусства во все времена. Уже в странах Древнего Востока композиция была упорядочена, отличалась строгостью и наличием ритма. В одежде древних ассирийцев использовался ритм бахромы, орнаментов и нашитых металлических пластин. У персов в одежде присутствовали орнаментированные и полосатые ткани разного ритма (рис. 3.8).

Рис. 3.8. Использование ритмов в одежде Древнего Востока: а — ассирийского воина; б — перса В древнеегипетском искусстве фриз являлся основной формой композиции, в которой ритмически чередовались изобразительные элементы. Ритмы прочитывались в нагрудных украшениях, ожерельях, в плиссированных одеждах (рис. 3.9).

Рис. 3.9. Использование ритмов в тканях и украшениях женской одежды.

Древнего Египта.

Рис. 3.10. Ритмы в драпированной одежде, орнаментах и украшениях Древней Греции (а) и Рима (б) Искусство Древней Греции, хорошо усвоившее явления ритма и симметрии, стало более живым по сравнению с искусством Египта: в росписях греческих ваз, в живописи, в скульптуре. Древнегреческая одежда вся была построена на различных ритмах складок и драпировок (рис. 3.10).

В средневековом искусстве явления ритма сохраняются (иранская миниатюра, где растительные мотивы образуют изысканные ритмические орнаменты). Появляются богато орнаментированные ткани со сложными раппортными рисунками. Ритмы прослеживаются в мужской стеганой одежде, в деталях металлических доспехов (рис. 3.11).

В эпоху Возрождения ритм считался одной из трех главных задач композиции: перспектива, ритмическое расчленение плоскости и точка зрения. Иллюстрацией этого были монументальные фрески и росписи храмов. В одежде этого времени присутствовали красивые ритмические складки плащей, сложные разнораппортные рисунчатые ткани, полосатые ткани штанов-чулок, множество декоративных разрезов. Много контрастных форм прочитывалось в мужской одежде: перепады форм, тяжелый, нагруженный отделками и накинутыми короткими плащами верх фигуры и неустойчивый низ с обтянутыми штанами-чулками (рис. 3.12). Одежда в основном была с вертикальной осью симметрии. Стеганая военная одежда была с ритмическими рядами стёжки и разрезов.

В XVIII—XIX вв. продолжается дальнейшее развитие ритмов в отделках, вышивках, в складках и плиссировках тканей, в сборках на юбках и плащах, в рядах пуговиц и петель.

В современной одежде ритм отделок, рисунков тканей и трикотажа, драпировок и складок применяется очень широко.

Рис. 3.11. Ритмы в одежде и в металлических доспехах воинов.

Средневековья.

Рис. 3.12. Ритмы в костюмах эпохи Возрождения.

В музыке, танце, поэзии ритм «разворачивается» во времени. В архитектуре, изобразительном и декоративно-прикладном искусстве его ощущение вызывается чередованием элементов или закономерным изменением свойств в определенном пространстве. Ритм служит для выражения упорядоченности, динамики и красоты, является одним из важнейших средств приведения многообразных или одинаковых элементов формы к гармоничному расположению.

Как уже было сказано, признаком ритма является повторяемость элементов формы и интервалов между ними на плоскости или в пространстве. Ритмические повторы одного и того же мотива или формы могут быть равномерными или неравномерными (нарастающими или убывающими).

Наиболее часто используется повторяемость двух типов: простая (статическая, или метрическая) и сложная (динамическая).

Статический ритмический ряд (или метрический ритм) — это простое проявление ритма с повторением в композиции одинаковых форм при равных интервалах между ними (рис. 3.13, а, б).

Рис. 3.13. Использование тканей с ритмическим рисунком в национальном (а) и современном (б) костюмах.

Динамический ритмический ряд — это сложное проявление ритма при изменяющихся с определенной математической закономерностью размерах элементов (мотивов) и интервалах между ними. Математической закономерностью может быть арифметическая или геометрическая прогрессия и т. д. Закономерность ритмического ряда может выражаться рядом натуральных чисел: 1, 2, 3, 4, 5, 6, 7. Закономерность ритмического ряда, построенного на прогрессии, может заключаться в сохранении постоянной разности между любыми соседними интервалами или в том, что величина каждого последующего элемента или интервала равна величине предыдущего, умноженной на постоянное число, например на два: 1 • 2 = 2; 2 • 2 = 4; 4 • 2 = 8; 8 • 2 = 16 и т. д. Динамический ритмический ряд предполагает следующие изменения:

• • увеличение или уменьшение элемента по величине при равных интервалах;
• • возрастание или убывание интервала по величине при равных по величине элементах;
• • возрастание или убывание по величине элементов и интервалов.

Закономерность построения ритмического ряда должна быть воспринимаемой. Основное правило прочтения ритмического ряда — обязательное, навязчивое повторение элемента или интервала не менее 3—5 раз. Число «три» (по старинным преданиям — магическое число) является тем минимальным числом, которое позволяет достаточно точно и четко определить любое разнообразие. Ритмическая организация даже простых геометрических элементов усиливает художественную выразительность и способна создавать определенное настроение. Эмоциональное воздействие ритмической композиции тем сильнее, чем активнее и разнообразнее применение различных ритмических построений.

Чередование равных по величине элементов выражает равномерное движение. В этом движении некоторые элементы выделяются зрительным «ударением» — акцентом. Элементы, на которые приходятся акценты, называются активными; элементы, не имеющие акцентов, — пассивными. Равномерное чередование активных и пассивных элементов называется метром. Расстояние от одного активного элемента до другого называется динамическим шагом.

Скорость нарастания движения элементов называется темпом. Темп может быть медленным, умеренным и быстрым. Для придания композиции большей выразительности применяют различные способы ускорения движения, усиления динамичности.

Ритм имеет огромное значение, так как определяет динамику формы, ее организованность и характер образа. В то же время выразительные возможности ритмических систем имеют свои пределы. Если в музыке бесконечно повторять одну и ту же ноту или в архитектуре строить архитектурную композицию на повторении только одного элемента, то неизбежна утомительная монотонность. Поэтому в композиции наряду с применением ритмических систем может присутствовать элемент случайности. Использование контраста между закономерностью ритма и случайным скоплением элементов чрезвычайно усиливает выразительность композиции.

Ритмы в костюме могут быть разного вида: лучевые, радиальные, спиральные, встречной направленности. На ритме в костюме строится очень многое:

• • складки, фалды, воланы, сборки;
• • ткань в полоску, клетку, с орнаментом, раппортные ткани (рис. 3.14, 3.15);

• • отделка кантом, защипами, буфами, оборками, строчками стежкой, вышивкой, бахромой, стеклярусом (рис. 3.16);
• • ритмические повторы слоев ткани;
• • застежки на пуговицы, кнопки, разнообразную фурнитуру, молнии, завязки, банты;
• • рельефы, орнаменты, резинки и пр.

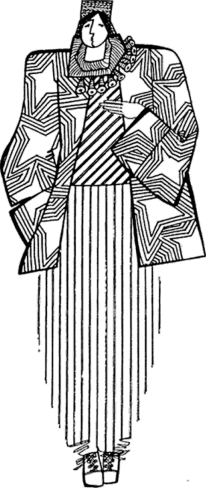
Рис. 3.14. Использование в костюме полосатых тканей с концентрическими ритмическими фигурами

Рис. 3.15. Применение материалов с ритмическими рисунками в колготках и обуви.

Рис. 3.16. Ритмы разных форм: кокетка (а) и воротник (б) нарядных блуз На рис. 3.17 показаны две модели стеганой одежды с элементами стилизации в духе русского и восточного национальных костюмов. В декоре использовано два разных вида ритмов: метрический и динамический.

Рис. 3.17. Эскизы моделей по мотивам восточного (а) и русского (б) национальных костюмов с ритмической обработкой декора.