Системы счисления. 
Системы счисления

Задание 1

• 1. Перевести двоичное число, А в шестнадцатеричную систему счисления, а из шестнадцатеричной системы — в десятичную.
• 2. Перевести шестнадцатеричное число С в двоичную систему счисления, а из двоичной системы — в десятичную.
• 3. Перевести десятичное число Е в двоичную систему счисления с абсолютной погрешностью, не превышающей 0,1.
• 4. Перевести десятичное число Q в двоично-десятичный код 8421, а число F из двоично-десятичного кода 8421 — в десятичную систему счисления.

Рассматриваемые числа А₍₂₎, С₍₁₆₎, Е₍₁₀₎, Q₍₁₀₎, F₍₂₋₁₀₎ приведены в табл.1.

Таблица 1.

Исходные числа к выполнению задания 1.

Решение.

1. Перевод двоичного числа в системы счисления с основаниями, кратными целой степени двойки, производится путем разбиения его на группы с соответствующим количеством разрядов, которые отсчитываются влево и вправо от точки, отделяющей целую и дробную части числа. Далее каждая группа представляется цифрой, соответствующей той системе счисления, в которую переводится число. Неполные крайние группы дополняются нулями.

Двоичное число 101.11 100 010 при переводе в шестнадцатеричную систему счисления разбивается на группы по четыре разряда (тетрады), а затем каждая тетрада заменяется цифрой шестнадцатеричной системы:

5 3 8 8.

Перевод чисел из шестнадцатеричной систем счисления в десятичную систему можно производить на основе представления числа в виде полинома от основания системы, из которой переводится число.

Целая часть Дробная часть Дробная часть.

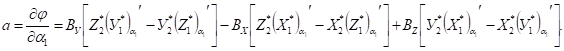
101.11 100 010 2 = = .

Ответ:; .

2.

Целая часть Дробная часть.

.

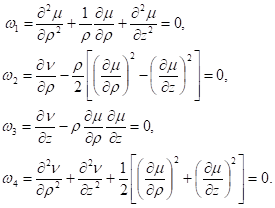
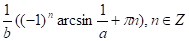
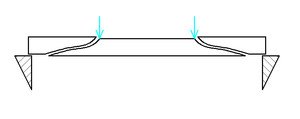
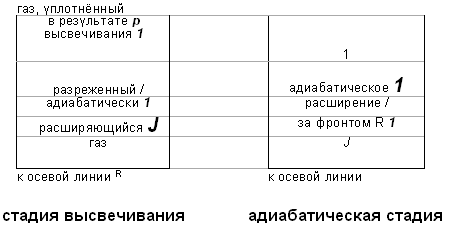
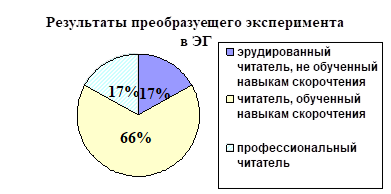
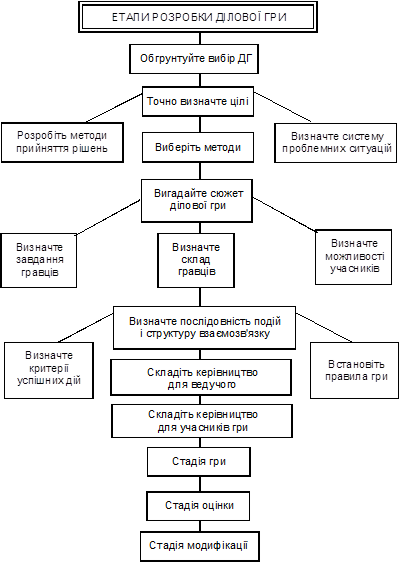
Ответ: .

3. Перевод десятичного числа 25.15 в двоичную систему счисления произведем раздельно для целой и дробной частей числа, а затем оба результата объединим в одно число двоичной системы счисления.

Так как при переводе дробей из десятичной системы счисления в двоичную можно получить дробь в виде бесконечного ряда, то задают необходимое количество разрядов m дробной части числа или абсолютную погрешность? результата перевода. Считая, что абсолютная погрешность числа определяется значением единицы младшего разряда, можно записать соотношение:

? > 2^-m (1).

Соответствующее количество разрядов числа можно определить из выражения:

m > log₂(1/?) / log₂2 (2).

В задании абсолютная погрешность результата перевода 0,1, отсюда находим.

m > log₂(1/0.1) / log₂2 > 3,32…

Округляя полученный результат до ближайшего большего целого числа, будем иметь m=4. Следовательно, при переводе можно ограничиться получением четырехразрядной двоичной дроби:

Ответ: 11 001.0010.

• 4. 853.8510 = 1000 0101 0011.1000 1 012−10
• 8 5 3 8 5

Для того чтобы перевести десятичное число 853.85 в двоично-десятичный код 8421 необходимо каждую десятичную цифру представить в виде двоичной тетрады (как в целой части числа, так и в дробной). При переводе числа 10 101 000 101 из двоично-десятичного кода 8421 — в десятичную систему счисления нужно заменить каждую двоичную тетраду соответствующей десятичной цифрой.

• 0101 0100 0101₂₋₁₀ = 545₁₀
• 5 4 5

Ответ: 853.85₁₀ = 100 001 010 011.10000101₂₋₁₀; 10 101 000 101₂₋₁₀ = 545₁₀.

Задание 2.

• 1. Записать в 8-разрядной сетке цифрового устройства в форме с фиксированной точкой двоичные числа, А и В.
• 2. Записать в 8-разрядной сетке в форме с плавающей точкой двоичное число С, выделив для мантиссы и порядка числа по четыре разряда (старшие разряды отводятся для мантиссы, младшие — для порядка числа).
• 3. Записать в 16-разрядной сетке, содержащей по восемь разрядов для мантиссы и порядка, двоичное число С в форме с плавающей точкой со смещенным порядком.
• 4. Записать в 8-разрядной сетке в прямом, обратном и дополнительном кодах двоичные числа, А и В.
• 5. Выполнить в 8-разрядной сетке логический, циклический и арифметический сдвиги на R разрядов вправо и влево двоичных чисел, А и В, приставив числа в прямом и дополнительных кодах.

Рассматриваемые числа А₍₂₎, В₍₂₎, С₍₂₎ и количество разрядов сдвига R приведены по вариантам в табл. 2.

Таблица 2.

Исходные числа к выполнению задания 2.

Решение.

1. — 101 100 111. Так как значения модулей целых двоичных чисел в 8-разрядной сетке не должны превышать значения 27 — 1 = 127 (заданное число равно 359), следовательно, ограничение на максимальное значение модуля не выполняется, произошло переполнение разрядной сетки, старшие разряды модуля теряются, и появляется ошибка в представлении числа. Заданное двоичное число в 8-разрядной сетке будет выглядеть таким образом (представляемое число отрицательное, значит, в знаковом разряде устанавливается 1):

0.101 111. Заданное число правильная дробь. Нуль в старшем разряде указывает на знак числа (положительный). Так как количество значащих цифр модуля меньше количества обозначенных для записи разрядов в сетке, то оставшийся свободным младший разряд заполняется нулем. Указанное двоичное число в 8-разрядной сетке с фиксированной точкой будет выглядеть следующим образом:

2. — 0.1. Представим число в нормализованной форме: — 0.1 = -0,1 • 2−4. Не поместившиеся в сетку значащие цифры модуля мантиссы теряются.

Тогда заданное двоичное число в 8-разрядной сетке с плавающей точкой будет выглядеть так:

3. — 0.1. Представим число в нормализованной форме: -0.1 = 0,1 • 2−4. Тогда с учетом формулы смещенного порядка:

Р _см = Р_д + 2 ^t-1, (3).

где Р_см — значение смещенного порядка;

Р_д — значение действительного порядка;

t — количество разрядов, используемых для размещения порядка в разрядной сетке.

Р _см = -4 + 2⁸⁻¹ = -4 + 128 = 124₁₀ = 1 111 100₂.

В итоге представление числа в рассматриваемой разрядной сетке будет иметь вид:

4. Прямой код: -101 100 111 = 1 101 100 111 и 0.101 111 = 101 111.

Запись в 8-разрядной сетке (так как значения модулей целых двоичных чисел в 8-разрядной сетке не должны превышать значения 2⁷ — 1 = 127, указанное число равно 359, следовательно, ограничение на максимальное значение модуля не выполняется, произошло переполнение разрядной сетки, старшие разряды модуля теряются):

обратный код: -101 100 111 = 1 010 011 000 и 0.101 111 = 101 111.

дополнительный код: -101 100 111 = 1 010 011 001 и 0.101 111 = 101 111.

5. Логический сдвиг: -101 100 111 и 0.101 111.

Прямой код:

Сдвиг влево на 3 разряда:

Сдвиг вправо на 3 разряда:

Дополнительный код:

Сдвиг влево на 3 разряда:

Сдвиг вправо на 3 разряда:

Циклический сдвиг: -101 100 111 и 0.101 111.

Прямой код:

Сдвиг влево на 3 разряда:

Сдвиг вправо на 3 разряда:

Дополнительный код:

Сдвиг влево на 3 разряда:

Сдвиг вправо на 3 разряда:

Арифметический сдвиг: -101 100 111 и 0.101 111.

Прямой код:

Сдвиг влево на 3 разряда:

Сдвиг вправо на 3 разряда:

Дополнительный код:

Сдвиг влево на 3 разряда:

Сдвиг вправо на 3 разряда:

Задание 3.

• 1. Вычислить S = A + B, представив слагаемые в формате байта с фиксированной точкой в дополнительном коде.
• 2. Вычислить Z = A + B, представив слагаемые в формате двух байт с плавающей точкой (старший байт для мантиссы, младший — для порядка числа).
• 3. Вычислить E = C + D, представив слагаемые в дополнительном двоично-десятичном коде 8421.
• 4. Вычислить П = А · В, используя алгоритм Бута, представив сомножители в формате байта с фиксированной точкой в дополнительном коде.
• 5. Вычислить Q = A: B, используя метод с неподвижным делителем без восстановления остатка, представив делимое и делитель в формате байта с фиксированной точкой.

Рассматриваемые числа А₍₁₀₎, В₍₁₀₎, С₍₁₀₎, D₍₁₀₎ приведены в табл. 3.

двоичный счисление алгоритм система Таблица 3.

Исходные числа к выполнению задания 3.

Решение.

1. Представим числа A = 6510 = 10 000 012 и B = -1110 = -10 112 в формате байта дополнительном коде: [А]доп = 1 000 001; [В]доп = 11 110 101.

Операции сложения полученных кодов чисел будут иметь вид:

[А]_доп = 1 000 001.

[В]_доп = 11 110 101.

Так как при сложении возникла единица переноса из знакового ряда, то она отбрасывается.

[S] _доп = 110 110.

[S] _пр = 110 110.

S = +110 110₂ = 54₁₀

Ответ: S = 65 + (-11) = 54.

2. Представим слагаемые в формате двух байтов с плавающей точкой в нормализованном виде: A = 6510 = 10 000 012 и B = -1110 = -10 112.

Определим разность порядков слагаемых, изменив знак порядка числа A (большего порядка) и представив порядки в дополнительном коде:

k [10 000 111]пр [11 111 001]доп.

+p [100]пр [100]доп.

(p — k) [11 111 101]доп [10 000 011]пр -11₂ = -3_10.

Исходя из полученного результата, произведем сдвиг мантиссы числа B на три разряда вправо:

М_B = М_{B, выр} = 10 001 011.

Произведем операцию сложения мантисс в дополнительном коде:

Поскольку в старшем разряде модуля суммы мантисс находится нуль, то необходимо провести нормализацию результата. Для этого модуль суммы мантисс сдвигается на один разряд влево при уменьшении порядка числа на единицу. Результат сложения рассматриваемых чисел в итоге будет иметь вид.

Z = 0.1 101 100 • 2⁶₂ = 110 110₂ = 54₁₀.

Ответ: Z = 65 + (-11) = 54.

3. Сформируем дополнительный код отрицательного числа:

C = -771₁₀ = -0111 0111 0001₂₋₁₀ > [1 0111 0111 0001]_пр,

Прибавим во все тетрады прямого кода корректирующую поправку:

После инверсии цифр в разрядах (кроме знакового) получим обратный код числа: [C]_обр =1 0010 0010 1000.

Дополнительный код получим путем прибавления единицы к младшему разряду обратного кода: [C]_доп = 1 0010 0010 1001.

Положительное число D = 231₁₀ = 0010 0011 0001₂₋₁₀ > [0 0010 0011 0001]_пр = [0 0010 0011 0001]_доп

Выполним операцию сложения дополнительных кодов чисел:

При суммировании получено отрицательное число (1 — в знаковом разряде), представленное в дополнительном коде. Для преобразования полученного результата в прямой код необходимо в каждую тетраду прибавить корректирующую поправку, затем нужно произвести инверсию цифр в тетрадах и прибавить единицу в младший разряд:

Ответ: E = -771 + 231 = -540.

4. A = 6510 = 10 000 012 и B = -1110 = -10 112 в формате байта дополнительном коде: [А]доп = 1 000 001; [В]доп = 11 110 101. Изменим знак числа A и представим его в дополнительном коде: [-A]доп = 10 111 111.

Последовательность выполняемых операций при умножении рассматриваемых чисел будет иметь такой вид:

Результат в дополнительном коде Преобразуя полученный результат в прямой код, в итоге получим:

[1 111 110 100 110 101]_доп > [1 000 001 011 001 011]_пр > -1 011 001 011₂ = -715_10.

Ответ: П = 65 • (-11) = -715.

A = 65₁₀ = 1 000 001₂ и B = -11₁₀ = -1011₂

5. Выполним деление числа A = 6510 = 10 000 012 [1 000 001]пр на число B = -1110 = -10 112 [10 001 011]пр. Знак частного определится так:

Знак Знак Знак делимого делителя частного.

0 1 = 1.

Представим модуль делителя в формате байта как положительное число в прямом коде и как отрицательное число в дополнительном коде, а модуль делимого в прямом коде с увеличенным в два раза количеством разрядов по отношению к делителю:

[|B|]_пр = 1 011; [-|B|]_доп = 11 110 101; [|A|]_пр = 1 000 001.

Операцию деления представим в следующем виде:

В результате за восемь циклов операции деления получена целая часть частного и положительный последний остаток.

Изменив знак в прямом коде модуля частного, в итоге получим:

[10 000 101]_пр > -101₂ = -5₁₀. Остаток — 1 010₂ = 10₁₀.

Ответ: Q = 65: (-11) = -5 (10 в остатке).

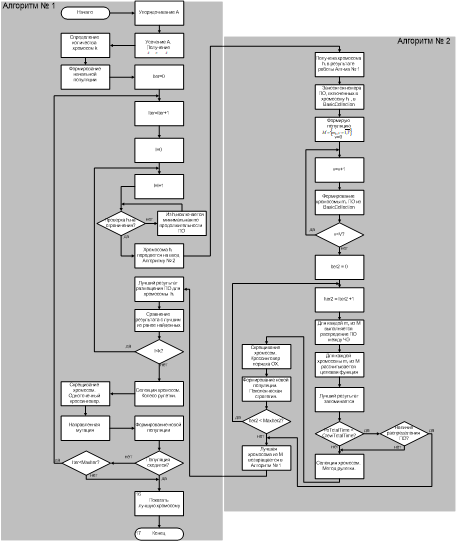
Задание 4.

• 1. Записать совершенную нормальную дизъюнктивную форму (СНДФ) логической функции, заданной в виде таблицы истинности.
• 2. Минимизировать СНДФ методом Квайна-Мак-Класки.
• 3. На основе минимальной формы логической функции построить схему комбинационного устройства, используя логические элементы И, ИЛИ, НЕ.
• 4. Перевести минимальную форму логической функции в инвертирующий базис И-НЕ.
• 5. Построить схему комбинационного устройства, используя только логические элементы И-НЕ.

Значения аргументов Х1, Х2, Х3, Х4 логической функции Y приведены по вариантам в табл.4.

Таблица 4.

Значения аргументов и логической функции к заданию 4.

Решение.

1. Функция Y принимает значение 1 для восьми наборов аргументов. Следовательно, СНДФ данной функции состоит из дизъюнкции восьми элементарных конъюнкций:

2. Перейдем к сокращенной форме логической функции. Для этого наборы аргументов в СНДФ представим их эквивалентами в двоичной форме:

Y = 0100? 0101? 0111? 1000? 1001? 1011? 1100? 1101.

Наборы аргументов в такой форме СНДФ объединяют в группы, содержащие одинаковое количество единиц. Для заданной логической функции объединение в группы представляло в столбце стадии I таблицы.

Определение сокращенной формы логической функции производится последовательно в несколько стадий путем выполнения операций попарного склеивания наборов.

Стадии определения сокращенной формы логической функции:

Y_сок = *01*? *10*? 1*0*? 01*1? *101? 10*1? 1*01? 110*.

Полученную форму можно представить и в виде логического выражения:

Переход от сокращенной формы логической функции к минимальной форме осуществляется при помощи импликантной матрицы:

Вычеркиваем.

0100? 0101? 0111? 1000? 1001? 1011? 1100? 1101.

Столбцы импликантной матрицы обозначены наборами аргументов СНДФ, а строки — простыми импликантами сокращенной формы логической функции. Крестиками в импликантной матрице пометим столбцы тех наборов аргументов СНДФ, которые поглощает каждая из простых импликант сокращенной формы. Таким образом, помечаются все столбцы матрицы. Затем обозначим столбцы, перекрываемые только одной импликантой. Такие существенные импликанты составляют ядро Квайна (Я) и не могут быть исключены из сокращенной формы. В данном случае имеется три существенных импликанты — *10*, 1*0* и 01*1 поскольку столбцы наборов 0100, 0111 и 1000 перекрываются только этими импликантами. Все столбцы, перекрываемые существенными импликантами, вычеркиваются. Далее выявляем минимальное количество импликант, не входящих в ядро, которые перекрывают оставшийся столбец матрицы. Этот столбец выделен цветом. Помечаем такие импликанты галочкой. С учетом импликант ядра, минимальную форму логической функции можно представить виде выражения:

3. Схема комбинационного устройства, построенная по минимальной форме логической функции с использованием логических элементов И, ИЛИ, НЕ, приведена на рис. 1.

4. Для перевода минимальной формы логической функции в инвертирующий базис И — НЕ дважды проинвертируем правую часть выражения:

Преобразуем полученное выражение, используя формулу де Моргана:

5. Полученному выражению соответствует схема комбинационного устройства, приведенная на рис. 2.