Особенности поляризации среды движущимся точечным зарядом

В нашей статье [4] описаны весьма необычные особенности поляризации среды прямолинейно движущимся точечным зарядом. Также как и в [4], здесь мы предположим, что поляризующаяся изотропная среда имеет собственные поляризационные колебания. Положим, что продольные колебания имеют частоту, а поперечные —. В таком случае диэлектрическая проницаемость среды, как показано в [5,6], будет зависеть от частоты действующего электрического поля по формуле:

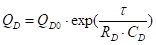
(1).

где — значение диэлектрической проницаемости на высоких частотах. Вследствие однородности среды не будет зависеть от местоположения рассматриваемой точки в пространстве. Выражение (1) очевидным образом согласуется с соотношением Лиддена-Сакса-Теллера.

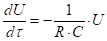
(2).

где — диэлектрическая проницаемость на частотах. Если на среду действует электрическое поле свободного (например, точечного) заряда с индукцией в точке с радиусом-вектором в момент времени, то напряженность электрического поля в среде. Фурье-образы по времени этих полей связаны между собой соотношением (в системе единиц СИ):

(3).

где — электрическая постоянная.

Для дальнейших расчетов удобно перейти от силовых полей и к их дивергенциям:

(4).

Тогда соотношение (3) превращается в связь фурье-компонент по времени соответствующих плотностей зарядов на частоте :

. (5).

Соотношение (5) удобнее тем, что в рассматриваемом случае движущихся зарядов проще задавать поле в виде, включающем несколько вариационных параметров для последующего согласования состояния движения свободного заряда с воздействием на него поляризационного заряда с плотностью поляризация точечный заряд спиновый.

. (6).

Таким образом, применяемый нами здесь метод в некоторой степени аналогичен вариационному методу нахождения основного состояния квантовомеханической системы.

Решение нашей задачи начинается с задания в цилиндрической системе координат функции.

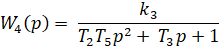
(7).

которая описывает вращение точечного заряда в плоскости, перпендикулярной оси вращения, с радиусом орбиты, частотой вращения, с отклонением от центра орбиты в плоскости вращения и угловой переменной. Переменные и являются вариационными параметрами. Причем, — функцию необходимо рассматривать как периодическую функцию своего аргумента. Ведь свободный заряд, вращаясь по окружности, с течением времени периодически оказывается в любой точке орбиты с заданным. Такую периодическую функцию для анализа удобно представить в виде разложения в ряд Фурье указаннойфункции, заданной на интервале изменения ее аргумента:

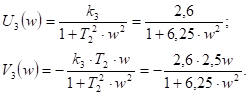
(8).

где — целое число.

Произведем Фурье-преобразование функции (7) по времени с заменой (8). В результате получим:

(9).

Следовательно, согласно (5).

(10).

а разность описывает плотность поляризационного заряда.

Для определения характера перемещения в пространстве поляризационного заряда произведем обратное Фурье-преобразование по функции (10). Прежде всего, отметим, что величина имеет особенность как функция частоты. Учитывая, что поляризационные колебания среды всегда затухают с течением времени, т. е., что их частоты имеют отрицательную мнимую часть интегрирование по частоте выполним методами функций комплексной переменной, считая, что величины бесконечно малы и положительны. В таком случае величину в (10) удобно представить в виде:

=. (11).

Поэтому после обратного Фурье-преобразования функции (10) одно слагаемое окажется отличающимся лишь множителем от выражения (7). Следовательно, плотность заряда будет включать плотность точечного заряда, расположенного в пространстве-времени также, как свободный заряд, но в раз меньшую по величине. Очевидно, что этот заряд представляет собой свободный заряд, экранированный высокочастотной поляризацией среды, описываемой параметром в выражении (1). Другая составляющая плотности распределения, соответствующая второму слагаемому в (11), никогда, насколько нам известно, не исследовалась в электродинамике сплошных сред со времен ее становления. Введем обозначение.

(12).

и рассчитаем, согласно (12), функцию.

. (13).

Интегрирование по в формуле (13) приводит к соотношению:

(14).

Для вычисления суммы по в (14) рассмотрим интеграл.

(15).

по окружности бесконечного радиуса в плоскости комплексного переменного, где.

. (16).

Функция имеет простые полюсы в точках с вычетами, равными единице. Функция.

(17).

при ведет себя как, то есть стремится к нулю при.

.

При она стремится к нулю при.

.

Следовательно, в основном интервале числитель подынтегрального выражения в (15) не растет, а, благодаря знаменателю, убывает быстрее, чем при по любому пути. Следовательно, интеграл (15) равен нулю по лемме Жордана и равна нулю сумма вычетов подынтегрального выражения в (15). Но сумма вычетов в полюсах функции, очевидно, равна сумме по в выражении (14). Кроме того, у множителя при в (15) имеется также два простых полюса. Таким образом, находим, что.

С учетом этого, вместо (14) получается выражение:

(19).

Таким образом, распределение оказывается одномерным, равным нулю вне орбиты свободного заряда. Может ли распределение своим воздействием обеспечить равномерное (с постоянной угловой скоростью) движение свободного заряда по орбите, не ускоряя и не замедляя его? Для ответа на этот вопрос рассмотрим знаки величины непосредственно перед движущимся по орбите свободным зарядом и непосредственно за ним, то есть при малом, но меньше 0, или малом, но больше 0. Эти знаки, оказывается, определяются величиной. Пусть, например,.

.

Тогда в обоих случаях будет близок к значению, а будет равен малому положительному или отрицательному значению. Таким образом, при плотность перед свободным зарядом и позади него на орбите будет различной. В такой ситуации на свободный заряд на орбите будет действовать сила, имеющая отличную от нуля тангенциальную составляющую. Следовательно, состояние вращения с не будет стационарным. Можно легко заметить, что тангенциальная составляющая силы, действующей на свободный заряд, исчезает только в том случае, если отношение является полуцелым или целым. Однако, при целом знаменатель в фигурной скобке в (19) обращается в ноль, а обращается в бесконечность. При полуцелом отношении.

плотность не имеет особенностей как функция :

где — целое число, включая 0, а, как указано выше, можно изменять в пределах от 0 до .

Частоты вращения при целом и полуцелом можно назвать частотами параметрического резонанса между орбитальным движением свободного заряда и колебаниями среды. Таким образом, полученное выше соотношение (19) фактически показывает, что в случае полуцелого возможно бесконечное повторение циклов равномерного вращения точечного свободного заряда вместе с поляризационным, распределенным по орбите (20).

Интересно, что в случае полуцелого интеграл по пространству от дает независящую от времени величину.

.

которая, с учетом соотношения Лиддена-Сакса-Теллера, в сумме с — образным зарядом дает величину. Такую же величину получают в электродинамике для покоящегося в среде заряда. Рассматриваемый здесь точечный заряд не совершает поступательного движения и поэтому имеет вместе с поляризационным зарядом величину. Мы считаем, что эта величина суммарного заряда подтверждает правильность выбранной модели и произведенных нами расчетов величины. В случае целого циклическое вращение свободного заряда наращивает при каждом цикле плотность, и с начала вращения при к любому конечному моменту она достигает бесконечной величины. Следовательно, при целом вращение не является стационарным в полном смысле слова. Этот случай аналогичен обычному резонансу, при котором в каждом цикле амплитуда колебаний маятника, увеличиваясь, стремится к бесконечности. Подробное исследование поступательного движения заряда в рассматриваемой среде с учетом квантовых эффектов описано в [4, 6, 7].

Формула (20) представляет зависимость значений от на орбите свободного заряда в случае.

при и. Согласно (20), плотность поляризационного заряда отлична о нуля только на орбите свободного заряда и в точке его расположения равна нулю. Вблизи этой точки она противоположна по знаку заряду. При величина достигает максимума при.

.

а при опять обращается в ноль. При изменение приводит к осцилляциям, но всегда в ближайшем окружении свободного заряда, то есть, при.

.

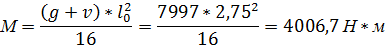
поляризационный заряд отрицателен. Вне этого интервала суммарный поляризационный заряд равен нулю. Следовательно, полный заряд на всей орбите и на интервале одинаков. Симметричные относительно точки.

элементы поляризационного заряда имеют одинаковые знак и величину. Следовательно, сила, действующая со стороны поляризационного заряда на свободный, будет центростремительной и одинаковой при любом. Таким образом, свободный заряд, поляризующий среду, способен совершать в однородной и изотропной среде стационарное вращательное движение по орбитам, радиусы которых могут быть найдены с помощью подгоночного параметра. Множество этих орбит, очевидно, будет дискретным, характеризуемым полуцелым «квантовым» числом. Свободный заряд на этих орбитах будет иметь момент импульса вращательного движения. Поскольку в рассматриваемой системе отсутствует силовой центр вращательного движения, то указанный момент импульса можно называть не орбитальным, а «спиновым».