Трехмерные матричные преобразования

Подобно тому, как двумерные преобразования описываются матрицами размером, трехмерные преобразования могут быть представлены матрицами размером. Тогда трехмерная точка записывается в однородных координатах как, где. Для получения декартовых координат надо первые три однородные координаты разделить на. Два однородных вектора описывают одну декартову точку в трехмерном пространстве, если, где и — векторы, записанные в однородных координатах.

Матрицы преобразований будем записывать в правосторонней системе координат. При этом положительный поворот определяется следующим образом. Если смотреть из положительной части оси вращения (например, оси) в направлении начала координат, то поворот на против часовой стрелки будет переводить одну положительную полуось в другую (ось в, в соответствии с правилом циклической перестановки).

Заметим, что на практике удобнее применять левостороннюю систему координат, так как в этом случае удобнее интерпретировать тот факт, что точки с большими значениями находятся дальше от наблюдателя.

Запишем теперь матрицу трехмерного переноса. Аналогично двумерному случаю.

.

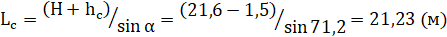
при этом.

.

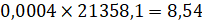
Операция масштабирования:

Перейдем к операции поворота, с ней в трехмерном случае придется разбираться чуть побольше чем в двумерном. Так как при двумерном повороте в плоскости координаты остаются неизменными, то поворот вокруг оси записывается так:

.

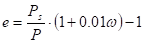
Матрица поворота вокруг оси имеет вид:

.

и вокруг оси :

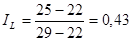
Обратите внимание на смену положения синуса угла с отрицательным знаком в матрице поворота вокруг оси. Правильность этих матриц легко проверить поворотом одного из ортов на, при этом он должен перейти в следующий по порядку орт на соответствующей координатной оси.

Обратные преобразования будут выражаться обратными матрицами. Для операции переноса надо лишь заменить знаки компонент вектора переноса на противоположные:

;

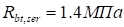
для операции масштабирования — на обратные значения:

;

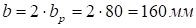
для поворота — выбором отрицательного угла поворота:

.

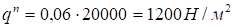
Результатом нескольких последовательных поворотов будет матрица.

.

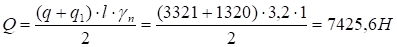
Здесь верхняя матрица размером называется ортогональной. Важным ее свойством является то, что обратная к ней матрица является транспонированной:. Это полезно тем, что при вычислениях достаточно поменять индексы местами и обратное преобразование получается автоматически.

После перемножения любого числа матриц вида и результирующая матрица всегда будет иметь вид:

.

Здесь верхняя часть размером определяет суммарный поворот и масштабирование, а три коэффициента последней строки — суммарный перенос.

Вопросы эффективности вычислений Рассмотрим проблему ускорения вычислений в одной из самых трудоемких операций компьютерной графики — операции поворота точки относительно начала координат. Как было показано ранее, для ее выполнения необходимо произвести 4 операции умножения, 2 операции сложения, а также вычислить значения синуса и косинуса угла поворота. Напомним вид формул поворота:

Одним из наиболее часто встречающихся способов ускорения операции поворота является отказ от вычисления синуса и косинуса угла во время выполнения программы, и использование их заранее подсчитанных значений, которые занесены в специальную таблицу. Например, в этой таблице могут храниться значения синусов и косинусов углов поворота с шагом в 1 градус. Тогда целое количество градусов угла поворота может служить в качестве индекса при извлечении соответствующих значений синусов и косинусов из таблицы. Такой прием называется табличным поворотом.

Дополнительным способом ускорения операции поворота является уменьшение количества операций умножения. Рассмотрим вывод формулы О. Бьюнемана с использованием тангенса половинного угла, в которой поворот точки вокруг начала координат производится за 3 операции умножения и 3 операции сложения. Так как на многих микропроцессорах операции умножения выполняются дольше чем операции сложения, то экономия времени достигается за счет уменьшения операций умножения.

Вывод формулы будем получать из геометрических построений, как показано на рис. 27.

Будем искать выражение координат и через и. На оси отложим отрезок, такой что. Тогда. Здесь отрезок является горизонтальной проекцией отрезка, где, ,, где. Теперь, зная, можно выразить в виде суммы длин отрезков и. Так как длины отрезков и равны как радиусы окружности с центром в точке, то. Обозначим, отсюда следует, что.

.

.

Последние три равенства будем называть формулой Бьюнемана Алгоритмы растровой графики Растром называется прямоугольная сетка точек, формирующих изображение на экране компьютера. Каждая точка растра характеризуется двумя параметрами: своим положением на экране и своим цветом, если монитор цветной, или степенью яркости, если монитор черно-белый. Поскольку растровые изображения состоят из множества дискретных точек, то для работы с ними необходимы специальные алгоритмы. Рисование отрезка прямой линии — одна из простейших задач растровой графики. Смысл ее заключается в вычислении координат пикселов, находящихся вблизи непрерывных отрезков, лежащих на двумерной растровой сетке.

Термин «пиксел» образован от английского pixel (picture element — элемент изображения) — то есть точка на экране. Будем считать, что пикселы имеют целочисленные координаты. На первый взгляд кажется, что эта задача имеет простое решение. Пусть конечные точки отрезка имеют целочисленные координаты, и уравнение прямой, содержащей отрезок:. Не нарушая общности, будем также считать, что тангенс угла наклона прямой лежит в пределах от 0 до 1. Тогда для изображения отрезка на растре достаточно для всех целых, принадлежащих отрезку, выводить на экран точки с координатами. Однако в этом методе присутствует операция умножения. Хотелось бы иметь алгоритм без частого использования операции умножения вещественных чисел. Избавиться от операции умножения можно следующим образом. Поскольку, то один шаг по целочисленной сетке на оси будет соответствовать. Отсюда получаем, что будет увеличиваться на величину. Итерационная последовательность выглядит следующим образом:

.

Когда, то шаг по будет приводить к шагу по, поэтому и следует поменять ролями, придавая единичное приращение, а будет увеличиваться на единиц. Этот алгоритм все же не свободен от операций с вещественными числами. Наиболее изящное решение задачи растровой развертки отрезков прямых было найдено Брезенхемом. В его алгоритме вообще не используются операции с вещественными числами, в том числе операции умножения и деления.

Для вывода формул алгоритма Брезенхема рассмотрим рис. 29.

Пусть начало отрезка имеет координаты, а конец. Обозначим,. Не нарушая общности, будем считать, что начало отрезка совпадает с началом координат, и прямая имеет вид, где. Считаем что начальная точка находится слева. Пусть нам шаге текущей точкой отрезка является. Выбор следующей точки или зависит от знака разности. Если, то и тогда, , если же, то и тогда, .

,.

.

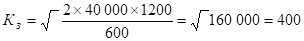
Поскольку знак совпадает со знаком разности, то будем проверять знак выражения. Так как и, то .

Пусть на предыдущем шаге, тогда и. Если же на предыдущем шаге, то и .

Осталось узнать как вычислить. Так как при :

.

Далее приводится листинг процедуры на языке Паскаль, реализующей алгоритм Брезенхема.

Procedure Bresenham (x1,y1,x2,y2,Color: integer);

var.

dx, dy, incr1, incr2,d, x, y, xend: integer;

begin.

dx:= ABS (x2-x1);

dy:= Abs (y2-y1);

d:=2*dy-dx;{начальное значение для d}.

incr1:=2*dy;{приращение для d<0}.

incr2:=2*(dy-dx);{приращение для d>=0}.

if x1>x2 then {начинаем с точки с меньшим знач. x}.

begin.

x:=x2;

y:=y2;

xend:=x1;

end.

else.

begin.

x:=x1;

y:=y1;

xend:=x2;

end;

PutPixel (x, y, Color);{первая точка отрезка}.

While x.

begin.

x:=x+1;

if d<0 then.

d:=d+incr1{выбираем нижнюю точку}.

else.

begin.

y:=y+1;

d:=d+incr2;{выбираем верхнюю точку, y-возрастает}.

end;

PutPixel (x, y, Color);

end;{while}.

end;{procedure}.

Перед тем, как исследовать методы получения изображений более сложных, чем отрезки прямых, рассмотрим проблему, незримо присутствующую в большинстве задач компьютерной графики. Эта проблема отсечения изображения по некоторой границе, например, по границе экрана, или, в общем случае, некоторого прямоугольного окна. Рассмотрим эту задачу применительно к отрезкам прямых. Некоторые из них полностью лежат внутри области экрана, другие целиком вне ее, а некоторые пересекают границу экрана. Правильное отображение отрезков означает нахождение точек пересечения их с границей экрана и рисование только тех их частей, которые попадают на экран. Один из очевидных способов отсечения отрезков состоит в определении точек пересечения прямой, содержащей отрезок, с каждой из четырех прямых, на которых лежат границы окна и проверки не лежит ли хотя бы одна точка пересечения на границе. В этом случае для каждой пары сторона-отрезок необходимо решать систему из двух уравнений, используя операции умножения и деления. При этом удобно параметрическое задание прямых:

.

Для эти уравнения определяют точки, находящиеся между и. Специальной проверки требует случай, когда отрезок параллелен стороне окна. Пусть координата x точки пересечения найдена, тогда.

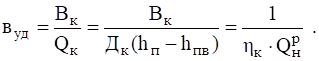
Рассмотрим алгоритм Коэна-Сазерленда для отсечения отрезков прямых. Этот алгоритм позволяет легко определять нахождение отрезка полностью внутри или полностью снаружи окна, и если так, то его можно рисовать или не рисовать, не заботясь об отсечении по границе окна.

Для работы алгоритма вся плоскость в которой лежит окно разбивается на девять подобластей или квадрантов, как показано на рис. 30.

Окну соответствует область обозначенная кодом 0000. Конечным точкам отрезка приписывается 4-битный код «вне/внутри» в зависимости от нахождения отрезка в соответствующей подобласти. Каждому биту присваивается значение 1 в соответствии со следующим правилом.

Бит 1 — точка находится выше окна;

Бит 2 — точка находится ниже окна;

Бит 3 — точка находится справа от окна;

Бит 4 — точка находится слева от окна;

Иначе биту присваивается нулевое значение. Значения этих битов для конечных точек отрезков легко определить по знакам соответствующих разностей: — для 1-го бита, — для 2-го бита, — для 3-го бита и — для 4-го бита. Отрезок рисуется без отсечения, то есть принимается целиком, если оба кода равны 0000, или ИЛИ, где ИЛИ — бинарная операция. Отрезок отбрасывается без вычислений если оба его конца находятся выше, ниже, правее или левее окна. В этих случаях соответствующие биты в обоих кодах равны 1 и это легко определить, умножив эти коды по бинарной операции И. Если результат операции И равен 0000, то отрезок нельзя ни принять ни отбросить, так как он может пересекаться с окном. В этом случае применяется последовательное разделение отрезка, так что на каждом шаге конечная точка отрезка с ненулевым кодом вне/внутри заменяется на точку, лежащую на стороне окна или на прямой содержащей сторону. При этом порядок перебора сторон окна не имеет значения.

Далее приводится текст процедуры на языке Паскаль, с довольно изящной реализацией этого метода. Отрезок задан граничными точками, , границы окна: xmin, xmax, ymin, ymax. Используются вызовы процедур: Accept_Check — выполняет проверку на полное принятие отрезка; Reject_Check — на полный отказ от рисования отрезка; Outcodes — вычисляет 4-х битовый код «вне/внутри»; SWAP — меняет местами координаты двух точек.

Procedure CLIP (x1,x2,y1,y2,xmin, xmax, ymin, ymax: real);

type.

outcode = array[1.4] of boolean;

var.

accept, reject, done: boolean;

outcode1,outcode2,.

outcode3,outcode4:outcode;{коды вне/внутри}.

begin.

accept:= false;

reject:= false;

done:= false;

repeat.

Outcodes (x1,y1,outcode1);

Outcodes (x2,y2,outcode2);

{проверка на отбрасывание}.

reject:=Reject_Check (outcode1,outcode2);

if reject then done:= true.

else.

begin {возможно принятие целиком}.

accept:=Accept_Check (outcode1,outcode2);

if accept then done:=true.

else.

begin {разделить отрезок}.

{если P1 внутри, то с помощью SWAP сделать снаружи}.

if not ((outcode1[1])or (outcode1[2])or.

(outcode1[3])or (outcode1[4])) then SWAP;

{теперь P1 перемещается в точку пересечения}.

if outcode1[1] then.

begin {отбросить верхнюю часть}.

x1:=x1+(x2-x1)*(ymax-y1)/(y2-y1);

y1:=ymax;

end.

else if outcode1[2] then.

if outcode1[1] then.

begin {отбросить нижнюю часть}.

x1:=x1+(x2-x1)*(ymin-y1)/(y2-y1);

y1:=ymin;

end.

else if outcode1[3] then.

begin {отбросить правую часть}.

y1:=x1+(y2-y1)*(ymax-x1)/(x2-x1);

x1:=xmax;

end.

else if outcode1[4] then.

begin {отбросить левую часть}.

y1:=x1+(y2-y1)*(ymin-x1)/(x2-x1);

x1:=xmin;

end;

end;

end;

until done;

if accept then.

Line (x1,y1,x2,y2); {нарисовать отрезок}.

end;{procedure}.