Поглощающие марковские цепи

Как указывалось выше, из поглощающего состояния нельзя перейти ни в какое другое, у поглощающих дискретных марковских цепей имеется множество, состоящее из одного или нескольких поглощающих состояний.

Для примера рассмотрим переходную матрицу, описывающую переходы в системе, имеющей 4 возможных состояния, два из которых являются поглощающими. Матрица перехода такой цепи будет иметь вид:

Практически важным является вопрос о том, сколько шагов сможет пройти система до остановки процесса, то есть поглощения в том или ином состоянии. Для получения дальнейших соотношений путем переименования состояний матрицу (1) переводят к блочной форме:

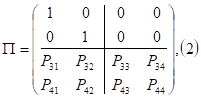
Такая форма позволяет представить матрицу (2) в каноническом виде:

.

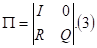
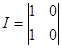
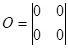
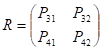
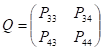
где — единичная матрица; - нулевая матрица; - матрица, описывающая переходы в системе из невозвратного множества состояний в поглощающее множество; - матрица, описывающая внутренние переходы в системе в невозвратном множестве состояний.

На основании канонической формы (3) получена матрица, называемая фундаментальной.. Матрица (4) — обратная матрица, то есть.

После соответствующих преобразований матрица (4) примет вид:

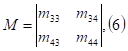
Каждый элемент матрицы (6) соответствует среднему числу раз попадания системы в то или иное состояние до остановки процесса (поглощения).

Если необходимо получить общее среднее количество раз попадания системы в то или иное состояние до поглощения, то фундаментальную матрицу М необходимо умножить справа на вектор-столбец, элементами которого будут единицы, то есть.

где.

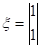
Для иллюстрации приведем конкретный числовой пример: пусть известны значения переходных вероятностей матрицы с одним поглощающим состоянием: P₁₁ = 1; P₁₂ = P₁₃ = 0; P₂₁ = 0,25; P₂₂ = 0,5; P₂₃ = 0,25; P₃₁ = 0,5; P₃₂ = 0,5; P₃₃ = 0.

Переходная матрица в блочной системе будет выглядеть так:

.

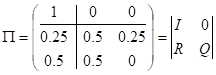
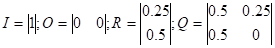
В данном случае. Проделаем необходимые вычисления:

;

;

.

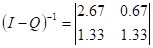
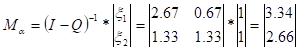
В данном случае компоненты вектора означают, что если процесс начался с состояния S₂, общее среднее число шагов процесса до поглощения будет равно 3,34 и, соответственно, если процесс начинается с состояния S₃, то — 2,26.

В конкретных задачах, конечно, более информативным результатом будет не количество шагов, а какие-либо временные или экономические показатели. Этот результат легко получить, если связать пребывание в каждом состоянии с соответствующими характеристиками. Очевидно, набор этих характеристик составит вектор, на который нужно умножить слева.

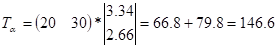
Так, если задать в нашем примере время пребывания в состоянии S₂ — t₂ = 20 час, а в состоянии S₃ — t₃ = 30 час, то общее время до поглощения будет равно: час.

В случаях, когда Марковская цепь включает несколько поглощающих состояний, возникают такие вопросы: в какое из поглощающих состояний цепь попадет раньше (или позже); в каких из них процесс будет останавливаться чаще, а в каких — реже? Оказывается, ответ на эти вопросы легко получить, если снова воспользоваться фундаментальной матрицей.

Обозначим через b_ij вероятность того, что процесс завершится в некотором поглощающем состоянии S_j при условии, что начальным было состояние S_i. Множество состояний b_ij снова снова образует матрицу, строки которой соответствуют невозвратным состояниям, а столбцы — всем поглощающим состояниям. В теории дискретных Марковских процессов доказывается, что матрица В определяется следующим образом:, где.

М — фундаментальная матрица с размерностью S;

R — блок фундаментальной матрицы с размерностью r.

Рассмотрим конкретный пример системы с четырьмя состояниями S₁— S₄, две из которых — S₁, S₂ — поглощающие, а две — невозвратные: S₃ и S₄. Для наглядности и простоты вычислений обозначим переходные вероятности следующим образом:

P₁₁ = P₂₂ = 1; P₃₁ = P₄₃ = q; P₃₄ = P₄₂ = P.

Остальные значения вероятностей будут нулевыми. Каноническая форма матрицы перехода в этом случае будет выглядеть так:

.

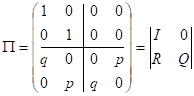
Фундаментальная матрица после вычислений примет вид:

.

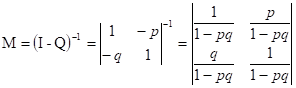
Тогда, согласно формуле (7), матрица вероятностей поглощения вычисляется так:

.

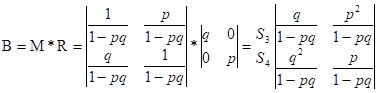
Поясним вероятностный смысл полученной матрицы с помощью конкретных чисел. Пусть p = 0,7, а q = 0,3. Тогда, после подстановки полученных значений в матрицу В, получим:

.

Таким образом, если процесс начался в S₃, то вероятность попадания его в S₁ равна 0,38, а в S₂ — 0,62. Отметим одно интересное обстоятельство: несмотря на то, что, казалось бы, левое поглощающее состояние («левая яма») находится рядом с S₃, но вероятность попадания в нее почти в два раза меньше, чем в «удаленную яму» — S₂. Этот интересный факт подмечен в теории дискретных Марковских процессов и объясняется он тем, что p? q, то есть процесс имеет как бы «правый уклон». Рассмотренная выше модель называется в теории дискретных Марковских процессов моделью случайного блуждания. Такими моделями часто объясняются многие физические и технические явления и даже поведение игроков во время различных игр.

В частности, в рассмотренном примере объясняется факт того, что более сильный игрок может дать заранее значительное преимущество («фору») слабому противнику и все равно его шансы на выигрыш будут более предпочтительными.

Кроме указанных выше средних характеристик вероятностного процесса с помощью фундаментальной матрицы можно вычислить моменты и более высоких порядков. В частности, дисперсия числа пребывания в том или ином состоянии — D определяется с помощью следующей матрицы:

.

где.

— диагональная матрица, т. е. матрица, полученная из М путем оставления в ней лишь диагональных элементов и замены остальных элементов нулями. Например, приведенная выше матрица (6) будет иметь вид:

.

В свою очередь, матрица представляет собой матрицу, полученную из М путем возведения в квадрат каждого ее элемента, то есть для (6) будем иметь:

.