Представление кривых линий

Параметризация кривых. При геометрическом моделировании фигуры, инцидентные кривым в пространстве, являются конечными отсеками этих кривых. Рассматриваемое множество точек кривой является образом непрерывного кусочно-обратимого отображения замкнутого отрезка числовой прямой. Отображаемый отрезок называется областью изменения параметра, а само отображение — параметризацией. Одна и та же кривая может быть па-раметризирована бесчисленным множеством способов. Параметризация осуществляется заданием декартовых координат текущей точки кривой как функций некоторого параметра:

х = х (t), у = у (/), z = z (t), а < t < b. (4.6).

Конкретный вид этих функций отличает данную параметризацию от всех прочих. Известно, что если t = t (и) — произвольная непрерывная и строго монотонная функция, то.

x = x (t (и)) = х (и), у = у (t (u)) = у (и), z = z (t (и)) = z (и) (4.7).

— другая параметризация той же кривой. И наоборот, если (4.6) и х = х (и), у = у (и), г = z (и) (4.8).

— две различные параметризации одной кривой, то существует единственная непрерывная и строго монотонная функция t = t (и), переводящая одну параметризацию в другую по формуле (4.7).

Заметим, что область значений такой функции — тоже отрезок. Подобные функции реализуют непрерывное и взаимно однозначное отображение отрезка на отрезок. Ясно, что обратная функция и = и (t) переводит вторую параметризацию в первую.

Будем пользоваться параметрическим уравнением кривой в векторной форме.

r = r (t) = х (t) е₁ + у (t)e₂ + z (t)e₃ (4.9).

где r = {х, у, г] — радиус-вектор текущей точки на кривой; e_l, e₂, e₃ — орты координатных осей.

Кривая называется m раз непрерывно дифференцируемой, если она допускает т раз непрерывно дифференцируемую параметризацию. Непрерывно дифференцируемые кривые (т = 1), допускающие параметризацию, первая производная которой всюду отлична от нуля (| r' | Ф 0), называются гладкими. Для них в каждой точка кривой определен касательный вектор. Если при некотором t выполняется равенство | r' (t) = 0, то точка может быть особой. Кусочно-гладкие кривые в инженерной геометрии обычно рассматриваются как составные, т. е. для каждого гладкого куска вводится своя параметризация.

Рассматриваемые кривые будем предполагать гладкими и обладающими кусочно-непрерывной ограниченной кривизной, г. с. допускающими такую параметризацию r = r (t), что вторая производная r" (f) кусочно-непрерывна и ограничена.

Сформулированные выше условия выделяют из всех кривых сравнительно узкий класс Q, который включает кривые, используемые в инженерной геометрии. Несмотря на довольно жесткие математические ограничения, этот класс оказывается вполне достаточным для практических целей.

Дискретно-точечным заданием кривой будем называть конечную совокупность {r_i i=1,2, …, N} точек кривой, упорядоченных по ее длине. В некоторых из них могут быть заданы дополнительные сведения о свойствах кривой в окрестности соответствующей точки. Такой способ представления сложных кривых в инженерной практике является обычным. При его использовании предполагается наличие некоторого инструмента для интерполирования. Физической реализацией такого инструмента является, например, упругая рейка. В качестве математического «инструмента» используются различные функции, чаще всего полиномы Лагранжа, Ньютона, сплайны. Известно, что для конкретного дискретно-точечного задания кривой и любой возрастающей числовой последовательности t₁ < t₂ < … < t_N можно найти (и притом не единственным образом) такую параметризацию r = r (t), t Ј [t_lt t_N] > этой кривой, что r (t₁) — r_i для всех i. Следовательно, задача об интерполировании кривой по ее дискретно-точечному заданию может быть сведена к интерполированию какой-либо параметризации, т. е. некоторой вектор-функции.

Решению задач такого рода посвящены целые разделы вычислительной математики [5; 9; 16; 19; 23; 24]. Рассмотрим некоторые аспекты геометрического моделирования кривой по ее дискретно-точечному каркасу [24]. Ограничимся представлением кривых с помощью кубических параметризованных кривых вида.

Почему рассматриваются именно кубические кривые? Потому что для сегментов кривой не существует представления более низкого порядка, которое обеспечивало бы в точке соединения кривых друг с другом непрерывность положения и наклона сегментов и в то же время гарантировало бы, что концевые точки сегмента кривой проходят через заданные точки. Отметим, что основная цель — описать кривую с помощью последовательности сегментов кривой (рис. 10). В точке соединения сегменты кривой и их касательные векторы равны. Эта непрерывность имеет важное значение.

Для описания непрерывности используется следующее обозначение С. Предположим, что кривые С" непрерывны, если они не имеют разрывов. В общем случае С⁽ⁱ⁾— непрерывность означает, что непрерывны функция и ее первые I производные.

Параметрический кубический многочлен с четырьмя коэффициентами является параметрической кривой наиболее низкой степени, которая при соответствующем выборе коэффициентов может удовлетворять четырем условиям (положению каждого из концов сегмента и касательным векторам в них). Можно использовать также параметрическое представление и более высокого уровня, однако в этом случае появляется волнистость и возникают осцилляции. Кубический многочлен является, кроме того, параметрической функцией наиболее низкой степени, с помощью которой можно представить неплоскую кривую, необходимую для описания пространственных кривых.

Ниже подробно рассмотрены три способа описания параметрических бикубических кривых: метод Эрмита, в котором задаются положения конечных точек кривой и касательные векторы в них; метод Безье, в котором задается положение конечных точек кривой) а для неявного задания касательных в этих точках используются две другие точки, обычно лежащие не на кривой; метод В-сплайнов, при котором конечные точки не лежат на кривой, в результате чего как первая, так и вторая производные оказываются непрерывными на концах сегмента. Каждая из этих трех форм описания кривой имеет свои достоинства и недостатки.

Форма Эрмита. Зададим точки Р₁ и Р₄ и касательные векторы r₁ и R₄ (точкам присваиваются индексы 1 и 4, а не 1 и 2 для совместимости с выражениями, которые используются при построении кривых методами Безье и В-сплайнов). Требуется найти коэффициенты а?, аг, аз и а* из выражения (4.10), удовлетворяющие условиям.

x (0) = x_lt х (1)=х" х'(0) = х, *(!) = *;, (4.11).

где индекс х означает ссылку на ^ - компоненты точек и касательных векторов.

Переписывая выражение для х (t), получим.

Чтобы записать выражение для ограничений на касательные векторы, продифференцируем сначала выражение (4.13) по t и получим, обращая матрицу размером 4×4, получим искомое выражение для С_x

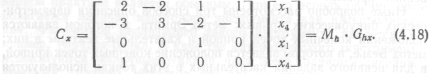
Здесь через Mh обозначена эрмитова матрица, а через Ghx — геометрический вектор Эрмита. Подставляя этот результат в выражение (4.13), получим.

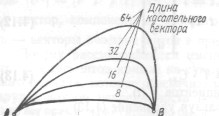
Рис. 10.

Четыре функции переменной t в произведении (4.22) называют функциями сопряжения, так как с помощью первых двух функций сопрягаются точки r₁ и r₄, а посредством двух других — векторы r₁ и r₄, в результате чего получается сглаженное объединение r (t).

Рис. 11.

На рис. 10 приведен ряд эрмитовых кривых. Их геометрические матрицы отличаются друг от друга только длиной касательного вектора. Чем больше длина вектора, тем сильнее кривая вытягивается в направлении, задаваемом этим вектором до того, как он начнет перемещаться к противоположному концу сегмента. Во всех случаях касательные к кривым имеют в концевых точках одно и то же направление. На рис. 11 показан другой ряд эрмитовых кривых — длина касательного вектора остается неизменной, а изменяется направление.

Форма Безье. Эта форма описания кубической кривой близка к эрмитовой форме, однако отличается от нее заданием касательных векторов в конечных точках. В форме Безье используются четыре точки (рис. 12). Касательные векторы в конечных точках задаются отрезками Р₁P₂ и P₄P₃. В частности, касательные векторы r₁ и r₄ эрмитовой формы определяются так, чтобы соответствовать четырем точкам Безье P_l P₂, P₃ и P₄:

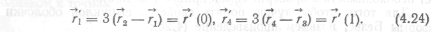
Поэтому соотношение между геометрической матрицей Эрмита и геометрической матрицей Безье G_b записывается.

Подставляя (4.25) в выражение (4.23), найдем.

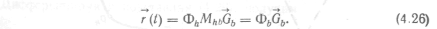
Обозначив произведение Ф_hМ_hb через Ф_b, получим выражение r (t) = Ф_bС_b которое имеет форму Безье. Матрицу М_b, полученную на рис. 13 приведены две кривые Безье, имеющие общую конечную точку P₄ Непрерывность первого порядка в этой точке гарантируется в том случае, если Р₃Р₄ = k * P₄P₅.

Форма Безье благодаря двум своим свойствам используется в машинной графике чаще, чем эрмитова форма. Во-первых, потому, что геометрическая матрица (в случае четырех точек) интуитивно привлекательна в интерактивном режиме, так как, перемещая точки с помощью локатора, можно легко привести кривую к желаемой форме. В случае эрмитовой формы касательные векторы должны задаваться в явном виде; в режиме диалога их определять труднее, да и само понятие производной не знакомо некоторым пользователям. Однако, если касательный вектор известен, то привести кривую в соответствие с ним легче при использовании эрмитовой формы. Во-вторых, четыре управляющие точки определяют выпуклый многоугольник (выпуклую оболочку), внутри которого находится кривая Безье (см. рис. 12).

Рис. 12.

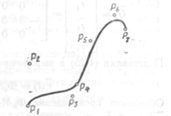
Рис. 13.

Выпуклая оболочка точек на плоскости есть область, задаваемая резиновой нитью, которая натянута вокруг всех точек (или в случае трех измерений область, задаваемая резиновой мембраной, плотно облегающей все точки). Выпуклая оболочка оказывается полезной при отсечении кривой по окну или видимому объему. Вместо того, чтобы сразу проводить отсечение кривой, сначала проверяется ее выпуклая оболочка, и только в том случае, если она пересекает окно или видимый объем, возникает необходимость в проверке самой кривой.

Для того, чтобы лучше понять свойство выпуклой оболочки формы Безье, возьмем произведение (4.26):

Исследуя коэффициенты многочлена при четырех точках, находим, что каждый из них изменяется в диапазоне 0…1, а сумма их равна 1 для всех 0 ^ t ^ 1. Это выражение описывает взвешенное среднее значение для четырех управляющих точек. Можно показать, что взвешенное среднее для п точек попадает внутрь выпуклой оболочки п точек.

Форма В-сплайнов. Кривая, представленная в виде кубического В-сплайна, в общем случае может проходить через любые управляющие точки, однако она непрерывна и, кроме того, непрерывностью изменения обладают ее касательный вектор и кривизна (т. е. первая и вторая производные кривой непрерывны в конечных точках) в отличие от форм Эрмита и Безье, у которых в конечных точках непрерывны лишь первые производные, проходящие через управляющие точки. Таким образом, можно утверждать, что форма В-сплайнов более гладкая, чем другие формы. Термин сплайны происходит от длинных гибких металлических реек, с помощью которых чертежники размечают поверхности самолетов и кораблей. Металлические сплайны, если они не сильно напряжены, обладают непрерывностью второго порядка. В-сплайн описывается формулой.

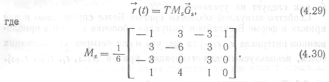
При аппроксимации управляющих точек r_ъ r₂, …, r_п последовательностью В-сплайнов будем применять между парой соседних точек геометрические матрицы. Для аппроксимации в интервале,.

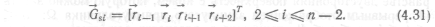
Покажем теперь непрерывность первой и второй производных в точке r_i+i. Подставляя в выражение (4.29) G_s = G_si и t = 1, имеем.

Аналогично, дифференцируя выражение (4.29) и подставляя t = = 1, получим.

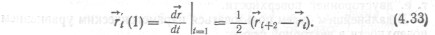
Дифференцируя и подставляя (4.29), получим.

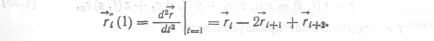
близком к точкам r_i и r_i+1, используем.

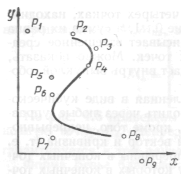
Рис. 14.

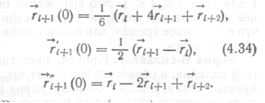
Выражения для [ж, у, з} - координат двух сегментов кривых и первых двух производных в месте соединения при условии r_t (1) = r_i+1 (0) совпадают.

Из приведенных выражений видно, что соединения точек и их производных являются взвешенными суммами трех ближайших соседних точек. На рис. 14 показана аппроксимация нескольких точек с помощью В-сплайнов. Поскольку точки 5, 6 и 7 имеют одинаковое значение координаты х, кривая проходит через точку, значение х которой совпадает со значением этой координаты точки 6, как следует из уравнения (4.32).

Свойство выпуклой оболочки кривых Безье справедливо и для кривых в форме В-сплайнов: выпуклая оболочка кривой в приближенном интервале {r_i, r_i+1} та же, что и для четырех управляющих точек, используемых для генерации кривой {r_i-1, r_i, r_i+1, r_i+2}.