Как классифицировать стержневые системы по кинематическому признаку?

Их можно подразделить на три категории: геометрически изменяемые или механизмы, у которых перемещения узлов не связаны с деформированием элементов; геометрически неизменяемые или же кинематически неподвижные, у которых перемещения узлов возможны только при условии деформирования элементов; мгновенно изменяемые.

По статическому критерию стержневые системы делятся на статически определимые и статически неопределимые. У первых усилия во всех элементах, включая опорные связи, определяются исключительно при помощи одних уравнений равновесия. Все остальные системы отнесем к классу статически неопределимых.

Что такое кинематический анализ расчетных схем?

Его основная цель — выяснить, является ли заданная стержневая система геометрически неизменяемой, т. е. пригодной для использования в строительстве. Для ответа на поставленный вопрос вначале устанавливают степень свободы расчетной схемы W.

Как вычислить степень свободы?

Русским ученым П. Л. Чебышевым получена формула, позволяющая это сделать. Для подсчета W для рамных систем она имеет такой вид:

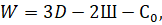
где D — число жестких дисков системы, впервые упомянутых на стр.4;

Ш — число простых соединительных шарниров, упомянутых на стр.3;

С₀ — число опорных стержней (см. раздел, посвященный опорным связям).

Алгоритм использования вышеупомянутой формулой достаточно прост. Покажем это на примере рамы на рис. 10,а. Для определения числа жестких дисков D заданную систему мысленно рассекают по соединительным шарнирам и «отбрасывают» опорные закрепления (рис. 10,б). Очевидно, что D= 3. Далее, для определения Ш в заданной системе ликвидируют опорные закрепления, оставив при этом шарнирные соединения (рис. 10,в). Заметим, что соединительный шарнир, А объединяет 3 жестких диска и его кратность числу простых шарниров Ш=3−1=2; шарниры В и С — простые, объединяющие каждый по 2 диска. Итак, общее число простых соединительных шарниров системы Ш=2+1+1=4. Число опорных стержней в соответствии с условиями закрепления данной рамы (см. стр.3 и 4) С₀= 1+2+3=6. Степень свободы W = 3Ч3 -2Ч4 — 6 = -5.

Проведем анализ возможных результатов вычисления степени свободы W по формуле Чебышева. Если W ?0, это означает, что система геометрически изменяема и по определению не может служить расчетной схемой строительной конструкции. При W? 0 система имеет избыточное число связей и является статически неопределимой, но ничего определенного этот результат не дает касательно ее геометрической неизменяемости. При W=0 система статически определима. Но, как и в предыдущем случае, это не является гарантией ее геометрической неизменяемости. Поэтому вторым шагом исследования расчетной схемы сооружения является ее структурный анализ. Он базируется на приведении расчетной схемы сооружения к простейшим видам двухи трехдисковых сочленений. Заметим при этом, что опорная поверхность (или «земля») может быть рассмотрена в качестве отдельного жесткого диска. Итак:

• 1. Система геометрически неизменяема, если жесткий диск крепится к земле с помощью трех стержней, линии действия которых не пересекаются в одной точке (рис.11).
• 2. Два жестких диска формируют геометрически неизменяемую систему, если они объединены шарниром и стержнем, линия действия которого не проходит через ось шарнира (рис.12).
• 3. Три жестких диска образуют геометрически неизменяемую систему, если они соединены тремя шарнирами, не лежащими не одной прямой. Частным случаем является шарнирный треугольник (рис.13).

Каковы основные допущения, принятые в классической строительной механике?

• — концепция линейнодеформируемой системы. В ее рамках — допущения об идеальной упругости материала и малости перемещений. Все это сконцентрировано в понятии относительной жесткости — когда деформации элементов и перемещения любых их точек существенно малы по отношению к их наименьшему линейному размеру. Отсюда возникает понятие о расчете по недеформируемой схеме, когда не делают разницы между деформированным состоянием системы под нагрузкой и его первоначальным недеформированным состоянием;
• — принцип независимости действия сил, смысл которого заключается в том, что эффект от действия какой-либо системы нагрузок равен сумме эффектов от действия каждой нагрузки, действующей независимо от других.

СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ.

РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ НА НЕПОДВИЖНУЮ НАГРУЗКУ.

Изучению основных свойств и методов расчета статически определимых систем придается огромное значение в общей теории расчета стержневых систем.

Как известно, поле напряжений в произвольном сечении стержневой системы может быть приведено к трем силовым факторам: продольной силе N, поперечной (перерезывающей) силе Q и изгибающему моменту М. На рис. 14 показаны направления этих усилий принятых положительными на примере балочного горизонтального элемента. Что касается изгибающего момента, в строительной механике при построении его эпюры действует такое правило: эпюра М располагается (или «откладывается») со стороны т.н. растянутых волокон, понятие которых вводится еще в курсе сопротивления материалов.

Полный статический расчет стержневой системы состоит в определении как внутренних усилий (М, Q и N) и усилий в опорных связях, так и перемещений (деформаций) системы. Важнейшим свойством статически определимых систем является то, что перечисленные выше задачи являются невзаимосвязанными. Поэтому тепловое воздействие и кинематическое смещение опор не приводят к деформированию систем и возникновению в них внутренних усилий.

Сконцентрируем наше внимание на применении к расчету подобных систем статического метода. Он базируется на применении независимых уравнений равновесия, полученных в курсе теоретической механики в разделе «Статика».

Все дальнейшие успехи в освоении начального курса строительной механики связаны с уверенным и стабильным умением строить эпюры изгибающих моментов в различных типах стержневых систем. Напомним, что «эпюрой» какого-либо внутреннего усилия называют график (схему, рисунок, диаграмму) зависимости величины этого усилия от рассматриваемого сечения какого-либо элемента системы. Определение величин изгибающих моментов, а также поперечных и продольных сил производится с помощью метода сечений. Введем понятие т.н. «характерного участка». Отметим, что изменение величин изгибающих моментов и поперечных сил в различных сечениях по длине элемента происходит по разным законам и зависит от характера внешних нагрузок и вида опорных закреплений. Применительно к некому линейному участку, его можно разделить на отдельные (характерные) участки, в пределах которых моменты и поперечные силы меняются по постоянному для выбранного участка закону.

Границами таких участков являются сечения, в которых приложены сосредоточенные силы, моменты, расположены различные опоры, а также сечения, где начинает и заканчивает свое действие равномерно-распределенная нагрузка или меняется ее интенсивность (рис.15).

Границами характерных участков для балки на рис. 15 являются сечения 1,2,3,4,5,6,7 и 8, а самими характерными участкамиэлементы этой балки 1−2, 2−3, 3−4, 4−5, 5−6, 6−7 и 7−8.

Что понимается под табличными эпюрами изгибающих моментов?

Это определение охватывает три наиболее характерные эпюры в консольной балке — стержне, жестко закрепленном с одного своего конца и свободном на другом. Приложим на его свободном конце последовательно сосредоточенную силу Р, сосредоточенный момент m, а также загрузим консольную балку равномерно-распределенной нагрузкой q.

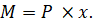
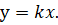
Запишем выражение для момента силы Р относительно моментной точки k, выбранной произвольно на расстоянии x от свободного края балки: Из курса аналитической геометрии нам известно уравнение прямой, проходящей через начало координат: Отсюда — однозначный вывод: эпюра от данного вида нагрузки очерчена по прямой, проходящей через две особые точки: при x=0 — M=0, а при x=L — М=РЧL. Очертание изогнутой оси консольной балки при данном силовом воздействии приведено на рис. 17. Из анализа рисунка следует, что в данном случае растянутыми являются верхние волокна, а посему эпюра М будет расположена также сверху от нейтральной оси балки (рис.18).

2. Далее рассмотрим, как выглядит эпюра изгибающих моментов в консольной балке при приложенном на ее свободном конце сосредоточенном моменте m (рис.19).

Проведем сквозное сечение 1−1 через точку k и рассмотрим равновесие отсеченной части балки (которая, как-бы, «висит» в воздухе). Запишем выражение для суммы моментов всех внешних и внутренних сил, действующих на отсеченный участок, относительно точки k.

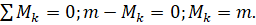
Так как выбор точки для проведенного сечения был произвольным, делаем вывод о постоянстве величины искомого изгибающего момента по всей длине балки. Очертание изогнутой оси консольной балки при данном силовом воздействии приведено на рис. 20. Из анализа рисунка следует, что и в данном случае растянутыми являются верхние волокна, а посему эпюра М будет расположена также сверху от нейтральной оси балки (рис.21).

3. «Загрузим» консольную балку равномерно-распределенной нагрузкой q (рис.22). Заметим, что под ее интенсивностью q понимается нагрузка, приходящаяся на единицу длины балки.

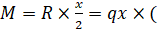
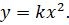
Проведем сквозное сечение 1−1 через точку k и рассмотрим равновесие отсеченной части балки (которая, как-бы, «висит» в воздухе). Заменим равномерно-распределенную нагрузку на участке длиной x ее равнодействующей R=qЧx (рис. 23,а) и вычислим момент этой равнодействующей относительно точки k: x/2)= qx²/2. Из курса аналитической геометрии известно, что уравнение квадратной параболы, проходящей через начало координат, выглядит аналогично: Следовательно, эпюра моментов в нашем случае очерчена по квадратной параболе с двумя характерными точками: при x=0 — М=0, а при x=L — M=qL²/2. Очертание изогнутой оси консольной балки при данном силовом воздействии приведено на рис. 23,б. Из анализа рисунка следует, что в данном случае растянутыми являются верхние волокна, из-за чего эпюра М должна быть расположена сверху от нейтральной оси балки.

При построении данной криволинейной эпюры дополнительно надо определить ее характер, т. е. «выпуклая» она или же «вогнутая». На этот вопрос легко ответить, применив т.н. «правило паруса». Оно базируется на простой аналогии с вогнутостью реального паруса под действием ветра:

Итак, при действии равномерно-распределенной нагрузки эпюра моментов очерчена по квадратной параболе с выпуклостью, совпадающей с направлением действия этой нагрузки .

На рис. 24 изображена эпюра изгибающих моментов при действии равномерно-распределенной нагрузки на консольную балку.

qL²/2.

На базе трех полученных выше «табличных» случаев продолжим расчет консольных балок на действие различных сочетаний нагрузок для приобретения элементарных практических навыков в построении эпюр изгибающих моментов.

Пример 1.

Анализ предложенной задачи приводит к следующим выводам:

• — данная конструкция является консольной балкой;
• — определение опорных реакций в такой конструкции необязательно;
• — построение эпюры моментов следует начинать со свободного конца;
• — число характерных участков равно двум (см. стр.10).

Пронумеруем границы характерных участков для лучшего усвоения предлагаемого алгоритма построения эпюры изгибающих моментов. Расчет начинаем с участка 1−2. Для этого прибегнем к такому приему — мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис. 25,а). При этом участок 1−2 становится аналогом первого частного случая (см. рис.18), поэтому характер эпюры и величина изгибающего момента правее точки 2 известны (рис. 25,б).

На следующем шаге ликвидируем условную заделку правее сечения 2 и переставляем ее в сечение 3 (рис26,а). При этом балка в сечении 2 восстанавливает свои кинематические характеристики. Далее рассмотрим участок 2−3. Приложим к нему сосредоточенный момент М=9, отложенный выше нейтральной оси в сечении, правее т.2 (см. рис. 25,б) и растягивающий, таким образом, верхние волокна. Кроме того, на участок 2−3 переносим сосредоточенную силу Р₂=3, прикладываем ее в точке 2 (рис. 26,б) и добавляем сосредоточенную силу Р₁= 7. Определим равнодействующую двух вертикальных сил в сечении 2: R = P₁-P₂= 7−3= 4 (рис. 26,в). Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 3. Независимое действие М=9 соответствует частному случаю 2 (рис.21), приводя к растяжению верхних волокон. Отложим ординату 9 выше нейтральной оси (рис. 26,г); независимое действие сосредоточенной силы R=4 приводит к растяжению нижних волокон (по аналогии с частным случаем 1 на рис.18). А величина созданного ею момента в заделке 3 равна М₃=РЧL=4Ч4=16. Отложим эту ординату ниже нейтральной оси. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 3 равна М₃=16−9=7. Этот момент растягивает нижние волокна. В пределах характерного участка 2−3 эпюра изгибающих моментов прямолинейна. Результат проведенного расчета на участке 2−3 — на рис. 26,д. На рис. 26, е изображена полная эпюра моментов для рассмотренного случая загружения консольной балки системой сосредоточенных сил.

Обратим внимание на характерную особенность полученной эпюры в сечении 2. При действии сосредоточенной силы на эпюре изгибающих моментов в этом сечении наблюдается перелом (или же излом) в сторону действия этой нагрузки. Это свойство широко применяется при визуальном контроле правильности построения эпюры изгибающих моментов.

Пример 2.

Анализ новой задачи вновь приводит к таким выводам:

— данная конструкция является консольной балкой;

• — определение опорных реакций в такой конструкции необязательно;
• — построение эпюры моментов следует начинать со свободного конца;
• — число характерных участков равно двум (см. стр.10).

Вновь пронумеруем границы характерных участков. Расчет начинаем с участка 1−2. Для этого вновь прибегнем к уже известному приему — мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис. 27,а). При этом участок 1−2 становится аналогом второго частного случая (см. рис.21), поэтому характер эпюры и величина изгибающего момента правее точки 2 известны (рис. 27,б).

На следующем шаге вновь ликвидируем условную заделку правее сечения 2 и переставляем ее в сечение 3 (рис28,а). При этом балка в сечении 2 восстанавливает свои кинематические характеристики. Далее рассматриваем участок 2−3. Приложим к нему сосредоточенный момент М=17, отложенный выше нейтральной оси в сечении правее т.2 (см. рис. 27,б) и растягивающий, таким образом, верхние волокна. Кроме того, на участке 2−3, прикладываем в точке 2 (рис. 28,б) сосредоточенную силу Р₁=7. Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 3. Независимое действие М=17 соответствует частному случаю 2 (рис.21), приводя к растяжению верхних волокон. Отложим ординату 17 выше нейтральной оси (рис. 28,в); независимое действие сосредоточенной силы Р₁=7 приводит к растяжению нижних волокон (по аналогии с частным случаем 1 на рис.18). А величина созданного ею момента в заделке 3 равна М₃=РЧL=7Ч4=28. Отложим эту ординату ниже нейтральной оси. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 3 равна М₃=28−17=11. Этот момент растягивает нижние волокна. В пределах характерного участка 2−3 эпюра изгибающих моментов прямолинейна. Результат рассмотрения участка 2−3 — на рис. 26,г. На рис. 26, д изображена полная эпюра моментов для рассмотренного случая загружения консольной балки системой нагрузок.

При визуальном контроле построенной эпюры с удовлетворением отмечаем наличие перелома под действием сосредоточенной силы Р₁, что указывает на правильность наших действий.

Анализ новой задачи вновь приводит к таким выводам:

— данная конструкция является консольной балкой;

• — определение опорных реакций в такой конструкции необязательно;
• — построение эпюры моментов следует начинать со свободного конца;
• — число характерных участков равно двум (см. стр.10).

Вновь пронумеруем границы характерных участков. Расчет начинаем с участка 1−2. Для этого вновь прибегнем к уже ставшему стандартным приему — мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис. 29,а). При этом участок 1−2 становится аналогом первого частного случая (см. рис.18), поэтому характер эпюры и величина изгибающего момента правее точки 2 известны (рис. 29,б).

На следующем шаге ликвидируем условную заделку правее сечения 2 и переставляем ее в сечение 3 (рис30,а). При этом в сечении 2 восстанавливаются ее кинематические характеристики. Далее рассмотрим участок 2−3. Приложим к нему сосредоточенный момент М=12, отложенный ниже нейтральной оси в сечении правее т.2 (см. рис. 30,б) и растягивающий, таким образом, нижние волокна. Кроме того, на участок 2−3 переносим сосредоточенную силу Р=4, прикладываем ее в точке 2 (рис. 30,б) и добавляем внешний сосредоточенный момент М=18.

Определим равнодействующую двух моментов в сечении 2: М_R = 18−12= 6 (рис. 30,в). Результирующий момент левее сечения 2 растягивает верхние волокна. Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 3. Независимое действие М_R=6 соответствует частному случаю 2 (рис.21), приводя к растяжению, как было отмечено только что, верхних волокон. Отложим ординату 6 выше нейтральной оси (рис. 30,г); независимое действие сосредоточенной силы Р=4 приводит к растяжению нижних волокон (по аналогии с частным случаем 1 на рис.18). А величина созданного ею момента в заделке 3 равна М₃=РЧL=4Ч4=16. Отложим эту ординату ниже нейтральной оси. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 3 равна М₃=16−6=10. Этот момент растягивает нижние волокна. В пределах характерного участка 2−3 эпюра изгибающих моментов прямолинейна. Результат проведенного расчета на участке 2−3 — на рис. 30,д. На рис. 30, е изображена полная эпюра моментов для рассмотренного случая загружения консольной балки системой нагрузок.

Отметим третий прием визуального контроля правильности построения эпюры изгибающих моментов: при действии сосредоточенного момента на эпюре М наблюдается «скачок» на его величину при одновременном сохранении ее наклона до и после его приложения. Все это нашло отражение на рис. 30,е.

Пример 4.

Анализ предложенной задачи приводит к следующим выводам:

• — данная конструкция является консольной балкой;
• — определение опорных реакций в такой конструкции необязательно;
• — построение эпюры моментов следует начинать со свободного конца;
• — число характерных участков равно двум (см. стр.10).

Пронумеруем границы характерных участков. Расчет начнем с участка 1−2. Для этого вновь прибегнем к уже ставшему стандартным приему — мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис. 31,а). При этом эпюра на участке 1−2 является аналогом второго частного случая (см. рис.21), ее характер и величина изгибающего момента правее точки 2 известны (рис. 31,б).

На следующем стандартном шаге ликвидируем условную заделку правее сечения 2 и переставляем ее в сечение 3 (рис32,а). При этом в сечении 2 восстанавливаются ее кинематические характеристики. Далее рассмотрим участок 2−3. Приложим к нему сосредоточенный момент М=9, отложенный ниже нейтральной оси в сечении правее т.2 (см. рис. 32,б) и растягивающий, таким образом, нижние волокна. Кроме того, на участке 2−3 (рис. 32,б) добавляем равномерно-распределенную нагрузку интенсивностью q = 2.

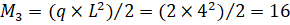
Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 3. Независимое действие М=9 соответствует частному случаю 2 (рис.21), приводя к растяжению, как было отмечено только что, нижних волокон. Отложим ординату 9 ниже нейтральной оси (рис. 32,г); независимое действие равномерно-распределенной нагрузки q=2 приводит к растяжению верхних волокон (по аналогии с частным случаем 3 на рис.24). А величина созданного ею момента в заделке 3 равна. Отложим эту ординату выше нейтральной оси. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 3 равна М₃=16−9=7. Этот момент растягивает верхние волокна. В пределах характерного участка 2−3 эпюра изгибающих моментов очерчена по квадратной параболе выпуклостью вниз. Результат проведенного расчета на участке 2−3 — на рис. 32,д. На рис. 32, е изображена полная эпюра моментов для рассмотренного случая загружения консольной балки системой нагрузок.

Пример 5.

Анализ предложенной задачи приводит к выводам, неоднократно обозначенным выше:

• — данная конструкция является консольной балкой;
• — определение опорных реакций в такой конструкции необязательно;
• — построение эпюры моментов следует начинать со свободного конца;
• — число характерных участков равно двум (см. стр.10).

Пронумеруем границы характерных участков. Расчет начнем с участка 1−2. Для этого вновь прибегнем к уже ставшему стандартным приему — мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис. 33,а). При этом эпюра на участке 1−2 является аналогом третьего частного случая (см. рис.24), ее характер и величина изгибающего момента правее точки 2 известны (рис. 33,б).

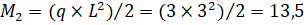
На следующем стандартном шаге ликвидируем условную заделку правее сечения 2 и переставляем ее в сечение 3 (рис34,а). При этом в сечении 2 восстанавливаются ее кинематические характеристики. Далее рассмотрим участок 2−3. Приложим к нему сосредоточенный момент М=13,5, отложенный выше нейтральной оси в сечении правее т.2 (см. рис. 34,б) и растягивающий, таким образом, верхние волокна. Также в сечение 2 переносим «скрытую» поперечную силу R, равную R = qЧL= 3Ч3=9. Кроме того, на участке 2−3 (рис. 34,б) в сечении 2 добавляем сосредоточенный момент М = 9.

Упростим полученную систему нагрузок, действующих на участок 2 — 3, вычислив равнодействующую двух сосредоточенных моментов М_R = 15 — 13,5 = 1,5. Этот момент растягивает нижние волокна.

Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 3. Независимое действие сосредоточенного момента М=1,5 соответствует частному случаю 2 (рис.21), приводя к растяжению, как было отмечено только что, нижних волокон. Отложим ординату 1,5 ниже нейтральной оси (рис. 34,г); независимое действие сосредоточенной R=2 приводит к растяжению верхних волокон (по аналогии с частным случаем 1 на рис.18). А величина созданного ею момента в заделке 3 равна PЧL= 9Ч2= 18. Отложим эту ординату выше нейтральной оси. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 3 равна М₃=18−1,5=16,5. Этот момент растягивает верхние волокна. В пределах характерного участка 2−3 эпюра изгибающих моментов прямолинейна. Результат проведенного расчета на участке 2−3 — на рис. 34,д. На рис. 34, е.

изображена полная эпюра моментов для рассмотренного случая загружения консольной балки заданной системой нагрузок.

Пример 6.

Анализ предложенной задачи приводит к выводам, неоднократно обозначенным выше:

• — данная конструкция является консольной балкой;
• — определение опорных реакций в такой конструкции необязательно;
• — построение эпюры моментов следует начинать со свободного конца;
• — число характерных участков равно двум (см. стр.10).

Пронумеруем границы характерных участков. Расчет начнем с участка 1−2. Для этого вновь прибегнем к уже ставшему стандартным приему — мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис. 35,а). При этом эпюра на участке 1−2 является аналогом третьего частного случая (см. рис.24), ее характер и величина изгибающего момента правее точки 2 известны (рис. 35,б).

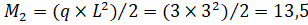
На следующем стандартном шаге ликвидируем условную заделку правее сечения 2 и переставляем ее в сечение 3 (рис36,а). При этом в сечении 2 восстанавливаются ее кинематические характеристики. Далее рассмотрим участок 2−3. Приложим к нему сосредоточенный момент М=13,5, отложенный выше нейтральной оси в сечении правее т.2 (см. рис. 36,б) и растягивающий, таким образом, верхние волокна. Также в сечение 2 переносим «скрытую» поперечную силу R, равную R = qЧL= 3Ч3=9. Кроме того, на участке 2−3 (рис. 34,б) в сечении 2 добавляем сосредоточенную силу Р = 7.

Упростим полученную систему нагрузок, действующих на участок 2 — 3, вычислив равнодействующую двух сосредоточенных сил R = 12 — 9= 3 (рис. 36,в).

R=qЧL=3Ч3=9.

Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 3. Независимое действие сосредоточенного момента М=13,5 соответствует частному случаю 2 (рис.21), приводя к растяжению, как было отмечено выше, верхних волокон. Отложим ординату 13,5 выше нейтральной оси (рис. 36,г); независимое действие сосредоточенной R=3 приводит к растяжению нижних волокон (по аналогии с частным случаем 1 на рис.18). А величина созданного ею момента в заделке 3 равна PЧL= 3Ч4= 12. Отложим эту ординату ниже нейтральной оси. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 3 равна М₃=13,5−12=1,5. Этот момент растягивает верхние волокна. В пределах характерного участка 2−3 эпюра изгибающих моментов прямолинейна. Результат проведенного расчета на участке 2−3 — на рис. 36,д. На рис. 36, е.

изображена полная эпюра моментов для рассмотренного случая загружения консольной балки заданной системой нагрузок.

Пример 7.

Пронумеруем границы характерных участков. Расчет начнем с участка 1−2. Для этого вновь прибегнем к уже ставшему стандартным приему — мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис. 37,а). При этом эпюра на участке 1−2 является аналогом первого частного случая (см. рис.18), ее характер и величина изгибающего момента правее точки 2 известны (рис. 37,б).

На следующем стандартном шаге ликвидируем условную заделку правее сечения 2 и переставим ее в сечение 3 (рис38,а). При этом в сечении 2 восстанавливаются ее кинематические характеристики. Далее рассмотрим участок 2−3. Приложим к нему сосредоточенный момент М=21, отложенный ниже нейтральной оси в сечении правее т.2 (см. рис. 38,б) и растягивающий, таким образом, нижние волокна. Также в сечение 2 переносим сосредоточенную силу Р=7. Кроме того, на участке 2−3 (рис. 38,б) добавляем равномерно-распределенную нагрузку интенсивностью q = 3.

Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 3. Независимое действие сосредоточенного момента М=21 соответствует частному случаю 2 (рис.21), приводя к растяжению нижних волокон. Отложим ординату 21 ниже нейтральной оси (рис. 38,в); независимое действие сосредоточенной Р=7 приводит к растяжению нижних волокон (по аналогии с частным случаем 1 на рис.18). А величина созданного ею момента в заделке 3 равна PЧL= 7Ч4= 28. Отложим эту ординату ниже нейтральной оси. Воздействие равномерно-распределенной нагрузки на участок 2−3 приводит к возникновению изгибающего момента, растягивающего верхние волокна (по третьему частному случаю) и равного М=qЧL²/2=3Ч4²/2=24. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 3 равна М₃=21+28−24=25. Этот момент растягивает нижние волокна. В пределах характерного участка 2−3 эпюра изгибающих моментов должна быть очерчена по квадратной параболе с выпуклостью вниз. Результат проведенного расчета на участке 2−3 (пока без построенной эпюры) — на рис. 36,г. расчетный сооружение консольный эпюра На этом рисунке пунктиром показаны два варианта прохождения криволинейной эпюры М через точки с ординатами 25 и 21 — либо по пологой кривой, либо по кривой, имеющей точку экстремума. Для конкретизации характера поведения данной эпюры обратим свои взоры к еще одному важному разделу расчета стержневых систем, а именно, к процессу построеня эпюры поперечных сил.

Как построить эпюру поперечных сил по имеющейся эпюре изгибающих моментов?

В основе данной процедуры лежит известное нам соотношение, вытекающее из теоремы Журавского, а именно:

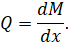
Смысл этого соотношения в том, что поперечная сила Q является первой производной по моменту M. Напомним, что геометрический смысл первой производной — это тангенс угла наклона ц касательной t, проведенной в расчетной точке (рис.39).

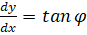
В рамках предлагаемой процедуры следует различать два случая:

• — эпюра изгибающих моментов — прямолинейна;
• — эпюра изгибающих моментов криволинейна (рассмотрим случай очертания эпюры по квадратной параболе).

Построение эпюры Q в случае прямолинейности эпюры М.

В этом случае, как это видно из рис. 40, касательная, проведенная в любой точке произвольного фрагмента прямолинейной эпюры М, имеет одинаковый угол наклона относительно нейтральной оси. Что означает, по сути, постоянство поперечной силы Q на участке с прямолинейным очертанием эпюры М.

Используя это соображение, рассмотрим четыре «табличных» случая построения эпюры поперечных сил. Но, прежде всего, дадим правило знаков для поперечной силы, которая, как известно из курса сопротивления материалов, двузначна.

Эпюра Мпрямоугольник с ординатой b. б) Эпюра М — прямоугольный треугольник.

Построение эпюры Q в случае, если эпюра М очерчена по квадратной параболе.

Пусть эпюра моментов очерчена по квадратной параболе, длина этого участка L, интенсивность равномерно-распределенной нагрузки q, она действует в направлении «сверху-вниз», ординаты этого фрагмента по краям участка, соответственно, а и b (рис.41).

Используя принцип суперпозиции (или же закон наложения), представим фигуру на рис. 41 следующим образом:

Следует заметить, что эпюры, показанные на рис. 42,б, соответствуют загружению однопролетной балки длиной L системой двух сосредоточенных моментов a и b, приложенных по ее краям, а также равномерно-распределенной нагрузкой q. Двум этим составляющим эпюрам поставим в соответствие эпюры Q, характер и значения которых нам известны (табличный случай «в» на стр. 27, а также характерная эпюра в виде «бабочки», известная из курса сопромата).

А затем на основе принципа суперпозиции, сложив две эти эпюры, получим искомую эпюру Q на участке с криволинейным очертанием эпюры M.

Вернемся к рис. 38,г примера 7 и попробуем построить эпюру поперечных сил на «спорном» участке. Знак «минус» для Q из односторонней трапеции — за счет совмещения нейтральной оси с эпюрой против часовой стрелки.

Изменение знака Q с «плюса» на «минус» указывает на наличие точки перегиба на участке 2−3 эпюры М, изображенной на рис. 43 и построенной для примера 7. Поперечная сила на участке 1−2 построена в соответствии со случаем «а» на стр. 27, знак поперечной силы — «минус» — определен совмещением нейтральной оси с эпюрой М против часовой стрелки.

Построение эпюр внутренних усилий в консольных рамах.

Что понимается под формулировкой «рама»?

Это — стержневая конструкция, в состав которой входят как т.н. «жесткие» (рис. 44,а), так и «шарнирные» узлы (рис. 44,б). При деформировании строительных конструкций жесткие узлы сохраняют свою первоначальную геометрию (чего нельзя сказать о узлах шарнирных), свободно перемещаясь на плоскости при отсутствии препятствующих этому связей.

Что такое «консольная рама»?

Это рама, имеющая в своем составе только жесткие узлы и прикрепленная к основанию с помощью жесткой заделки. При расчете рам к эпюрам изгибающих моментов М и поперечных сил Q добавляются эпюры продольных сил N.

Пример 8.

Следует сразу заметить, что в рамах границами характерных участков становятся также и узловые точки.

Анализ предложенной задачи приводит к выводам, неоднократно обозначенным выше:

• — данная конструкция является консольной;
• — определение опорных реакций в такой конструкции необязательно;
• — построение эпюры моментов следует начинать со свободного конца;
• — число характерных участков равно двум (см. стр.10).

Вновь пронумеруем границы характерных участков. Расчет начинаем с участка 1−2. Для этого вновь прибегнем к уже ставшему стандартным приему — мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис. 45,а). При этом участок 1−2, очевидно, находится под действием системы нагрузок Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении правее точки 1. Независимое действие сосредоточенного момента М=5 соответствует частному случаю 2 (рис.21), приводя к растяжению нижних волокон. Отложим ординату ниже нейтральной оси (рис. 45,б); независимое действие сосредоточенной силы Р=7 приводит к растяжению верхних волокон (по аналогии с частным случаем 1 на рис.18). А величина созданного ею момента в заделке 1 равна PЧL= 7Ч2= 14. Отложим эту ординату выше нейтральной оси. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 1 равна М₁=14−5=9. Этот момент растягивает верхние волокна. В пределах характерного участка 1−2 эпюра изгибающих моментов прямолинейна. Результат проведенного расчета на участке 1−2 — на рис. 45,в.

Для перехода на вертикальный участок 2−3 необходимо «уравновесить» узел 2, т. е. добиться, чтобы сумма моментов, как внутренних, так и приложенных снаружи внешних (если они есть), относительно оси узла 2 была бы равна нулю. Для этого «вырежем» узел 2 с помощью замкнутого сечения и приложим к нему известный момент в сечении правее точки 2, равный 9, растягивающий верхние волокна, что следует из рис. 45,в, и вращающий узел по часовой стрелке. Искомый момент M_x в сечении ниже точки 2 в этом случае также равен 9, но вращает узел в противоположном направлении, т. е. против часовой стрелки (рис. 46,а). Обратим внимание на тот факт, что полученный из равновесия узла 2 момент, равный 9, растягивает левые волокна на стойке 2−3.

На следующем стандартном шаге ликвидируем условную заделку правее сечения 2 и переставим ее в сечение 3 (рис46,б). При этом в сечении 2 восстанавливаются ее кинематические характеристики. Далее рассмотрим участок 2−3. Приложим к нему сосредоточенный момент М=9, полученный из равновесия узла и отложенный слева от нейтральной оси. Также к участку 2−3 прикладываем равномерно-распределенную нагрузку q=2 (рис. 46,в).

Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 3. Независимое действие сосредоточенного момента М=9 соответствует частному случаю 2 (рис.21), приводя к растяжению левых волокон. Отложим ординату 9 левее нейтральной оси (рис. 46,в). Воздействие равномерно-распределенной нагрузки на участок 2−3 приводит к возникновению изгибающего момента, растягивающего правые волокна (по третьему частному случаю) и равного М=qЧL²/2=2Ч4²/2=16. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 3 равна М₃=16−9=7. Этот момент растягивает правые волокна. В пределах характерного участка 2−3 эпюра изгибающих моментов должна быть очерчена по квадратной параболе с выпуклостью влево. Результат проведенного расчета на участке 2−3 — на рис. 46,г.

На рис. 47,а показана полная эпюра изгибающих моментов для рассматриваемого случая нагружения, а на рис. 47,в — эпюра поперечных сил, построенная в соответствии с принципами, изложенными на стр. 27 и 28 (рис. 47,б).

Как построить эпюру продольных сил N ?

Эпюра продольных сил строится по эпюре поперечных сил Q с помощью вырезания узлов. Для этого нам следует применить следующий алгоритм:

• — вырезать узел при помощи замкнутого сечения с эпюры Q (начинать эту процедуру следует с двухстержневого узла), на рис. 47,в это — узел 2;
• — начертить вырезанный узел и приложить к стержням положительно направленные искомые продольные силы (в направлении «от узла»), известные поперечные силы (имея в виду, что положительные поперечные силы вращают узел по часовой стрелке и наоборот), а также узловые силы при их наличии (рис. 48,а);
• -

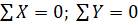
используя известные уравнения статики (), определить величины и знаки искомых продольных сил. Эпюра продольных сил приведена на рис. 48,б.

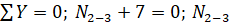
= -7.

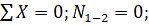
Пример 8.

Сначала пронумеруем границы характерных участков. Обратим внимание на то, что мы впервые сталкиваемся с трехстержневым узлом 4. Наметим вначале последовательность нашего расчета. Вначале рассмотрим участок 1−2, затем перейдем на участок 2−4 и вычислим величину изгибающего момента в сечении выше точки 4. Затем рассчитаем участок 3−4 и вычислим момент в сечении правее точки 4. Далее «вырежем» узел 4 и определим величину момента левее точки 4. В завершение расчета рассмотрим участок 4−5. Расчет начинаем с участка 1−2. Для этого вновь прибегнем к уже ставшему стандартным приему — мысленно установим в сечении, совпадающем с окончанием первого участка, жесткую заделку (рис. 49,а). При этом эпюра на участке 1−2 является аналогом первого частного случая (см. рис.18), ее характер и величина изгибающего момента левее точки 2 известны (рис. 49,б).

Для перехода на вертикальный участок 2−4 необходимо «уравновесить» узел 2, т. е. добиться, чтобы сумма моментов, как внутренних, так и приложенных снаружи внешних (если они есть), относительно оси узла 2 была бы равна нулю. Для этого «вырежем» узел 2 с помощью замкнутого сечения, приложим к нему известный момент в сечении левее точки 2, равный 6, растягивающий верхние волокна, что следует из рис. 49,б, и вращающий узел против часовой стрелки, и внешний момент 10. Искомый момент M_2Н в сечении ниже точки 2 в этом случае равен 10−6=4, вращает узел против часовой стрелки (рис. 49,в). Обратим внимание на тот факт, что полученный из равновесия узла 2 момент, равный 4, растягивает левые волокна на стойке 2−4.

На следующем стандартном шаге ликвидируем условную заделку левее сечения 2 и переставим ее в сечение выше точки 4 (рис49,г). При этом в сечении 2 восстанавливаются ее кинематические характеристики. Далее рассмотрим участок 2−4. Приложим к нему сосредоточенный момент М=4, полученный из равновесия узла 2 и растягивающий левые волокна. Это аналог случая 2 на рис. 21, а эпюра на этом участке показана на рис. 50,а. На участке 3−4 эпюра аналогична первому частному случаю (рис.18), а величина момента, растягивающего верхние волокна в сечении правее точки 4 равна М_4П=5Ч2=10 (рис. 50,б).

Для перехода на участок 4−5 необходимо «уравновесить» узел 4, т. е. добиться, чтобы сумма моментов относительно оси узла 4 была бы равна нулю. Для этого «вырежем» узел 4 с помощью замкнутого сечения, приложим к нему известные моменты в сечениях правее и выше точки 4, равные, соответственно, 10 и 4. Оба они вращают вырезанный узел по часовой стрелке. Искомый момент M_4Л в сечении левее точки 4 в этом случае равен 4+10=14, вращает узел против часовой стрелки (рис. 50,в). Обратим внимание на тот факт, что полученный из равновесия узла 4 момент, равный 14, растягивает верхние волокна.

Далее рассмотрим участок 4−5. Приложим к нему сосредоточенный момент М=14, полученный из равновесия узла 4 и растягивающий верхние волокна, в точке 4 приложим также сосредоточенные силы Р₁=3 и Р₂=5, перенесенные с участков 1−2 и 4−3, параллельных расчетному и рассмотренных ранее и равномерно-распределенную нагрузку q=3. Исходя из принципа независимости действия сил, вычислим величину изгибающего момента в сечении 5. Независимое действие сосредоточенного момента М=14 соответствует частному случаю 2 (стр.21), приводя к растяжению верхних волокон. Отложим ординату выше нейтральной оси (рис. 50,г). Воздействие равномерно-распределенной нагрузки на участок 4−5 приводит к возникновению изгибающего момента, растягивающего нижние волокна (по третьему частному случаю) и равного М=qЧL²/2=3Ч4²/2=24. Суммарное воздействие двух сосредоточенных сил приводит к растяжению верхних волокон, а вызванный ими изгибающий.

момент равен (3+5)Ч4=60. Алгебраическая сумма воздействий (в данном случае изгибающих моментов) в заделке 5 равна М₅=74−24=50. Этот момент растягивает верхние волокна. В пределах характерного участка 4−5 эпюра изгибающих моментов должна быть очерчена по квадратной параболе с выпуклостью вверх. Результат проведенного расчета на участке 4−5 (без уточнения поведения эпюры на этом участке) — на рис. 51,а. На рис. 51,б показан процесс построения эпюры Q на участке 4−5. На участке 4−5 на эпюре Q происходит изменение знака, что указывает на наличие экстремума на эпюре М. На рис. 51,в приведены полные эпюры изгибающих моментов и поперечных сил для рассматриваемой задачи.

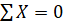
Построение эпюры продольных сил начнем, вырезав узел 2 с эпюры Q. На рис. 52, а показан узел 2 с приложенными к его стержням положительно направленными искомыми продольными силами N₂₋₁ и N₂₋₄, известными и направленными в соответствии со знаками поперечными силами левее и ниже этого узла. Из уравнений равновесия получены величины и знаки искомых продольных сил. Далее вырезаем узел 3. При этом обратим внимание на тот факт, что на участке 3−4 в сечении 3 отсутствует продольная нагрузка, что указывает со всей очевидностью на отсутствие на этом участке продольной силы. На рис. 52,б рассматривается узел 4 с приложенной искомой продольной силой N₄₋₅, известной сжимающей продольной силой N₂₋₄=3, направленной «к узлу», поперечными силами левее, правее и выше этого узла. Из уравнения равновесия получены величина искомой продольной силы. На рис. 52,в можно ознакомиться с эпюрой продольных сил для рассмотренного примера.

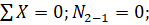
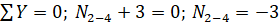
Построение эпюр внутренних усилий в трехшарнирных рамах.