Задачи теории упругости

Колебания упругой среды (в перемещениях) описываются уравнениями Ляме:

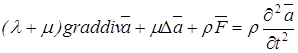
(1.1).

где л, м — константы Ляме, положительность которых обеспечивает обратимость закона Гука, с — плотность среды.

• (x₁, x₂, x₃, t)=(u (x₁, x₂, x₃, t), v (x₁, x₂, x₃, t), w (x₁, x₂, x₃, t))^T
• — вектор перемещений.

Рассматриваемая упругая среда может быть пространством, полупространством (в том числе стратифицированным), слоем или пакетом слоев.

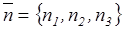
Механическое состояние упругого тела, занимающего в начальном состоянии известный объем V с ограничивающей поверхностью S, характеризуется компонентами тензора деформации е_ij и тензора напряжений у_ij. Перемещения в точках тела, под действием заданной системы поверхностных и объемных сил, описываются вектором перемещений и представляют собой непрерывные и однозначные функции координат и времени. Механическое состояние упругого тела характеризуется также вектором напряжений ф, возникающих в упругом теле на некоторой элементарной площадке с нормалью. Вектор ф выражается через компоненты тензора напряжений.

.

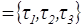
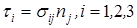
Вектор напряжений ф можно выразить через перемещения:

=T,.

где Т — линейный дифференциальный оператор напряжений. В изотропном случае:

.

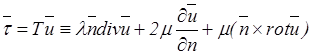
В случае установившихся колебаний зависимость всех характеристик задачи от времени t описывается множителем, а уравнения линейной упругости, описывающие установившийся закон колебаний, имеют вид:

(1.2).

Для постановки задач теории упругости должны быть заданы, индивидуальные для конкретных задач, граничные условия, а в случае динамических задач — еще и начальные условия.

Интегральное представление решения задачи строится на основе интегральных соотношений между напряжениями и перемещениями, существующих для упругих сред. При этом используется формула Бетти в виде:

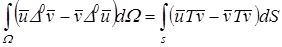
(1.3).

.

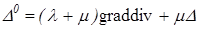
В этом соотношении вектор-функции u, v-произвольные дважды непрерывно дифференцируемые. Область может быть неограниченной с гладкой границей.

Вводится система следующих векторов:

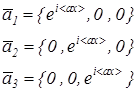
(1.4).

.

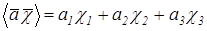
Эти векторы формируют матрицу:

(1.5).

В соотношении (1.2) вместо произвольного вектора u вносится решение дифференциального уравнения:

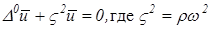
(1.6).

а вместо вектора v — матрицу V. Тогда соотношение (1.2) порождает не скалярное, а векторное выражение.

Выражение имеет вид:

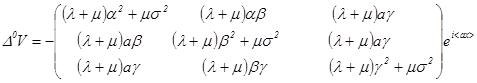
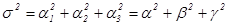
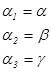
(1.7).

Матрицу справа обозначим как В, тогда векторы — формируемые строками этой матрицы. Можно записать:

Вычисляются векторы. В результате вычислений будут получены формулы:

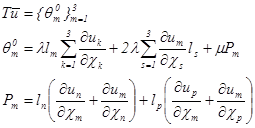
(1.9).

здесь для m=1, 2, 3 берется соответственно по порядку n=2, p=3; n=1, p=3; n=1, p=2;

.

Внося в эти соотношения вместо u значения векторов, получаем:

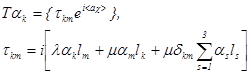
(1.10).

Вектор напряжений, действующих на границе S, будем обозначать.

(1.11).

где T_k — проекции вектора напряжений на направления осей x_k соответственно.

Вычисляя вектор Tu на границе S с учетом (1.9) и соотношения:

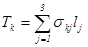
получаем выражение для вектора Tu:

Tu=T₀ (1.12).

Внося соотношения (1.9), (1.10), (1.12), в (1.2) для каждого вектора, и вектора решения уравнения (1.2) приходим к соотношению:

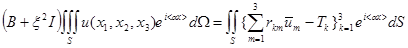
(1.13).

где I-единичная матрица третьего порядка.

Если разрешить соотношения (1.13) относительно тройного интеграла в левой части, то получим преобразование Фурье искомого решения краевой задачи для дифференциального уравнения (1.6). Оно будет зависеть как от значения вектора перемещений на границе области, так и от вектора напряжений. Так как в любой области на границе S может быть задан согласно постановке задачи теории упругости лишь один из этих векторов, то между компонентами вектора перемещений и напряжений на границе должны существовать определенные зависимости.