Уравнение линейной регрессии

Задача 1.

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (X, млн. руб.).

Требуется: капиталовложение график экономический Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков; построить график остатков.

Проверить выполнение предпосылок МНК.

Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента.

Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью критерия Фишера, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

Осуществить прогнозирование среднего значения показателя Y при уровне значимости, если прогнозное значения фактора Х составит 80% от его максимального значения.

Представить графически: фактические и модельные значения Y точки прогноза.

Составить уравнения нелинейной регрессии:

• · гиперболической;
• · степенной;
• · показательной.

Привести графики построенных уравнений регрессии.

Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

Таблица 1.

Решение:

Построим линейную модель .

Для удобства выполнения расчетов предварительно упорядочим всю таблицу исходных данных по возрастанию факторной переменной Х (Данные > Сортировка). Рис 1.

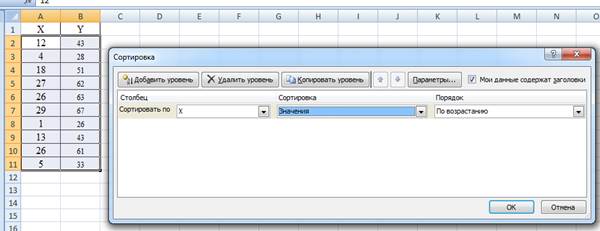
Рис 1.Сортировка

Используем программу РЕГРЕССИЯ и найдем коэффициенты модели: Рис 2.

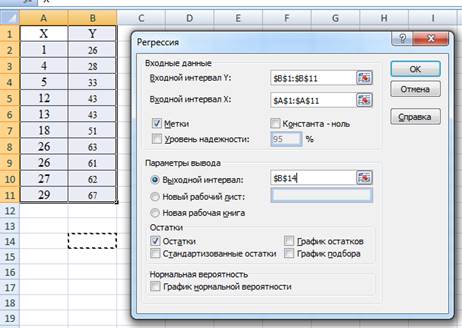
Рис 2.Регрессия

Результаты вычислений представлены в таблицах 2 — 5.

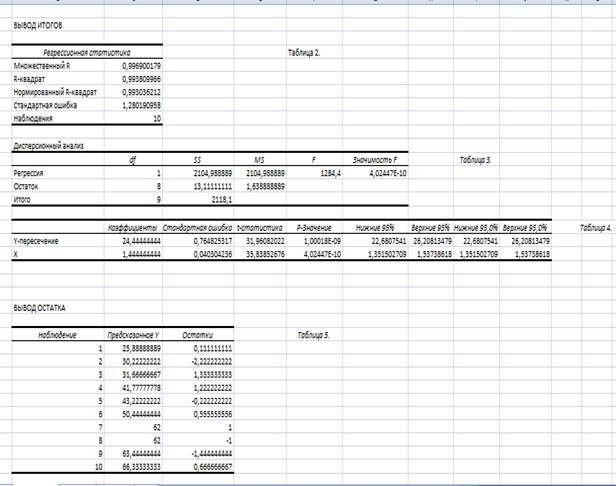
Коэффициенты модели содержатся в таблице 4 (столбец Коэффициенты).

Таким образом, модель построена, и ее уравнение имеет вид.

Коэффициент регрессии b=1,44 следовательно, при увеличении объема капиталовложений (X, млн. руб.) на 1 млн. руб объем выпуска продукции (Y млн. руб.) увеличится в среднем на 1,44 млн руб.

Свободный член a=24,44 в данном уравнении не имеет реального смысла.

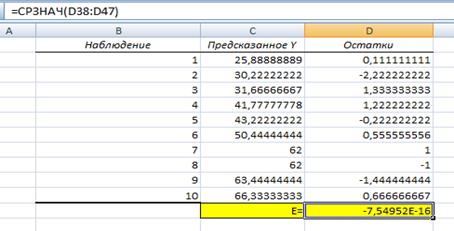
2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков; построить график остатков Остатки модели содержатся в столбце Остатки итогов программы РЕГРЕССИЯ (таблица 5).

Программой РЕГРЕССИЯ найдены также остаточная сумма квадратов и дисперсия остатков (таблица 3).

Для построения графика остатков нужно выполнить следующие действия:

• 1) Вызвать Мастер диаграмм, выбрать тип диаграммы Точечная (с соединенными точками).
• 2) Для указания данных для построения диаграммы зайти во вкладку Ряд, нажать кнопку Добавить; в качестве значений Х указать исходные данные Х (таблица 1); значения У — остатки (таблица 5).Рис 3.

Рис 3. Построение графика остатков.

В результате получим график остатков: Рис4.

Рис4.График остатков.

3. Проверить выполнение предпосылок МНК Предпосылками построения классической линейной регрессионной модели являются четыре условия, известные как условия Гаусса-Маркова.

• 1) В уравнении линейной модели слагаемое е — случайная величина, которая выражает случайный характер результирующей переменной Y.
• 2) Математическое ожидание случайного члена в любом наблюдении равно нулю, а дисперсия постоянна.
• 3) Случайные члены для любых двух разных наблюдений независимы (некоррелированы).
• 4) Распределение случайного члена является нормальным.
• 1) Проведем проверку случайности остаточной компоненты по критерию поворотных точек.

Количество поворотных точек определим по графику остатков: .

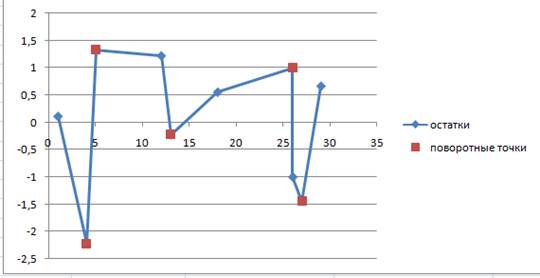
Рис 5.Поворотные точки.

Вычислим критическое значение по формуле.

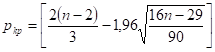
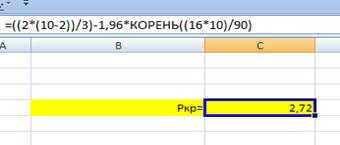
При найдем Схема критерия:

Сравним, следовательно, свойство случайности для ряда остатков выполняется.

2) Равенство нулю математического ожидания остаточной компоненты для линейной модели, коэффициенты которой определены по методу наименьших квадратов, выполняется автоматически.

С помощью функции СРЗНАЧ для ряда остатков можно проверить: .

Свойство постоянства дисперсии остаточной компоненты проверим по критерию Голдфельда-Квандта.

В упорядоченных по возрастанию переменной Х исходных данных () выделим первые 4 и последние 4 уровня средние 2 уровня не рассматриваем С помощью программы РЕГРЕССИЯ построим модель по первым четырем наблюдениям (регрессия-1), для этой модели остаточная сумма квадратов .

С помощью программы РЕГРЕССИЯ построим модель по последним четырем наблюдениям (регрессия-2), для этой модели остаточная сумма квадратов .

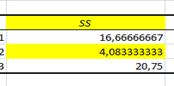
Рассчитаем статистику критерия:

.

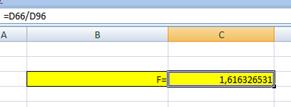
Критическое значение при уровне значимости и числах степеней свободы составляет (функция FРАСПОБР).

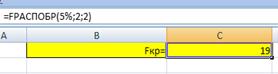
Схема критерия:

Сравним, следовательно, свойство постоянства дисперсии остатков выполняется, модель гомоскедастичая.

3)Для проверки независимости уровней ряда остатков используем критерий Дарбина-Уотсона.

.

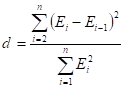
Предварительно по столбцу остатков с помощью функции СУММКВРАЗН определим; для этого остатки со второго до последнего отнимем остатки с первого до предпоследнего.

используем найденную программой РЕГРЕССИЯ сумму квадратов остаточной компоненты .

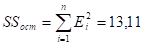
Таким образом, .

Схема критерия:

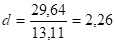
Полученное значение, что свидетельствует об отрицательной корреляции. критические уровни и, которые определяются по таблице d-статистик при n=10 Дарбина-Уотсона .

Сравним: d=2,26?(2;4) значит нужно перейти к d'=4-d=1,74 лежит в интервале от до 2, следовательно, свойство независимости остаточной компоненты выполняется.

Проверим выполнение свойства независимости ряда остатков по первому коэффициенту автокорреляции.

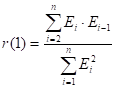
С помощью функции СУММПРОИЗВ найдем для остатков ,.

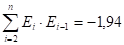
следовательно, .

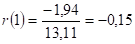
Критическое значение для коэффициента автокорреляции определяется как отношение и составляет для данной задачи .

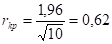
Схема критерия:

Сравнение показывает, что, следовательно, ряд остатков некоррелирован.

4) Соответствие ряда остатков нормальному закону распределения проверим с помощью R/S — критерия.

.

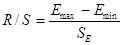
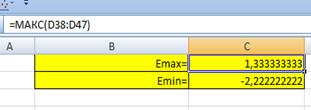
С помощью функций МАКС и МИН для ряда остатков определим, .

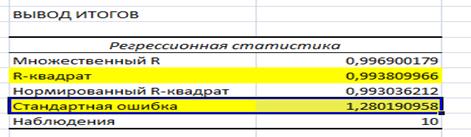
Стандартная ошибка модели найдена программой РЕГРЕССИЯ и составляет (таблица 2).

Тогда.

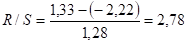
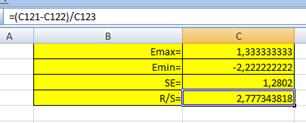
Критический интервал определяется по таблице критических границ отношенияR/S и при составляет .

Схема критерия:

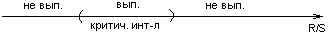
значит, для построенной модели свойство нормального распределения остаточной компоненты выполняется.

Проведенная проверка предпосылок регрессионного анализа показала, что для модели выполняются все условия Гаусса-Маркова.

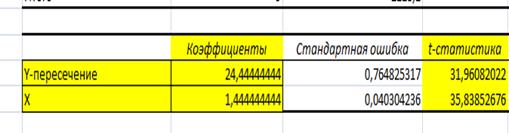
4. Осуществить проверку значимости параметров уравнения регрессии с помощьюt — критерия Стьюдента ().

tстатистики для коэффициентов уравнения регрессии приведены в таблице 4.

Для свободного коэффициента определена статистика .

Для коэффициента регрессии определена статистика .

Критическое значение найдено для уровня значимости =5% и числа степеней свободы (функция СТЬЮДРАСПОБР).

Схема критерия:

Сравнение показывает:

>, следовательно, свободный коэффициент, а является значимым, его и фактор объем выпуска продукции нужно сохранить в модели.

>, значит, коэффициент регрессии b является значимым, его и фактор объем капиталовложений нужно сохранить в модели.

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F — критерия Фишера (), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

Коэффициент детерминации R-квадрат определен программой РЕГРЕССИЯ (таблица 2) и составляет R2 = 0,994 = 99,4% .

Таким образом, вариация (изменение) объема выпуска продукции Y на 99,4% объясняется по полученному уравнению вариацией объема капиталовложений Х.

Проверим значимость полученного уравнения с помощью F — критерия Фишера.

F — статистика определена программой РЕГРЕССИЯ (таблица 3) и составляет .

Критическое значение Fкр= 5,32найдено для уровня значимости =5% и чисел степеней свободы k1=1, k2=8 (функция FРАСПОБР).

Схема критерия:

Сравнение показывает: F = 1284,4>Fкр = 5,31; следовательно, уравнение модели является значимым, его использование целесообразно, зависимая переменная У достаточно хорошо описывается включенной в модель факторной переменной Х.

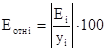
Для вычисления средней относительной ошибки аппроксимации дополним таблицу 5 столбцом относительных погрешностей, которые вычислим по формуле с помощью функции ABS (таблица 6).

По столбцу относительных погрешностей найдем среднее значение (функция СРЗНАЧ).

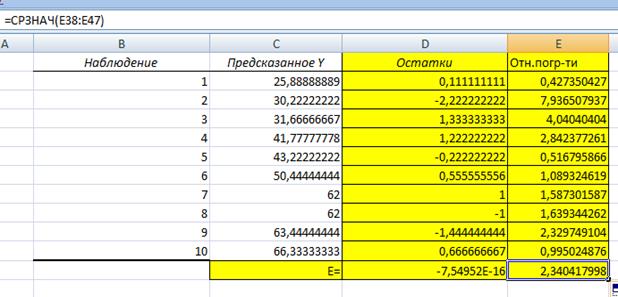
Схема проверки:

Сравним:, следовательно, модель точная.

Вывод: на основании проверки предпосылок МНК, критериев Стьюдента и Фишера и величины коэффициента детерминации модель можно считать адекватной, и такую модель можно использовать для анализа и прогнозирования .

6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости, если прогнозное значения фактора Х составит 80% от его максимального значения.

Прогнозное значение факторной переменной Х составит .

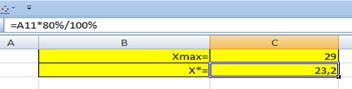
Рассчитаем по уравнению модели прогнозное значение показателя У:

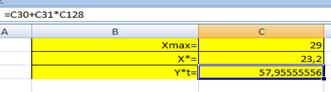
Таким образом, если объем капиталовложений составит 23,2 млн. руб, то ожидаемый объем выпуска продукции будет около 57,96 млн руб.

Зададим доверительную вероятность и построим доверительный прогнозный интервал для среднего значения Y.

Для этого нужно рассчитать стандартную ошибку прогнозирования.

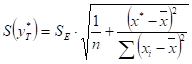
Предварительно подготовим:

— стандартную ошибку модели SE=1,28 (Таблица 2);

— по столбцу исходных данных Х найдем среднее значение (функция СРЗНАЧ) и определим (функция КВАДРОТКЛ).

Следовательно, стандартная ошибка прогнозирования для среднего значения составляет:

.

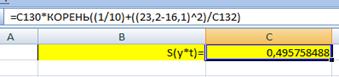
При размах доверительного интервала для среднего значения.

.

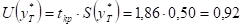
Границами прогнозного интервала будут.

;

.

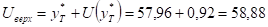
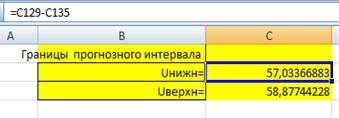
Таким образом, с надежностью 90% можно утверждать, что если объем капиталовложений составит 23,2 млн. руб, то ожидаемый средний объем выпуска продукции будет от 57,03 млн руб. до 58,88 млн руб.

Прогнозный интервал узок вследствие точности построенной модели.

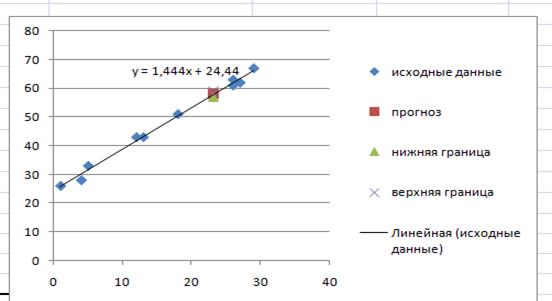
7. Представить графически: фактические и модельные значения У, результаты прогнозирования.

Для построения чертежа используем Мастер диаграмм (точечная) — покажем исходные данные (поле корреляции).

Затем с помощью опции Добавить линию тренда… построим линию модели:

тип > линейная; параметры > показывать уравнение на диаграмме.

Покажем на графике результаты прогнозирования. Для этого в опции Исходные данные добавим ряды:

Имя > прогноз; значения Х > х*; значения У > у*;

Имя > нижняя граница; значения Х > х*; значения У > Uнижн;

Имя > верхняя граница; значения Х > х*; значения У > Uверх.

8. Составить уравнения нелинейной регрессии:

• · гиперболической;
• · степенной;
• · показательной.

Привести графики построенных уравнений регрессии.

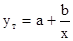
Гиперболическая модель не является стандартной.

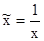
Для ее построения выполним линеаризацию: обозначим и получим вспомогательную модель Вспомогательная модель является линейной. Ее можно построить с помощью программы РЕГРЕССИЯ, предварительно подготовив исходные данные: столбец значений уi (остается без изменений) и столбец преобразованных значений (таблица 7).

С помощью программы РЕГРЕССИЯ получим:

Таким образом,, следовательно, уравнение гиперболической модели .

С помощью полученного уравнения рассчитаем теоретические значения для каждого уровня исходных данных .

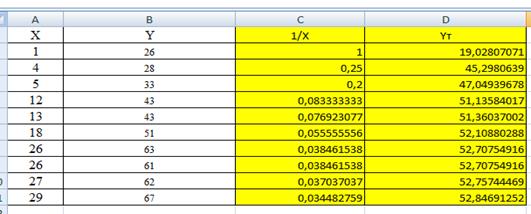
Покажем линию гиперболической модели на графике. Для этого добавим к ряду исходных данных ряд теоретических значений .

Степенная модель является стандартной. Для ее построения используем Мастер диаграмм: исходные данные покажем с помощью точечной диаграммы, затем добавим линию степенного тренда и выведем на диаграмму уравнение модели.

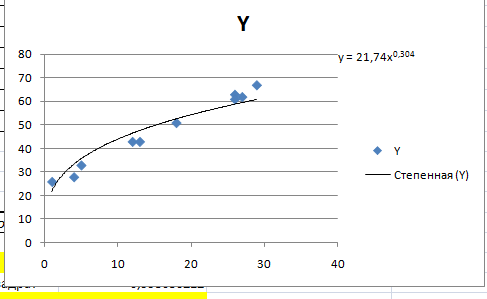
Таким образом, уравнение степенной модели .

Показательная модель тоже стандартная (экспоненциальная).

Построим ее с помощью Мастера диаграмм.

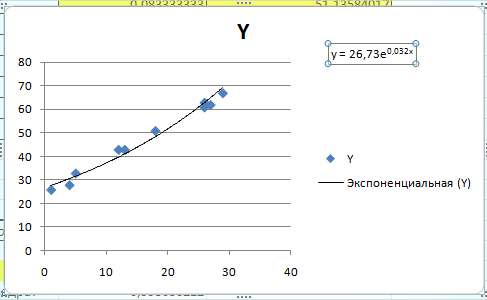
Таким образом, уравнение показательной модели y=26,73.

Можно вычислить (функция ЕХР), тогда уравнение показательной модели .

9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

Заполним для каждой модели расчетную таблицу, в которую занесем теоретические значения, найденные по соответствующему уравнению для каждого уровня исходных данных; ошибки модели и относительные погрешности (таблицы 8−10).

Среднюю относительную погрешность найдем по столбцу с помощью функции СРЗНАЧ.

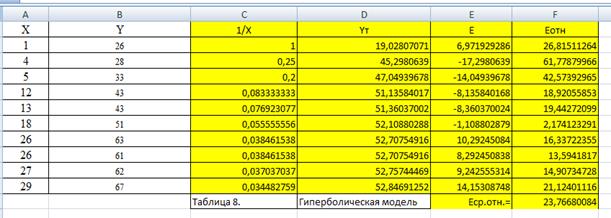
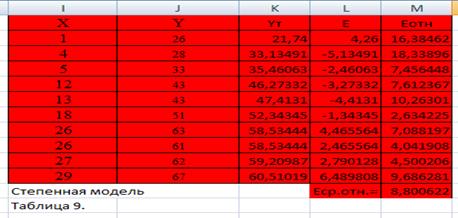
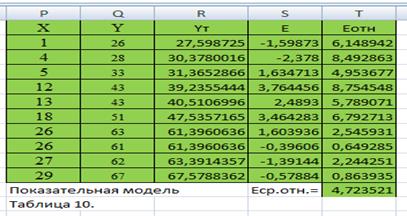
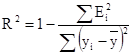
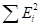
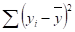
Индекс детерминации вычислим по формуле, для чего подготовим числитель дроби — функция СУММКВ для столбца ошибок и знаменатель — функция КВАДРОТКЛ для столбца У.

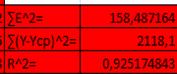
Составим сводную таблицу характеристик качества построенных моделей:

Столбец средних относительных погрешностей показывает, что наиболее точной является степенная модель, ее погрешность — наименьшая., следовательно, точность степенной модели точная.

По величине индекса детерминации лучшая модель — линейная (индекс детерминации наибольший)., таким образом, вариация (изменение) объема выпуска продукции на 99,3% объясняется по уравнению линейной модели вариацией объема капиталовложений .

Для нелинейных моделей коэффициенты эластичности определяются соотношением, согласно которому:

для степенной модели коэффициент эластичности и представляет собой постоянную величину;

для показательной модели коэффициент эластичности и зависит от значения фактора Х;

для гиперболической модели коэффициент эластичности и также зависит от значения фактора Х.

Для построенной степенной модели получим. Следовательно, согласно этой модели увеличение объема капиталовложений на 1% приводит к увеличению среднего объема выпуска продукции на 0,30%.

Для показательной и гиперболической моделей результаты расчета коэффициентов эластичности приведены в таблице.

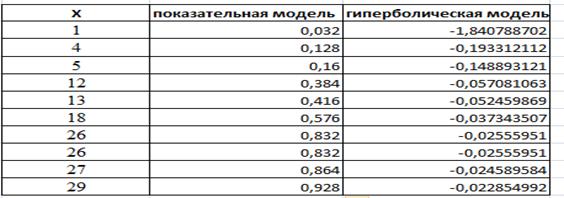
Вывод: Таким образом, согласно показательной модели увеличение объема капиталовложений на 1% приводит к росту среднего объема выпуска продукции на величину от 0,032% до 0,928%. Согласно гиперболической модели при увеличении объема капиталовложений на 1% происходит увеличение среднего объема выпуска продукции в пределах от -1,84% до -0,02%.

Окончательный вывод о качестве моделей по коэффициентам эластичности следует делать с учетом экономического смысла задачи.

Логично предположить, что наиболее подходящей является показательная модель, т.к. наблюдаемый рост коэффициента эластичности соответствует реальной ситуации: чем больше объем капиталовложений, тем сильнее это сказывается на объеме выпуска продукции .

Задача 2.

Приведены временные ряды Y (t) социально-экономических показателей по Алтайскому краю за период с 2000 г. по 2011 г. Требуется исследовать динамику показателя.

Задание:

• 1. Проверить наличие аномальных наблюдений, используя метод Ирвина (б=5%).
• 2. Построить линейную модель временного ряда yt=a+b•t, параметры которой оценить МНК.
• 3. Оценить адекватность построенной модели, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения.
• 4. Оценить качество модели, используя среднюю относительную погрешность аппроксимации.
• 5. Осуществить прогноз на следующий год (прогнозный интревал рассчитать при доверительной вероятности 70%).
• 6. Представить графически фактические значения показателя, результаты моделирования и прогнозирования.

Решение:

1 Проверить наличие аномальных наблюдений, используя метод Ирвина (б=5%).

Подготовим Sy=21 913,87(СТАНДОТКЛОН) и рассчитаем статистики:

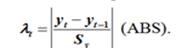
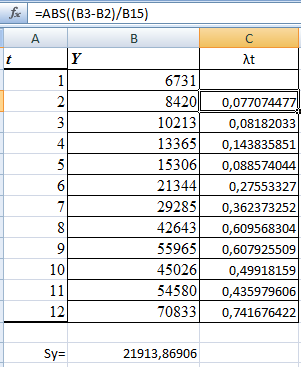
Критическое значение при n=12 и уровне значимости (б=5%) составляет лкр=1,5.

Сравним лt=0,74<�лкр=1,5 значит аномальных наблюдений нет.

2. Построить линейную модель временного ряда yt=a+b•t, параметры которой оценить МНК.

С помощью программы «РЕГРЕССИЯ» найдем:

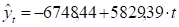
Таким образом,;. Модель построена, ее уравнение имеет вид .

Коэффициент регрессии показывает, что с каждым годом социально-экономические показатели по Алтайскому краю увеличиваются в среднем на 5829,39 .

3. Оценить адекватность построенной модели, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения.

Проверка перечисленных свойств состоит в исследовании Ряда остатков, который содержится в таблице «Вывод остатка» итогов РЕГРЕССИИ.

Для проверки свойства случайности остаточной компоненты используем критерий поворотных точек (пиков), основой которого является определение количества поворотных точек для ряда остатков.

С помощью Мастера диаграмм построим график остатков.

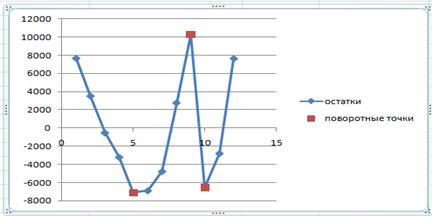
Поворотными считаются точки максимумов и минимумов на этом графике (в данном случае — первая, пятая, девятая, десятая, и двенадцатая). Их количество .

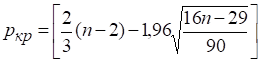
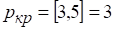
По формуле при вычислим критическое значение .

Сравним значения p и pкр и сделаем вывод согласно схеме:

=, следовательно, свойство случайности для ряда остатков не выполняется.

Для проверки свойства независимости остаточной компоненты используем критерий Дарбина-Уотсона.

Согласно этому критерию вычислим по формуле статистику.

.

Подготовим для вычислений: ,.

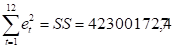
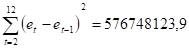
(функция СУММКВРАЗН).

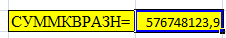
Таким образом, .

По таблице d — статистик Дарбина — Уотсона определим критические уровни: нижний d1 = 0,97 и верхний d2 = 1,33.

Сравним полученную фактическую величину d с критическими уровнями d1 и d2 и сделаем вывод согласно схеме:

следовательно, свойство независимости остатков для построенной модели выполняется.

Для проверки соответствия ряда остатков нормальному закону распределения используется R/S критерий.

В соответствии с этим критерием вычислим по формуле статистику.

.

Подготовим для вычислений:

— максимальный уровень ряда остатков (функция МАКС);

— минимальный уровень ряда остатков (функция МИН);

— стандартная ошибка модели (таблица «Регрессионная статистика» вывода итогов РЕГРЕССИИ).

Получим .

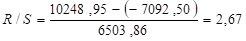
По таблице критических границ отношения R/S определим критический интервал. При n= 12 можно использовать .

Сопоставим фактическую величину R/S с критическим интервалом и сделаем вывод согласно схеме:

значит, для построенной модели свойство нормального распределения остаточной компоненты не выполняется.

Проведенная проверка показывает, что для построенной модели не все свойства выполняются. Таким образом, данная трендовая модель не является адекватной реальному ряду наблюдений, её нельзя использовать для построения прогнозных оценок.

4. Оценить качество модели, используя среднюю относительную погрешность аппроксимации.

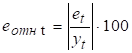
Используем исходные данные и найденные программой РЕГРЕССИЯ остатки (таблица «Вывод остатка»). По формуле рассчитаем столбец относительных погрешностей и найдем среднее значение .

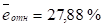
Сравнение показывает, что. Следовательно, точность модели не удовлетворительная.

5. Осуществить прогноз на следующий год (прогнозный интревал рассчитать при доверительной вероятности 70%).

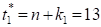
«Следующие год» соответствует периоду упреждения и, при этом и.

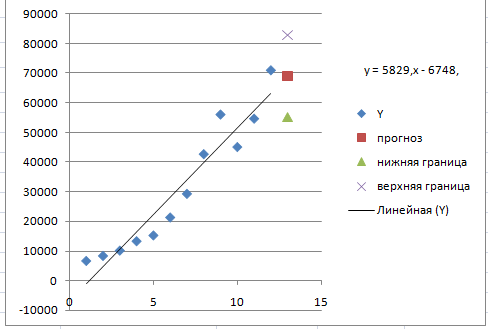
Согласно уравнению модели получим точечные прогнозные оценки Таким образом, ожидаемые социально-экономические показатели на следующий год будут составлять около 69 033,63 .

Для оценки точности прогнозирования рассчитаем границы прогнозных интервалов для индивидуальных значений результирующего признака (доверительная вероятность).

Подготовим: (функция СТЬЮДРАСПОБР при);

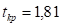
(строка «стандартная ошибка» итогов РЕГРЕССИИ);

(функция СРЗНАЧ); (функция КВАДРОТКЛ).

Вычислим размах прогнозного интервала для индивидуальных значений, используя формулу.

.

При получим и определим границы доверительного интервала:; .

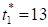
Таким образом, с надежностью 70% можно утверждать, что социально-экономические показатели в Алтайском крае в следующем (13-ом) году будут составлять от 55 191,94 до 82 875,28 .

6. Представить графически фактические значения показателя, результаты моделирования и прогнозирования Для построения чертежа используем Мастер диаграмм (точечная) — покажем исходные данные.

Затем с помощью опции Добавить линию тренда… построим линию модели:

тип > линейная; параметры > показывать уравнение на диаграмме.

Покажем на графике результаты прогнозирования. Для этого в опции Исходные данные добавим ряды:

Имя > прогноз; значения Х > и; значения Y > ;

Имя > нижние границы; значения Х > и; значения Y > ;

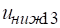
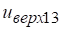
Имя > верхние границы; значения Х > и; значения Y > .

Результаты прогнозирования и моделирования.