Описание используемых алгоритмов

Извлечение 2D ортографической информации

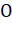
Каркасная модель объекта строится по фронтальной проекции (FV — front view), боковой проекции — виду справа (SV — side view) и верхней проекции — вид сверху (TV — top view), которые подаются на вход программе в формате систем автоматизированного проектирования (САПР) DXF. Файл каждой проекции необходимо проанализировать и загрузить информацию о хранящихся в нем геометрических компонентах — вершинах и ребрах — в матрицы :

.

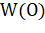
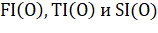
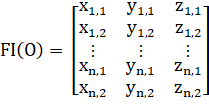
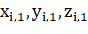
где — координаты вершины — начала ребра,.

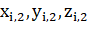
— координаты вершины — конца ребра,.

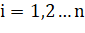
где ,.

n — количество ребер в проекции.

Каждое ребро задается координатами двух вершин, координаты одной вершины могут встречаться в описании несколько раз по количеству сходящих в ней ребер.

Разметка 2D граней и вершин

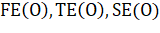
Для того чтобы уменьшить количество параметров, определяющих ребра, каждая вершина отмечается порядковым номером. Номера вершин будут описывать ребра вместо координат этих вершин. Кроме того, сами ребра также отмечаются порядковыми номерами. Таким образом для каждой проекции создаются матрицы и для хранения информации о вершинах и ребрах соответственно:

.

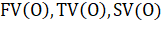
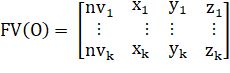
где — порядковый номер i-ой вершины,.

— координаты i-ой вершины, i =1,2,…, k.

k — количество вершин проекции.

.

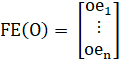
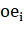
где — объект типа «ребро», i = 1,2,…, n.

n — количество ребер проекции.

Каждый объект типа «ребро» содержит4 следующую информацию:

.

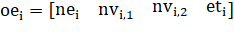
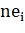
где — порядковый номер ребра,.

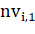
— порядковый номер вершины, определяющей начало ребра,.

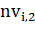
— порядковый номер вершины, определяющей конец ребра,.

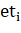
— тип ребра,.

i = 1,2,…, n,.

n — количество ребер проекции.

Таким образом, матрица вершин содержит порядковые номера вершин проекции и их координаты, а матрица ребер — порядковые номера ребер и порядковые номера вершин, определяющих эти ребра. Тип ребер предлагается запоминать для обработки пунктирных линий на проекции, которые обычно используются для обозначения ребер, находящихся не на лицевых гранях проекции.

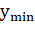
Координаты вершин проекций могут значительно отличаться, поэтому для упрощения работы с ними предлагается сдвинуть каждую проекцию таким образом, чтобы она находилась в первом квадранте и хотя бы одна точка лежала на оси X и хотя бы одна точка лежала на оси Y. Для этого необходимо найти минимальную координату и минимальную координату вершин в каждой проекции. После этого необходимо выполнить следующую операцию для матриц каждой проекции:

.

.

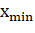
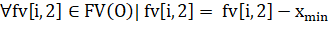
где fv[i, 2] - элемент i-ой строки и второго столбца матрицы ,.

fv[i, 3] - элемент i-ой строки и третьего столбца матрицы .

Впоследствии ребра проекции будут сравниваться с ребрами каркасной модели. Так как одно ребро проекции может описывать большое количество ребер в каркасной модели, ребра проекции должны быть максимальной длины, а не множеством коротких отрезков, лежащих на одной прямой.

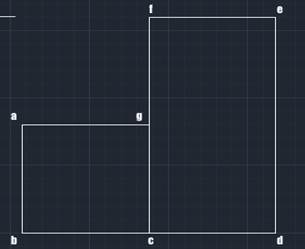
Рисунок 3 Вид сбоку.

Например, на рисунке 3 представлена проекция некоторого объекта. В конечной матрице проекции не должно существовать несколько ребер, лежащих на одной прямой и пересекающихся в вершинах, таких как bc, cd и fg, gc. Если они были обнаружены, то оба ребра, лежащие на одной прямой, удаляются из, и добавляются ребра bd и fc соответственно.