Введение. 
Линейное программирование. 
Методы нелинейной оптимизации

Предлагаемый к изучению предмет является частью прикладной математики. Структуру изучаемой и смежных областей знаний можно представить в виде следующей схемы.

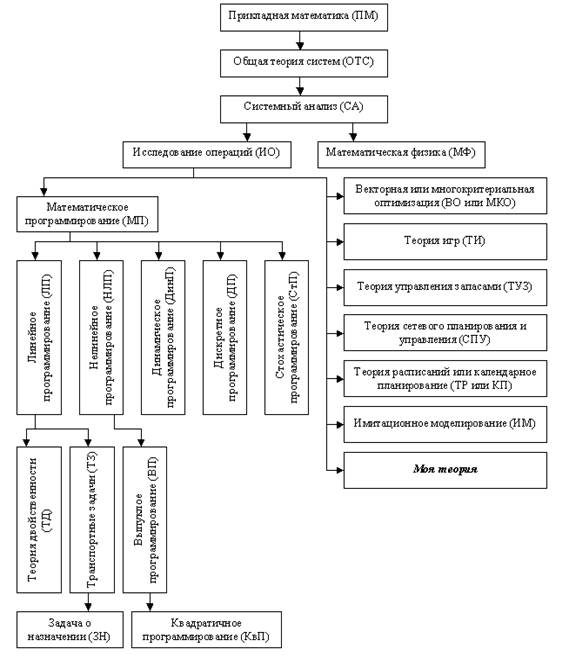
Общая теория систем сформировалась в последние десятилетия двадцатого века как дисциплина, изучающая общие свойства сложных систем различной природы.

Системный анализ — методология анализа сложных систем различной природы (экономических, технических, биологических, социальных). Он предполагает структуризацию системы, формулировку целей и анализ полученных подсистем с помощью математических методов.

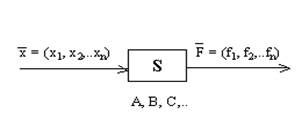
Система — совокупность взаимосвязанных элементов. Она описывается некоторыми параметрами, среди которых выделяют исходные (), управляемые (A, B, C…) и выходные (). Задача анализа системы ставится как задача принятия решений, то есть задача выбора таких управляемых параметров, которые обеспечивают наилучшие показатели деятельности системы. Цели функционирования системы могут быть разные и обычно формулируются постановщиком задачи, лицом, принимающим решения.

Исследование операций занимается изучением количественных методов анализа результатов целенаправленной человеческой деятельности с помощью экономико-математических методов.

Системы, не являющиеся результатом человеческой деятельности, изучаются в рамках общей теории систем другими специализированными дисциплинами. Примером такой дисциплины является математическая физика. линейный программирование оптимизация симплекс.

Математическая физика — наука, которая изучает поведение сплошных сред. К математической физике, в частности, относится механика жидкости, газа и твердых тел.

Задачи принятия решений Исследование операций включает в себя целый ряд научных дисциплин, отличающихся целями и методами принимаемых решений:

· Математическое программирование изучает такие задачи принятия решений, в которых наилучшим решением является такое, на котором достигается наибольшее (или наименьшее) значение некоторого показателя эффективности:

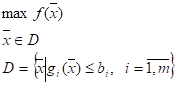
где.

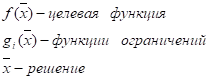
Задача относится к классу экстремальных задач. Если область допустимых решений D совпадает с пространством вещественных чисел R, то есть отсутствуют ограничения, то данная экстремальная задача является классической задачей оптимизации.

• · Линейное программирование. Задача линейного программирования — это задача математического программирования, в которой целевая функция и функции ограничений линейные. Для таких задач разработаны точные методы решений.
• · Транспортные задачи — задачи линейного программирования специального вида, имеющие более эффективные методы решений.
• · Задачи о назначениях — задачи о распределении работы между исполнителями с целью достижения максимальной эффективности.
• · Задачи нелинейного программирования — задачи математического программирования, в которых хотя бы одна из функций нелинейна. В общем случае эти задачи не имеют точных аналитических методов решений. Основные методы их решения — приближенные.
• · Задачи выпуклого программирования — задачи нелинейного программирования, имеющие вогнутую () функцию цели и выпуклую () область допустимых значений. Это гарантирует одноэкстремальность задачи и позволяет сформулировать признак оптимальности решения.
• · Задачи квадратичного программирования — задачи выпуклого программирования, имеющие квадратичную целевую функцию с линейными ограничениями.
• · Задачи дискретного программирования — задачи математического программирования, имеющие дискретную область допустимых решений (в частности, конечное или счетное множество решений).
• · Задачи динамического программирования — задачи, в которых применяются пошаговые методы решения.
• · Задачи стохастического программирования — задачи, в которых используются функции случайных величин.
• · Векторная (многокритериальная) оптимизация изучает задачи исследования операций, в которых требуется обеспечить наибольшее (наименьшее) значение нескольким показателям эффективности в одной и той же области допустимых решений.
• ·

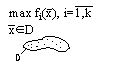
• · Теория игр рассматривает задачи принятия решений в конфликтных ситуациях.
• · Теория управления запасами изучает задачи определения объемов поставки и сроков хранения продукции.
• · Сетевое планирование и управление предлагает методы планирования работ, связанных сетевыми графиками.
• · Теория расписаний или теория календарного планирования рассматривает методы планирования работ во времени.
• · Имитационное моделирование — моделирование систем с помощью электронной вычислительной техники.
• · Моя теория — это Ваша, читатель, теория, которую Вы разработаете для решения прикладных задач, которые встанут перед Вами в ходе Вашей профессиональной деятельности. Для этого Вам потребуется использовать уже известные методы принятия решений, в первую очередь это методы решения экстремальных задач.

Математическое моделирование.

Моделирование — замена одного объекта другим с целью изучения их общих свойств.

По средствам моделирования методы моделирования можно разбить на две группы: методы материального моделирования и методы идеального моделирования.

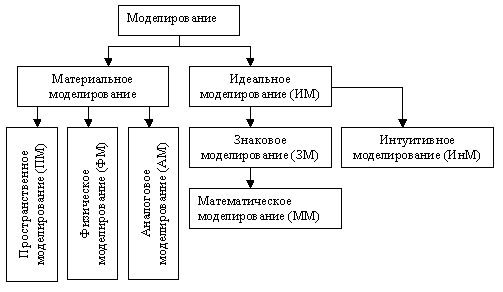
Материальным моделирование называется в том случае, когда копия объекта — модель имеет материальный характер.

В материальном моделировании можно выделить три группы методов: пространственное, физическое и аналоговое.

Пространственное моделирование изучает геометрические свойства объекта (макеты, карты, глобус).

Физическое моделирование служит для воспроизведения и изучения динамических свойств объектов (летательных аппаратов, технических сооружений).

В аналоговом моделировании изучаемый объект заменяется объектом другой физической природы, поведение которого описывается теми же математическими соотношениями, что и изучаемого объекта. Например, механические колебания изучают с помощью электрической системы, более простой и дешевой, чем ее механический аналог. Так поступают при изучении колебаний мостов.

Идеальное моделирование основывается не на материальной аналогии модели и изучаемого объекта, а на идеальной, мыслимой связи между ними. Материальной копии не создается.

Методы идеального моделирования можно разбить на две группы: формализованное (знаковое) и неформализованное (интуитивное) моделирование.

В формализованном моделировании реальный объект заменяется системой знаков (схемы, графики, чертежи, формулы).

Важнейшим видом знакового моделирования является математическое моделирование. В этом случае копия моделируемого объекта (модель) представляет собой некоторые математические соотношения (уравнения, зависимости) между параметрами системы. Задавая значения одних параметров и находя из этих соотношений другие, интересующие исследователя параметры, можно тем самым проводить эксперименты с математической моделью.

Математическое моделирование с получением количественных результатов при помощи ЭВМ получило название вычислительного эксперимента. Возможности вычислительного эксперимента часто превышают возможности материального, натурного моделирования. В некоторых случаях удается провести вычислительный эксперимент тогда, когда натурный в принципе невозможен (ядерная физика, астрофизические исследования, поведение экономических систем).

Интуитивное моделирование — основано на построении мысленной копии объекта. Каждая наука стремится заменить интуитивное представление об изучаемых объектах формализованным, знаковым представлением. На этом пути перспективным является сочетание использования экспертных знаний специалистов и математических методов принятия решений.