Метод подбора решения некорректно поставленных задач

Широко распространенным в вычислительной практике способом приближенного решения уравнения (2; 0,1) является метод подбора. Он состоит в том, что для элементов z некоторого заранее заданного подкласса возможных решений М (МОF) вычисляется оператор Az, т. е. решается прямая задача. В качестве приближенного решения берется такой элемент z₀ из множества М, на котором невязка r_U(Az, u) достигает минимума, т. е.

r_U(Az₀, u)=inf r_U(Az, u)

zОM.

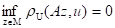
Пусть правая часть уравнения (2;0,1) известна точно, т. е. и=u_T, и требуется найти его решение z_T. Обычно в качестве М берется множество элементов z, зависящих от конечного числа параметров, меняющихся в ограниченных пределах так, чтобы М было замкнутым множеством конечномерного пространства. Если искомое точное решение z_T уравнения (2; 0,1) принадлежит множеству М, то и достигается эта нижняя граница на точном решении z_T. Если уравнение (2;0,1) имеет единственное решение, то элемент z₀, минимизирующий r_U(Az, и), определен однозначно.

Практически минимизация невязки r_U(Az, и) производится приближенно и возникает следующий важный вопрос об эффективности метода подбора, т. е. о возможности как угодно приблизиться к искомому точному решению.

Пусть {z_n} — последовательность элементов, для которой r_U(Az_n, u)—®0 при n®Ґ. При каких условиях можно утверждать, что при этом и r_F(z_n, z_T)—®0, т. е. что {z_n} сходится к z_T?

Это вопрос обоснования эффективности метода подбора.

Стремление обосновать успешность метода подбора привело к установлению общефункциональных требований, ограничивающих класс возможных решений М, при которых метод подбора является устойчивым и z_n®z_T. Эти требования заключаются в компактности множества М и основываются на приводимой ниже известной топологической лемме.

Лемма. Пусть метрическое пространство F отображается на метрическое пространство U и Uo — образ множества Fo, FoМ F, при этом отображении. Если отображение F®U непрерывно, взаимно однозначно и множество Fo компактно на F, то обратное отображение Uo®Fo множества Uo на множество Fo также непрерывно по метрике пространства F.

Доказательство. Пусть z — элементы множества F (zОF), а u—элементы множества U (uОU). Пусть функция u=j (z) осуществляет прямое отображение F®U, а функция z=y (u)—обратное отображение U®F.

Возьмем произвольный элемент u₀ из Uo. Покажем, что функция y(u) непрерывна на u₀. Предположим, что это неверно. Тогда существует такое число e₁ > 0, что для всякого d > 0 найдется элемент и¹ из Uo, для которого r_U(и¹, и₀) <d, в то время как r_F(z¹, z₀)>=—e₁. Здесь z=y (u¹), z₀=y (u₀) и z¹ОFo, z₀ОF₀.

Возьмем последовательность {d_n} положительных чисел d_n, сходящуюся к нулю при ﮥ. Для каждого d_n найдется элемент u_n¹ из Uo, для которого r_U(и_n¹, и₀)< d_n, но r_F(z_n¹, z₀)>=—e₁, где z_n¹=y (u_n¹). Очевидно, последовательность {u_n¹} сходится к элементу u₀. Так как z_n¹ принадлежат компактному на F множеству Fo, то из последовательности {z_n¹} можно выбрать подпоследовательность {Z¹n_k}, сходящуюся по метрике F к некоторому элементу z₀ ОF. При этом z₀¹№z₀, так как для всякого n_k r_F(Z¹n_k, z₀)>=—e₁, следовательно и r_F(z¹₀, z₀)>=—e₁ . Этой подпоследовательности {Z¹n_k} отвечает последовательность элементов u¹n_k=—j (Z¹n_k) из Uo, сходящаяся к u¹₀=—j (z¹₀) и являющаяся подпоследовательностью последовательности {u¹_n}. Так как последовательность {u¹_n} сходится к и₀ =j (z₀), то u¹₀=j (z¹₀)=u₀=j (z₀), т. е. j (z₀)=—j (z¹₀). В силу взаимной однозначности отображения F®U z¹₀=z₀, что противоречит ранее установленному неравенству z¹₀№z₀. Лемма доказана.

Эту лемму можно сформулировать короче.

Если отображение FoUo компакта Fo на множество Uo взаимно однозначно и непрерывно, то обратное отображение UoFo также непрерывно.

Эквивалентность этих формулировок следует из того, что замыкание F^*₀ множества Fo, компактного на F, является компактом.

Таким образом, минимизирующая последовательность {z_n} в методе подбора сходится к z_T при nҐ, если:

• а)z_T принадлежит классу возможных решений М;
• б) множество М — компакт.

Пусть оператор А непрерывен и вместо точной правой части u_T мы имеем элемент u_d такой, что r_U(u_d, u_T)<=—d, причем u_d принадлежит множеству AM (образу множества М при отображении его с помощью оператора A) и М есть компакт. Пусть {d_n} — последовательность положительных чисел таких, что d_n 0 при nоо. Для каждого п методом подбора можно найти такой элемент z^d_n, что r_U(A z^d_n, u_d)<=d_n. Элементы z^d_n будут близки к решению z_T уравнения Az=u_T. В самом деле, при отображении с помощью непрерывного оператора образ AM компакта М есть компакт и, следовательно, по лемме обратное отображение, осуществляемое оператором A^-1, непрерывно на AM. Так как.

rU(A zdn, u)<=—rU(A zn, ud)+rU(ud, uT),.

то.

rU (A zdn, uT)<=dn+d=gdn.

Из этого неравенства и из непрерывности обратного отображения АМ М следует, что r_F(z^d_n, z_T)<=—e (—g^d_n), причем e (—g^d_n)0 при g^d_n0. Таким образом, при нахождении приближения z^d_n к z_T надо учитывать уровень погрешности d правой части u_d.

На основе изложенных соображений М. М. Лаврентьев сформулировал понятие корректности по Тихонову. В применении к уравнению (2; 0,1) задача называется корректной по Тихонову, если известно, что для точного значения u=u_T существует единственное решение z_T уравнения (2; 0,1), Az_T=u_T, принадлежащее заданному компакту М. В этом случае оператор А^-1 непрерывен на множестве N=AM и, если вместо элемента u_T нам известен элемент u_d такой, что r_U(u_T, u_d)<=d и u_dОN, то в качестве приближенного решения уравнения (2; 0,1) с правой частью u= u_d можно взять элемент z_d=A^-1u_d. При d0 (u_dОN) z_d будет стремиться к z_T. Множество F₁ (F₁ М F), на котором задача нахождения решения уравнения (2; 0,1) является корректно поставленной, называют классом корректности. Так, если оператор А непрерывен и осуществляет взаимно однозначное отображение, то компакт М, к которому принадлежит z_T, является классом корректности для уравнения (2; 0,1). Таким образом, если задача (2; 0,1) корректна по Тихонову и правая часть уравнения uОAM, то метод подбора с успехом может быть применен к решению такой задачи. На первый вопрос дан исчерпывающий ответ.

Рассмотрим задачу решения интегрального уравнения Фредгольма первого рода.

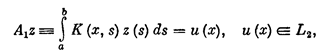
(2;1,1).

на множестве М₁ монотонно убывающих (возрастающих) и равномерно ограниченных функций |z (s)|<=B. Она корректна по Тихонову, так как множество M₁ — компакт в пространстве L₂.

Действительно, возьмем любую последовательность E= {z₁(s), z₂(s), … z_n(s), …} из M₁. Согласно теореме Хелли о выборе существуют подпоследовательность.

E₁ = {Zn1 (s), Zn2 (s), …, Znk (s), …},.

последовательности Е и функция z*(s) из множества M₁, z*(s)—ОL₂, такие, что.

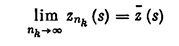
всюду, кроме, может быть, счетного множества точек разрыва функции z*(s). Из поточечной сходимости подпоследовательности Е₁ к функции z*(s) всюду, кроме, может быть, счетного множества точек, следует, как известно, сходимость подпоследовательности E₁ к функции z*(s) по метрике L₂.

Таким образом, в качестве приближенного решения на множестве М₁ уравнения (2; 1,1) с приближенно известной правой частью u¹ О АМ₁ можно брать точное решение этого уравнения с правой частью u=u¹ . Эта последняя задача эквивалентна задаче нахождения на множестве M₁ функции, минимизирующей функционал.

N[z, u1]=|| A₁z — u¹ ||²_L2 .

Пусть r_U(u_T, u¹)<=—d. Тогда, очевидно, в качестве приближенного решения уравнения (2; 1,1) можно брать функцию z_d, для которой.

|| A1zd — u1 ||2L2<= d2. (2;1,2).

Если заменить интегральный оператор A₁z интегральной суммой на фиксированной сетке с n узлами и обозначить значения искомой функции в узловых точках через z_i, то задача построения приближенного решения уравнения (2; 1,1) сведется к задаче нахождения конечномерного вектора, минимизирующего функционал N[z, и¹] и удовлетворяющего неравенству (2; 1,2).

В ряде других случаев компактные классы корректности можно указать эффективно, что дает возможность строить устойчивые приближенные решения.

В силу погрешности исходных данных элемент и может не принадлежать множеству AM. В этих условиях уравнение (2; 0,1) не имеет решения (классического) и возникает вопрос: что надо понимать под приближенным решением уравнения (2; 0,1)?

В этом случае вводится понятие квазирешения и метод подбора при условии компактности множества М позволяет найти приближение к квазирешению. В следующем параграфе вопрос о квазирешении рассматривается подробнее.