Выводы. 
Естественные модели размеров и размерностей в категориях топологии

А. С естественнонаучной точки зрения определения размерностей, и, изложенные выше по первоисточникам, в сущности сводятся к следующим выражениям:

• 1. Малая индуктивная размерность пространства Х равна n, если у каждой точки х есть сколь угодно малые окрестности, границы которых имеют размерность n-1 (в смысле). Размерность пустого множества? = 0.
• 2. Большая индуктивная размерность пространства Х равна n, если для любых его двух не пересекающихся множеств найдётся n-1- мерное замкнутое множество, разделяющее их. Также ?=0.
• 3. Размерность пространства Х, определяемая с помощью покрытий пространства Х, равна n, если минимальная кратность сколь угодно малых покрытий пространства Х равна n+1.

Таким образом, ни одно из этих утверждений, справедливых по существу нахождения величины размерности соответствующих пространств, не может являться определением размерности в логическом смысле, так как логически строгое определение категории, как это мы уже видели на примере определений категорий топологи континуума, множества, многообразия, пространства, требует подведения определяемой категории под более широкое понятие, такую категорию, которая является более общей по отношению к определяемой, отличающейся от боле общего своими частными особенностями.

В приведенных выше топологических определениях размерности указывается на принадлежность этой категории к числу, но не указывается нигде на особенности этого числа от других чисел, не являющихся размерностью (числом линий, поверхностей, точек…).

Так как и строгого логического определения категорий в силу их предельности невозможно дать, то в этом свете понятна и невозможность логического определения размерности категории… Действительно, невозможно строго логически определить атрибут категории, которая сама тоже не определена строго логически.

Б. Учитывая, что бесконечности в различных направлениях не отличаются между собой, можно в общем случае можно записать:, если обозначить через-размер-мерной фигуры со стороной-ребром. Тогда размерность пространства представляет собой показатель степени:

(10),.

(11).

В. В реальной действительности фрактальные объекты распространены гораздо шире по сравнению с объектами целочисленной размерности — одномерными сплошными непрерывными линиями, двумерными поверхностными фигурами и трёхмерными объёмными телами. В случае единичного куба Лебега, то есть при: , что даёт непосредственно:

.

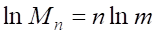
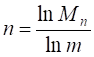
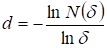
Таким образом, мы можем применять фрактальные размерности для процессов изменения размерности куба Лебега.

Г. При неизменном масштабе, так как при ,.

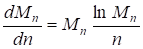
или (24).

Другими словами, на основании фрактальности геометрии многочисленных процессов мы вправе распространить самый общий топологический принцип непрерывности и на размерность тех категорий топологии, для которых этот принцип является фундаментальным.

Д. Так как функциональные связи имеют одну, общую для всех миров, форму, то вследствие различного естественного содержания различных миров возможен «дефект размера» — суть дефект того «естественного содержания» при переходе от одного мира в другой!

В этом случае такой «дефект размера» можно вычислить как определенный интеграл в пределах от до :

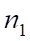
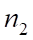
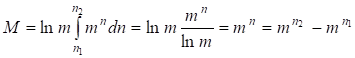
Другими словами, изменение размеров объекта при его переходе из мира одной размерности в мир другой размерности можно вычислит как разницу размеров этого объекта в этих мирах.

В процессе изменения размерности система приобретает или утрачивает часть своих свойств (при увеличении размерности — число свойств возрастает, а при уменьшении размерности — их число уменьшается соответственно).

При отображении объекта размерностью n₁ в координатной системе n₂, когда модель объекта теряет ряд своих признаков или свойств, а когда, то модель объекта приобретает несуществующие у самого объекта признаки или свойства.