Простое алгебраическое расширение поля

трансцендентный гаусс алгебраический Пусть P[x] - кольцо полиномов от x над полем P, где P — подполе поля F. Напомним, что элемент б поля F называется алгебраическим над полем P, если б является корнем какого — нибудь полинома положительной степени из P[x].

Определение. Пусть P.

Пусть бєF, P[x] - кольцо полиномов от x и P[б]= {f (б)|fє P[x] }, то есть P[б] есть множество всех выражений вида.

.

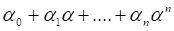
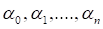
где єP и n — любое натуральное число.

Легко видеть, что алгебра { P[б], +, -, ·, 1} - подкольцо поля P (б) — является кольцом; это кольцо обозначается символом P[б].

Теорема 10. Пусть P[x] - кольцо полиномов от x над полем P и P (б) — простое расширение поля P. Пусть ш — отображение P[x] на P[б] такое, что ш (f)=f (б) для любого f из P[x]. Тогда:

для любого, а из P ш (a)=a;

ш (x)=б;

ш является гомоморфизмом кольца P[x] на кольцо P[б];

Kerш={ fє P[x] | f (б)|=0};

фактор — кольцо P[x]/ Kerш изоморфно кольцу P[б].

Доказательство. Утверждения (a) и (b) непосредственно следуют из определения ш. Отображение ш сохраняет главные операции кольца P[x], так как для любых f и g из P[x].

Ш (f+g)=f (a)+g (a), ш (fg)=f (a)g (a), ш (1)=1.

Далее, по условию, ш есть отображение P[x] на P[б]. Следовательно, ш является гомоморфизмом кольца P[x] на кольцо P[б].

Утверждение (d) непосредственно следует из определения отображения ш.

Поскольку ш — гомоморфизм кольца P[x] на P[б]. Пусть P'= P[x]/ Kerш — множество всех классов вычетов кольца P[x] по идеалу Kerш и P[x]/Kerш={P[x]/ Kerш, +, -, ·, 1'}, где 1'=1+ Kerш. Обозначим через h отображение P[x]/ Kerш в | P[б] |, определяемое следующим образом:

h ()=ш () (1).

для каждого элемента из P[x]. В силу предложения о том, что если ш — гомоморфизм кольца P[x] на кольцо P[б], то для любых a и b из P[x] равенство ш (a)=ш (b), выполняется тогда и только тогда, когда =. Значение h () не зависит от выбора представителя a в смежном классе. Далее отображение h сохраняет главные операции кольца P[x]/ Kerш. В самом деле, h (1')= и для любых, из P[x] имеем:

h (+)=h ()=ш (a+b)= ш (a)+ ш (b)=h ()+h ();

h (-)=h ()=ш (-a)=- ш (a)=- h ();

h (·)=h ()=ш (ab)= ш (a)· ш (b)= h ()· h ().

По условию, ш отображает | P[x] | на | P[б] |. В силу (1) отсюда следует, что h есть отображение множества P[x] на множество | P[б] |. Отображение h инъективно. В самом деле, в силу (1) из равенства h ()=h () следует ш (a)=ш (b); в силу того же предложения отсюда следует, что =. Следовательно, ш является изоморфизмом фактор — кольца P[x]/Kerш на кольцо P[б]. Теорема доказана.

Следствие 1. Пусть б — трансцендентный элемент над полем P. Тогда кольцо полиномов P[x] изоморфно кольцу P[б].

Доказательство. В силу трансцендентности б над P Kerш={0}. Поэтому, согласно теореме 10, P[x]/{0}P[б]. Кроме того, фактор — кольцо кольца P[x] по нулевому идеалу изоморфно P[x]. Следовательно, P[x]P[б].

Теорема 11. Пусть б — алгебраический над полем P элемент положительной степени n. Тогда любой элемент поля P[б] однозначно представим в виде линейной комбинации n элементов 1, б,…, с коэффициентами из P.

Доказательство. Пусть в — любой элемент из поля P[б]. Тогда, по теореме о минимальном полиноме над полем P, где кольцо P[б] совпадает с полем P (б) следует, что P (б)= P[б], следовательно, существует в P[x] полином f такой, что в= f (б) (1).

Пусть g — минимальный полином для б над P; в силу условия теоремы его степень равна n. По теореме о делении с остатком, существует в P[x] полином h и r такие, что.

f=gh+r,.

где r=0 (2).

или deg r < deg g=n, то есть.

r= ().

Полагая в (2) x=б и учитывая равенство (1), имеем.

. (3).

Покажем, что элемент в однозначно представим в виде линейной комбинации элементов 1, б,…,. Пусть.

() (4).

— любое такое представление. Рассмотрим полином ц.

.

Случай, когда степень ц меньше n, невозможен, так как в силу (3) и (4) ц (б)=0 и степень ц меньше степени g. Возможен лишь случай, когда ц=0, то есть. Следовательно, элемент в однозначно представим в виде линейной комбинации элементов 1, б,…,. Теорема доказана.

Пусть P — подполе поля F. Тогда мы можем рассматривать F как векторное пространство над P, то есть рассматривать векторное пространство.

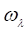
{F, +, {|лєP}},.

где — операция умножения элементов из F на скаляр лєP.

Определение. Расширение F поля P называется конечным, если F, как векторное пространство над P, имеет конечную размерность. Эта размерность обозначается через [F:P].

Предложение 1. Если б — алгебраический элемент степени n над P, то [P (б):P]=n.

Это предложение непосредственно следует из теоремы 11.

Определение. Расширение F поля P называется алгебраическим, если каждый элемент из F является алгебраическим над P.

Теорема 12. Любое конечное расширение F поля P является алгебраическим над P.

Доказательство. Пусть n — размерность F над P. Теорема, очевидно, верна, если n=0. Предположим, что n>0. Любые n+1 элементов из F линейно зависимы над P. В частности, линейно зависима система элементов 1, б,…,, то есть существуют в P такие элементы, не все равны нулю, что .

Следовательно, элемент б является алгебраическим над P. Теорема доказана.

Отметим, что существуют алгебраические расширения поля, не являющиеся конечными расширениями.