Методы решения задачи согласования временных ограничений

время программный темпоральный информация Рассмотрим методы решения ЕЗСВО и ДЗСВО. Решение ЕЗСВО в точечной алгебре (PA) основывается на преобразовании в задачу на графе, взвешенном временной информацией (TLPA-графе). TLPA-граф есть граф G=(W, E, L), где W — множество вершин, W? Ш, E={(wi, lk, wj)|wi, wjW, lkL} - множество связей (ребер), L={<,?,?} - множество возможных пометок на ребрах графа. Ребра, взвешенные ограничением V, сопоставляющая вершинам графа из множества W имена временных переменных из множества V.

Интерпретацией TLPA-графа G называется тройка, где T — упорядоченное множество; I: V>T — функция, такая, что для всех pi, pjP выполнимо, что если м (pi)=м (pj), то I (pi)=I (pj); R: L>T — функция, отображающая каждую метку lL на ребрах графа G в соответствующее бинарное ограничение R (l) на T. Моделью TLPA-графа G=(W, E, L) называется такая интерпретация, для которой справедливо: если (w1,l, w2) E — ребро в графе G, то для всех pi, pjP, таких, что м (pi)=w1 и м (pj)=w2, выполняется R (l). TLPA-граф согласован (непротиворечив), если он имеет по крайней мере одну модель. Два или более TLPA-графа логически эквивалентны, если они обладают одними и теми же моделями.

Путем длины n от вершины w0 к вершине wn в TLPA-графе G называется последовательность n ребер, которая задается набором троек (w1,l1,w2), …(wn-1,ln, wn), где wi (0?i?n) — вершины и ljL (0?j?n), (wi, li, wi+1)E. Путь в TLPA-графе называется «<-путем» («?-путем») длины n, если lj={<} (если lj={?}), при 0? j?n. «<-путь» («?-путь») в TLPA-графе называется «<-циклом» («?-циклом»), если v0=vn.

Доказано, что TLPA-граф согласован тогда и только тогда, когда он не содержит ни одного «<-цикла» и ни одного «?-цикла», содержащего две вершины, соединенные ребром, взвешенным ограничением? [4]. Таким образом, для решения задачи SAT необходимо преобразовать ЗСВО в TLPA-граф и проверить эти условия. Рассмотрим решение задачи MIN.

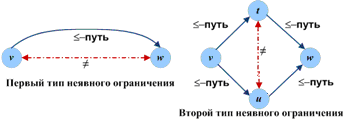
Рис. 1. Два типа неявных ограничений «меньше»

Здесь TLPA-граф согласован по путям, если для каждой пары его вершин существует не более одного соединяющего их ребра и для каждой тройки вершин u, v, w ограничение соответствующее связи (u, l, v) не противоречит ограничениям для (u, l1, w) и (w, l2, v), т. е. выполнено условие l? l1l2?.

TLPA-граф содержит в себе неявное ограничение < для вершин v и w, если не существует ни одного «<-пути» от v к w и существует либо связь (v,?, w) и «?-путь» от v к w, либо связь (t,?, u) и «?-пути» (но не «<-пути») от v к u, от u к w, от v к t и от t к w (рис. 1). Явным TLPA-графом для TLPA-графа G называется TLPA-граф, логически эквивалентный исходному графу G и не содержащий неявных ограничений. Согласованный по путям явный TLPA-граф назовем Time-графом.

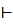
Из явного TLPA-графа G выводимо (), что:

v=w тогда и только тогда, когда v и w альтернативные имена одной и той же вершины;

v<-путь" от v к w;

v?w тогда и только тогда, когда существует «?-путь» от v к w;

v?w тогда и только тогда, когда существует «<-путь» от v к w, или существует «<-путь» от w к v, или в графе существует связь между v и w взвешенная ограничением ?.

Если произвести переход от TLPA-графа к Time-графу, то будут решены задачи SAT и MIN [4].

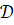
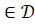
Для решения ДЗСВО осуществляется переход к задаче на дизъюнктивном графе времени (D-Time-графе) с применением алгоритма поиска с возвратами для поиска согласованного сценария (задача DSAT) или сценариев (ACS). D-Time-графом называется пара, где G=(W, E, L)-Time-граф; ={i|i=(di1,di2,…dik)} - множество дизъюнктивных ограничений, причем i интерпретируется как (di1di2…diu), dij={(xl, rl, yl)|xl, ylW, rlBTR} - множество точных ограничений. Определим множество ограничений в точечной алгебре M так, что для каждого i в M входит один из diji. Будем считать D-Time-граф согласованным, если существует такое множество M, что TLPA-граф G*=(W, EM, L) является согласованным. M назовем реализацией множества дизъюнктивных ограничений для графа G. Для решения задачи DSAT необходимо убедиться в существовании хотя бы одной реализации, для решения задачи ACS — найти все возможные реализации.

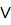
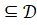
Предложено два способа уменьшения сложности ДЗСВО — упрощение задачи и уменьшение размерности задачи для алгоритмов поиска с возвратами. В первом случае вводится ограниченная ДЗСВО (ОДЗСВО), в которой устанавливается ограничение на размер элементов i множества. Во втором случае осуществляется сокращение множества по правилам сокращения пространства поиска [14]. Множество бинарных PA-дизъюнкций уменьшается до его подмножества ' за счет определения противоречий между точными и дизъюнктивными ограничениями. Алгоритм решения задачи DSAT разбивается на три этапа: на первом этапе решается ЕЗСВО Z с получением Time-графа G, на втором — осуществляется сокращение исходного множества дизъюнкций до его подмножества ', на третьем — применяется алгоритм поиска с возвратами.

В ИСППР, ориентированных на работу в открытых и динамически изменяющихся ПО, часто требуется модифицировать множество временных ограничений. При этом в интервалах между изменениями необходимо выдавать ответы на запросы о согласованности (задача SAT) и вычислять выполнимые ограничения (задача MIN). Кроме того, при решении ДЗСВО требуется периодическое изменение решенной ЕЗСВО, полученной на основе точных ограничений, по мере вычисления дизъюнктивных ограничений. В этой ситуации целесообразно использовать принцип пошагового анализа модификаций, выполняемых в исходной сети временных ограничений, позволяющий сократить ряд этапов решения ЗСВО. Если применять для решения ЗСВО после каждого из m изменений базовые алгоритмы, то сложность вычислений можно оценить величиной O (m), где — сложность решения ЗСВО на одном шаге. В данной работе предлагается способ решения задачи в таких условиях за меньшее время.

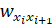
Путем рxy=из вершины x в вершину y в графе G называется последовательность вершин, в которой x0=x, xk=y и (xi, xi+1)E для всех 0? i.

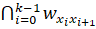
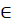
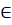
Определим P — множество всех направленных путей между всеми вершинами в графе G. Число возможных элементов в P не превышает значение e2, где e — число ограничений, входящих в E. Определим: P' - множество существенных путей в графе G, P’P; множество входящих в вершину x путей Lp (x)={рlx|l?x, рlxP'} и множество выходящих из вершины x путей Rp (x)={рxm|m?x, рxmP'}. Предложен алгоритм вычисления выполнимого ограничения между временными переменными x и y (алгоритм 1), сложность которого составляет O (max (|Rp (x)|,|Rp (y)|,|Lp (x)|,|Lp (y)|)) при условии, что множества Rp и Lp могут быть вычислены за время O (k), где k константа.

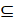
Алгоритм 1. Алгоритм вычисления выполнимого ограничения Входные данные: x, y-моменты времени; P'-множество всех существенных путей.

Выходные данные: выполнимое ограничение для переменных x и y.

• 01: ForwardPatches < Rp (x)? Lp (y)
• 02: RearwardPatches < Rp (y)? Lp (x)
• 03: Rxy =
• 04: Ryx =
• 05: return Rxy? Ryx

Алгоритмы создания (алгоритм 2) и удаления ограничений строятся так, что они выполняются над множеством существенных путей и что ограничения, которые могут привести к несогласованности, отсекаются на этапе внесения. Сложность алгоритма 2 оценивается величиной O (|Rp (y)||Lp (x)|), требуемый для работы объем памяти — O (e2). В результате работы алгоритма 2 в множество существенных путей заносятся существенные пути, которые образуются в TLPA-графе в результате создания связи (w, l, v). Сложность алгоритма удаления ограничения существенно выше сложности алгоритма 2 и оценивается в худшем случае величиной O (e2). Алгоритмы пошагового уточнения решения построены так, что они позволяют поддерживать в актуальном состоянии множество всех существенных путей на TLPA-графе G, соответствующему ЗСВО, после каждого изменения. В результате может быть получен только согласованный граф.

Основным преимуществом предложенного подхода является то, что после каждого изменения не требуется вызов дополнительных алгоритмов проверки согласованности и вычисления неявных ограничений. Как показывают тесты (рис.2) это позволяет добиться существенной экономии времени.

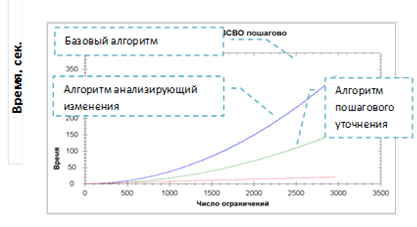
Рис. 2. Экспериментальное сравнение алгоритмов решения ЗСВО

Алгоритм 2. Алгоритм создания ограничений Входные данные: x, y — моменты времени, r — ограничение, r{,?,?}; P' - множество всех существенных путей в графе G.

• 01: r'< Алгоритм 2(x, y, P')
• 02: if (r'?r=Ш) return inconsistent // найдена несогласованность

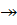
• 03: if (r'r) return // Существующее ограничение сильнее вносимого
• 04: foreach (рlxLp (x)) { // Вычисление существенных путей
• 05: if ((w (рly)?U)(w (рly)?Ш)) P' = P' рly //

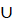
рly существенный.

• 06: foreach (рymRp (y)) if ((w (рlm)?U)(w (рlm)?Ш)) P' = P' рlm }
• 07: foreach (рymRp (y)) if ((w (рxm)?U)(w (рxm)?Ш)) P' = P' рxm