Структурная схема ПЭВМ

На рисунке изображена структурная схема ПЭВМ, которая содержит следующие основные компоненты:

• 1) ЦП — центральный процессор, который управляет работой ПЭВМ, а и выполняет все вычисления;
• 2) ОЗУ — оперативное запоминающее устройство, в котором располагаются программы, выполняемые ПЭВМ, используемые программами данные.
• 3) ПЗУ — постоянное запоминающее устройство, в котором располагаются программы, выполняемые ПЭВМ при своём включении.

Схема содержит следующие компоненты, которые предназначены для связи ПЭВМ с внешними устройствами:

• 1) Контроллер дисплея — позволяет подключить процессор к видео контрольному устройству, обеспечивает передачу видеоинформации и переключение видеорежимов дисплея;
• 2) Контроллер клавиатуры — позволяет подключить процессор к устройству ручного ввода информации, обеспечивает опрос каждой клавиши и передаёт процессору код нажатой клавиши;
• 3) Порты ввода — вывода, через которые процессор обменивается данными с внешними устройствами, предназначены для подключения к ним внешних устройств, таких как принтер, динамик, внешние устройства памяти;
• 4) Контроллер накопителя на диске — связывает накопители внешней оперативной памяти с ОЗУ, обеспечивает приём, передачу информации от носителя;

На схеме показаны следующие внешние устройства ПЭВМ:

• 1) Дисплей — основное средство оперативного вывода информации, предназначен для вывода текстовой или графической информации на экран.
• 2) Клавиатура — стандартное устройство ввода информации, основное средство взаимодействия пользователя с ПЭВМ.
• 3) Принтер — устройство печати текстовой и графической информации.

Принтеры бывают 3х типов — матричные, струйные и лазерные.

• 4) Накопитель на гибких магнитных дисках — устройство внешней памяти — служит для долговременного хранения информации — программ, архивных данных и т. д. Ёмкость носителя и скорость передачи данных незначительная.
• 5) Накопитель на жёстких магнитных дисках — устройство внешней памяти — служит для долговременного хранения информации — программ, архивных данных и т. д. Ёмкость носителя и скорость передачи данных высокая.

Задача 1.

Выполнить расчет максимальной мощности двигателя автомобиля и расчет внешней характеристики двигателя при следующих начальных условиях:

РЕШЕНИЕ.

Максимальная мощность двигателя тягача по условию обеспечения заданной максимальной скорости рассчитывается по формуле:

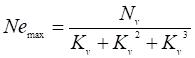
(1).

где Ne_max- искомая максимальная мощность, кВт;

N_v — мощность на режиме максимальной скорости, кВт;

K_v — отношение частоты вращения коленчатого вала двигателя при максимальной скорости движения тягача к номинальной частоте вращения:

.

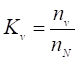
n_N— частота вращения коленчатого вала двигателя на режиме максимальной мощности (номинальная), мин^-1

n_v— частота вращения коленчатого вала двигателя при максимальной скорости автомобиля, мин^-1.

Мощность на режиме максимальной скорости определяется по формуле (3):

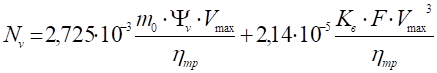
(2).

где m₀ — масса тягача, кг;

Ш_v — суммарный коэффициент сопротивления дороги;

V _max — заданная максимальная скорость тягача;

з_тр — КПД трансмиссии;

K_в — коэффициент сопротивления воздуха, кг/м³;

F — лобовая площадь тягача, м².

Внешняя характеристика двигателя представляет собой зависимость мощности, крутящего момента от частоты вращения коленчатого вала двигателя при полном открытии заслонки карбюратора.

При известном значении максимальной мощности Ne_max мощность в любой другой точке характеристики может быть найдена по формуле Лейдермана:

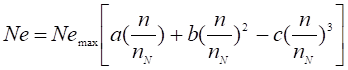
(3).

где Ne — мощность двигателя при произвольном значении частоты вращения коленчатого вала, кВт;

Ne_max — максимальная мощность двигателя, кВт;

n — заданная частота вращения коленчатого вала, мин^-1;

n_N — частота вращения коленчатого вала на режиме максимальной мощности, мин^-1;

a, b, c — коэффициенты, принимаемые для бензиновых двигателей, равны 1.

Крутящий момент в любой точке характеристики определяется по формуле:

Me=9549 (Ne/ n). (5).

Составим схему алгоритма. В алгоритме будет три блока: ввод исходных данных, расчет по формулам (1)-(5) и вывод результата.

По приведенной блок-схеме была составлена программа, листинг которой приведен ниже.

program lab1;

var m0, vmax, Ke, F, Fv, nN, Ky, n_tr:real; {peremennye — ishodnye dannye}.

Nv, Ne_max, n_v, Ne, Me: real; {peremennye — rezultaty}.

BEGIN.

—————VVOD ISHODNYH DANNYH—-;

writeln ('Vvedite ishodnye dannye:');

write ('m0=');readln (m0);

write ('Vmax=');readln (Vmax);

write ('Ke=');readln (Ke);

write ('F=');readln (F);

write ('Fv=');readln (Fv);

write ('nN=');readln (nN);

write ('Ky=');readln (Ky);

write ('n_tr=');readln (n_tr);

————-RASCHET————————-;

Nv:=2.725E-03*m0*Fv*Vmax/n_tr+2.14e-05*Ke*F*sqr (Vmax)*Vmax/n_tr;

Ne_max:=Nv/(Ky*(1+Ky*(1+Ky)));

n_v:=Ky*nN;

Ne:=Ne_max*(n_v/nN+sqr (n_v/nN)-sqr (n_v/nN)*n_v/nN);

Me:=9549*(Ne/n_v);

————-VIVOD REZULTATA————-;

writeln ('Nv=', Nv);

writeln ('Ne_max=', Ne_max);

writeln ('n_v=', n_v);

writeln ('Ne=', Ne);

writeln ('Me=', Me);

End.

Решение этой же задачи было проведено в ЭТ Excel. Ниже представлен лист с решением и результатами.

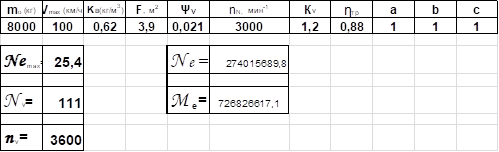
Задача 2.

Вычислить функцию, для с шагом .

РЕШЕНИЕ Выполним схему алгоритма.

Эта схема была реализована на языке Паскаль в трех вариантах: были задействованы циклы с предусловием, с постусловием и с параметром. Листинги программ приведены ниже.

а) Цикл с постусловием.

program lab21;

var x, f: real;

begin.

x:=-7;

repeat.

if x<-7 then f:=sin ((3.14/12)*x).

else.

if x<=-3 then f:=2*cos ((3.14/6)*x+(3.14/12)).

else.

f:=5* sin ((3.14/12)*x);

writeln ('f (', x:3:1,')=', f:6:2);

x:=x+1;

until x>0;

readln;

end.

б) Цикл с предусловием.

program lab22;

var x, y: real;

begin.

x:=-7;

while x<=0 do.

begin.

if x<-7 then y:= sin ((3.14/12)*x).

else.

if x<=-3 then y:= 2*cos ((3.14/6)*x+(3.14/12)).

else.

y:= 5* sin ((3.14/12)*x);

writeln ('f (', x:3:1,')=', y:6:2);

x:=x+1;

end;

readln;

end.

в) Цикл с параметром.

program lab23;

var.

x, y, a, b, h, n1: real;

n, i: integer;

begin.

x:=-7;

a:=-7;b:=0;h:= 1;

n1:=(b-a)/h; n:=round (n1);

for i:=0 to n do.

begin.

if x<-7 then y:= sin ((3.14/12)*x).

else.

if x<=-3 then y:= 2*cos ((3.14/6)*x+(3.14/12)).

else.

y:= 5* sin ((3.14/12)*x);

writeln ('f (', x:3:1,')=', y:6:2);

x:=x+1;

end;

readln;

end.

Решение этой же задачи было проведено в Excel. При вычислении функции использовалась логическая функция ЕСЛИ. Лист с решением задачи размещен ниже.

Задача 3.

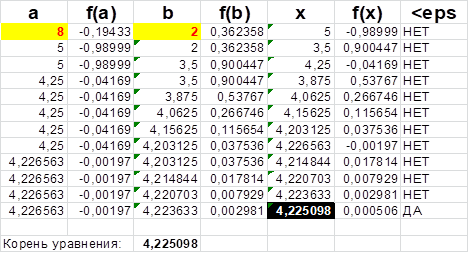
Применить метод деления отрезка пополам на интервале и найти с точностью корни уравнения .

РЕШЕНИЕ Алгоритм метода половинного деления заключается в следующем:

• 1. Выбрать нулевое приближение x₀=(a+b)/2.
• 2. Если f (x₀)=0, то x₀ очевидно является корнем уравнения.
• 3. Если f (x₀)?0, то проверить условия f (x₀)Чf (a)<0 и f (x₀)Чf (b)<0 и выбрать тот из отрезков [a, х₀], [х₀, b], на границах которого выполнено одно из этих условий (т.е. функция f (х) имеет на концах отрезка противоположные знаки).
• 4. Выбранный отрезок вновь разделить пополам и вычислить значение x₁.
• 5. Для х₁ проверить условие f (х₁)=0 и, если оно не выполняется, вернуться к п. 4.
• 6. Процесс деления отрезков пополам продолжить до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше .
• 7. Принять, что условие f (x_k)= 0 выполнено, если

Ниже приведены блок-схема алгоритма и листинг программы на языке Паскаль.

Program lab3;

function f1 (x: real): real;

begin.

f1:=cos (0.2*x*x-2);

end;

var.

x, a, b, e: real;

iteraz: integer;

begin.

write ('Input a = '); readln (a);

write ('Input b = '); readln (b);

write ('Input e = '); readln (e);

iteraz:=0;

x:=(a+b)/2;

while (f1(x)0) and (abs (a-b)>e) do.

begin.

x:=(a+b)/2;

iteraz:=iteraz+1;

if (f1(a)*f1(x))<0 then b:=x.

else a:=x;

writeln ('n=', iteraz,' x=', x:3:6,' f (x)=', f1(x):3:6);

end;

readln;

end.

Решение этой задаче было проведено и в MS Excel. Лист с решением задачи и ответом приведен ниже.

Задача 4.

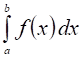
Вычислить определенный интеграл методом прямоугольников: или трапеций, на выбор.

, , ,.

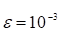
с точностью. Формула метода прямоугольников:

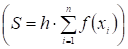
Формула метода трапеций:

.

алгоритм персональный компьютер трапеция РЕШЕНИЕ Алгоритм метода трапеций заключается в следующем:

1. Отрезок [a, b] разбивается на n равных частей.

2. Интеграл представляет собой площадь криволинейной трапеции, ограниченной осью OX, прямыми x=a и x=b и графиком функции. Очевидно, что интеграл от функции на отрезке равен сумме интегралов от этой же функции на каждом из маленьких отрезков, полученных в результате разбиения. Но на каждом из маленьких отрезков мы приближенно заменяем площадь криволинейной трапеции на площадь прямолинейной трапеции с основанием (высотой), равным длине маленького отрезка, и высотами (основаниями) f (x_n) и f (x_n+1), где x_n — левая граница отрезка, x_n+1 — правая граница отрезка. Основание (высота трапеции) равно (b-a)/n, и таким образом площадь трапеции равна (f (x_n)+f (x_n+1))(b-a)/2n. У нас всего n трапеций, причем каждые две соседние трапеции имеют одинаковые высоты (основания). Таким образом, в сумму каждое из f (x_n) кроме f (a) и f (b) войдет дважды, и таким образом весь интеграл вычисляется как, где .

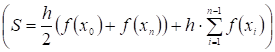
• 3. В методе трапеций не определен шаг (количество отрезков разбиения). Очевидно, что чем больше количество отрезков, тем более точным будет результат. Поэтому, задаем начальное значение n (например n=10) и вычисляем интеграл.
• 4. После этого удваиваем n и снова вычисляем интеграл (п. 2). Сравнивая полученные результаты, делаем вывод, достигнута ли требуемая точность.
• 5. Если результаты отличаются друг от друга меньше чем на е, то требуемая точность достигнута. Если нет, то снова удваиваем n и вычисляем интеграл еще раз (возвращаемся к п. 4).

Ниже представлена блок-схема алгоритма и листинг программы.

program pr4;

uses crt;

var.

h, a, b, S, dS, P, x, eps: real;

n, i: integer;

function f (x:real): real;

begin.

f:=0,1*sin (0.1*x+0.0025*x*x)/cos (0.1*x+0.0025*x*x);

end;

begin.

clrscr;

writeln ('input a, b, n, eps, please');

write ('a');

readln (a);

write ('b');

readln (b);

write ('n');

readln (n);

write ('eps');

readln (eps);

s:=0;

repeat P:=S;

h:=(b-a)/2;

S:=0;

x:=a;

for i:= 1 to n do.

begin.

x:=x+h;

S:=S+f (x);

end;

S:= S*h;

write ('n=', n:3,' h=', h:12:9);

n:=n*2;

until abs (P-S)/(s*100).

writeln;

writeln ('Result S=', S:10:6,' dS=', dS:12:9);

writeln;

writeln ('Process ended');

writeln ('Press any key to exit');

repeat until keypressed;

end.

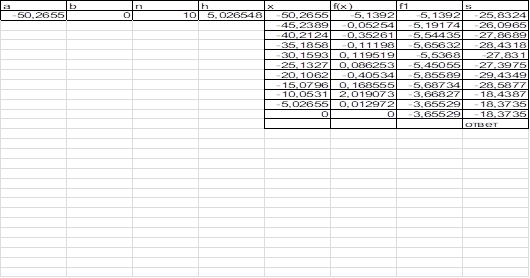
Данная задача была решена также в MS Excel. Лист с решением задачи приведен ниже. Требуемая точность была достигнута при n=10.

Программа выполненная на языке Microsoft Visual Basic 6.0.

Private Sub Command1_Click ().

Dim i As Integer.

Dim x (1 To 40) As Double.

Dim f (1 To 40) As Double.

Dim f1(1 To 40) As Double.

Dim s (1 To 40) As Double.

a = -6 * 3.14.

b = 0.

e = 0.1.

n = 40.

h = (b — a) / n.

i = 1.

x (i) = a.

f (i) = 0.1 * Tan (0.1 * x (i) + 0.025 * x (i) ^ 2).

f1(i) = f (i).

s (i) = h * f (i).

For i = 2 To n.

x (i) = x (i — 1) + h.

f (i) = 0.1 * Tan (0.1 * x (i) + 0.025 * x (i) ^ 2).

f1(i) = f1(i — 1) + f (i).

s (i) = h * f1(i).

Next.

For i = 1 To n.

Print «s=»; s (i).

Next.

If Abs (s (n) — s (n — 1)) < e Then Print «удвойте n» .

End Sub.

Private Sub Form_Load ().

End Sub.

Задача 5.

Дана прямоугольная матрица Ci, j, размером 5*5. Если данная матрица является квадратной, найти сумму элементов главной диагонали, в противном случае найти сумму всех членов матрицы.

РЕШЕНИЕ Составим схему алгоритма.

Program Lab₅;

uses crt;

var.

i, j,5,5:integer;

b, a: array[1.10,1.10] of real;

s: real;

begin.

clrscr;

write ('chislo stolbcov 5='); Readln (5);

write ('chislo strok 5='); readln (5);

begin.

if 5=5 then.

s:=0;

for i:= 1 to 5 do.

begin.

for j:= 1 to 5 do.

begin.

write ('a[', i,',', j,']='); readln (a[i, j]);

end;

writeln;

end;

begin.

if i=j then s:=s+a[i, j];

writeln (s:6:3);

end;

if ij then.

begin.

s:=0;

for i:= 1 to 5 do.

begin.

for j:= 1 to 5 do.

begin.

s:=s+a[i, j];

end;

writeln (s:6:3);

end;

end;

readln;

end;

end.

Данная задача была решена также в MS Excel. Лист с решением задачи приведен ниже.