Решение задач одномерной оптимизации методом полного перебора

Цель работы: изучение метода полного перебора для решения задач минимизации функций одной переменной.

Теоретические сведения.

Пусть требуется найти наименьшее значений целевой функции.

переменная математический неопределенность аппроксимация.

U=f (x)* ,.

заданной на отрезке [a, b]. Для решения поставленной задачи возьмем некоторое целое число n, и вычислим шаг h=(b-a) и определим значение целевой функции F (x) в точках.

xk=a+k*h (k=0,1,2,…n): Uk=f (xk).

После этого среди полученных чисел Uk найдем наименьшее число :

mn=min (U0,U1,…Un).

число mn можно приближенное принять за наименьшее значение функции f (x) на отрезке [a, b]. При этом очевидно, что.

mn? m=min f (x),.

где х принадлежит промежутку [a, b].

Однако благодаря непрерывности функции f (x) будем иметь т. е. с увеличением числа точек n ошибка, которую мы будет допускать, принимая mn за m, стремиться к нулю Всегда можно указать такую непрерывную функцию, что для нее mn будет отличаться от m больше чем на ?. Справедливость такого утверждения показана на рисунке 1.

Рисунок 1 График многоэкстремальной целевой функции.

Пусть априори известно, что целевая функция U = f (x) имеет на отрезке [a, b] только один минимум, т. е. является унимодальной (рис. 2.). Это свойство целевой функции позволяет избежать пропуска фактического минимума при решении задач оптимизации, кроме того, объем вычислений также может быть сокращен.

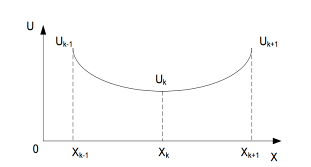
Рисунок 2 График унимодальной целевой функции.

Для решения задачи оптимизации в этом случае может быть применен следующий прием. Возьмем некоторый шаг h и будем последовательно вычислять значение функции f (x) в точках.

х0=а; х1=a+h; x2=a+2h,.

сравнивая при этом получаемые числа U0, U1, U.

Сначала они будут убывать: U0>U1>U2 …, однако в дальнейшем найдется такая точка.

xk=a+kh,.

что для значения функции в этой точке.

Uk = f (xk).

будут справедливы следующие неравенства:

Uk-1? Uk, Uk+1? Uk.

Это означает, что минимум функции достигается на отрезке [xk-1, xk+1] и его приближенно можно принять равным.

Uk = f (xk).

Для повышения точности решения задачи можно уменьшить шаг h и повторить описанную процедуру уже для отрезка [xk-1, xk+1]. В задачах управления часто требуется найти с заданной точностью е не само значение минимума целевой функции на отрезке [a, b], а абсциссу точки минимума.

x* = arg m,

т. к. x обычно играет роль управляющего воздействия, которое, конечно, должно быть оптимальным. В этом случае задача выбора числа n, необходимого для отыскания с заданной точностью е абсциссы точки минимума x*, решается так.

Следует заметить, что интервал значений x, в котором заключен оптимум целевой функции, называется интервалом неопределенности. В начале решения задачи этот интервал имеет длину (b-a). При решении задачи методом перебора первоначальный интервал неопределенности сужается до двух шагов, т. е. окончательный интервал неопределенности будет равен 2h (рис. 3.).

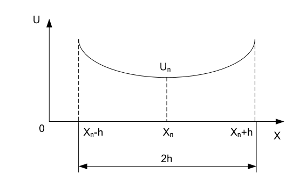
Рисунок 3 Окончательный интервал неопределенности.

Последнее означает, что x* принадлежит [xn-h, xn+h], где xn=arg mn или, что-то же самое,.

xn — h? x* ?xn — h.

Поэтому.

— h? x* - xn? h.

Или

|x* - xn|? h.

Но по условию задачи требуется, чтобы.

|x* - xn|? ?.,.

следовательно, шаг h должен удовлетворять следующему условию: h? е. Или.

(b-a)/n? е ;

n?(b-a)/ е.

Данное соотношение и определяет необходимое значение числа n. Заметим, что задача поиска может быть сформулирована и так: требуется найти абсциссу точки минимума x*, причем длина окончательного интервала неопределенности не должна превышать заданного, достаточно малого положительного числа е. В этом случае, очевидно, что n следует выбирать по соотношению.

n?2(b-a)/ е.

Выполнение.

Вариант 2.

Задание 1.

U = x2+k1*exp (k2*x).

k1= 2, k2= -0,65, [a, b] = [-10,10].

Программа:

#include.

#include.

int main (void).

{double k1=2;

double k2=-0.65;

double a=-10,b=10,e=0.001;

double min, x, g, n, h;

n=(b-a)/e;

h=(b-a)/n;

for (double i=a;i<=b;i=i+h).

{g=(i*i)+k1*exp (i*k2);

if (i==-10).

{min=g;

x=i;}.

else.

{if (g.

{min=g;

x=i;}}}.

printf («x=%fl min=%fl», x, min);

return 0;}.

Результат работы программы:

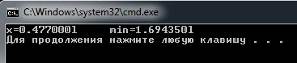
Рисунок 4.

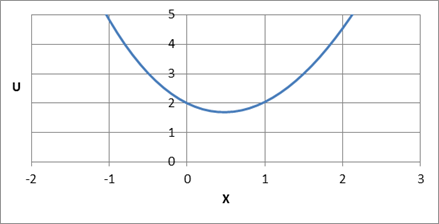
Рисунок 5 График исследуемой функции.

Минимум примерно находится в точке Umin = 1,7, что соответствует значению, найденному в программе.

Задание 2.

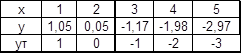
Рисунок 6.

[a, b] = [-5,5], ут = k * x + 2.

#include.

#include.

using namespace std;

int main ().

{.

int A = -5, B = 5, n;

double e = 0.01, min = 100, kk, U;

double X[5] = { 1, 2, 3, 4, 5 };

double Y[5] = { 1.05, 0.05, -1.17, -1.98, -2.97 };

n = (B — A) / e;

for (double k = A; k <= B; k += (double)(B — A) / n) {.

double U = 0;

for (int i = 0; i < 5; i++).

U += (Y[i] - (k*X[i] + 2))*(Y[i] - (k*X[i] + 2));

if (U < min) {.

kk = k;

min = U;

} }.

cout ««kk=» «kk «» «;

cout ««min=» «min «» «;

}.

Результат работы программы:

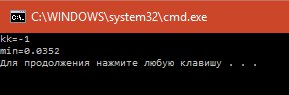
Рисунок 7.

Рисунок 8 График идентифицируемой модели объекта управления.

Экспериментальная и теоретическая зависимости почти идеально накладываются друг на друга.

Вывод: В задании 1 при использовании графического метода и метода полного перебора можно найти примерно равные значения минимума целевой функции.

В задании 2 из графика (рис. 5) видно, что экспериментальная прямая имеет вид аппроксимирующей функции, следовательно, метод полного перебора можно применять для аппроксимации модели объекта управления.