Проектирование.
Подсистема прогноза снабжения энергетическими ресурсами теплогенераторных станций

Средняя абсолютная процентная ошибка прогнозирования является абсолютной мерой качества прогнозов в том смысле, что позволяет оценить его независимо от других прогнозов: достаточно выбрать некий уровень средней ошибки (например, 5%) и сравнивать рассчитанное по статистике значение с этим тестовым уровнем. Если расчетное значение меньше тестового, то прогноз считается хорошим, если больше — плохим. Читать ещё >
Проектирование. Подсистема прогноза снабжения энергетическими ресурсами теплогенераторных станций (реферат, курсовая, диплом, контрольная)
Разработка обобщённой подсистемы прогнозирования
Согласно аналитическому обзору, для решения задачи прогнозирования температуры окружающей среды в рамках управления производством тепловой энергии на теплогенераторных станциях наиболее востребованными методами прогнозирования являются фактографические методы.
Точность прогнозирования при этом должна обеспечиваться за счет предоставления подсистеме прогнозирования исходных данных о температуре окружающей среды за прошедшие периоды времени.
Таким образом, работа подсистемы прогнозирования представляет собой следующие действия:
- 1) получение накопленного массива данных о температуре окружающей среды за некоторый квант времени;
- 2) сглаживание полученного временного ряда наблюдений;
- 3) аппроксимация и формирование нового ряда;
- 4) прогнозирование и экстраполяция.
Временным рядом называется последовательность значений, изменяемых во времени. Временной ряд позволяет наблюдать всю историю изменения величины и даёт возможность судить о её «типичном» поведении, а также об отклонениях от такого поведения.
В отличие от анализа случайных выборок, анализ временных рядов основывается на предположении, что последовательные значения в массиве данных наблюдаются через равные промежутки времени.
Большинство регулярных составляющих временных рядов являются либо трендом, либо сезонной составляющей. Тренд — общая систематическая линейная или нелинейная компонента, которая может изменяться во времени. Сезонная составляющая — это периодически повторяющаяся компонента. [4].
Описание модели временного ряда температуры воздуха окружающей среды состоит в следующем:
- 1) длительность наблюдения данных — от одного года;
- 2) промежутки наблюдения данных — 1 сутки или 1 месяц;
- 3) присутствует сезонная составляющая: повышение температуры в летние периоды времени и понижение температуры в зимние периоды.
Одними из самых популярных методов для оценки параметров временного ряда и прогнозирования его данных являются:
- 1) метод авторегрессии проинтегрированного скользящего среднего (АРПСС). Данный метод имеет высокую мощность и гибкость, однако, благодаря этому, АРПСС — сложный метод, его не так просто использовать, и требуется большая практика, чтобы овладеть им;
- 2) экспоненциальное сглаживание. Является очень популярным методом прогнозирования. Существует несколько вариантов такого метода:
a) простое экспоненциальное сглаживание не учитывает тренд и сезонную составляющую;
b) методы, учитывающие аддитивные и мультипликативные тренд и сезонность — модель Хольта, модель Хольта-Уинтерса и модель Тейла-Вейджа;
- 3) сезонная декомпозиция (метод Census I). Тренд и циклическая компонента объединяются в одну тренд-циклическую компоненту;
- 4) сезонная корректировка X-11 (метод Census II). Метод учитывает корректировки временного ряда, такие как: поправка на число рабочих дней, резко выделяющиеся наблюдения (выбросы) и другие;
- 5) анализ распределенных лагов — это специальный метод оценки запаздывающей зависимости между рядами;
- 6) одномерный анализ Фурье. Позволяет разложить временной ряд с циклическими компонентами на несколько основных синусоидальных функций с определенной длиной волн;
- 7) кросс-спектральный анализ. Развивает одномерный анализ Фурье и позволяет анализировать одновременно два ряда.
Для решения задачи прогнозирования воспользуемся методом экспоненциального сглаживания.
Простое экспоненциальное сглаживание временного ряда осуществляется по формуле:
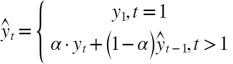
(2.1).
где — прогнозируемое значение для периода t текущего цикла;
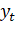
— значение временного ряда для периода t текущего цикла;
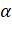
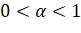
— коэффициент сглаживания, .
Простое экспоненциальное сглаживание не учитывает тренд и сезонную составляющую, поэтому его применение для поставленной задачи прогнозирования обосновано только при описании временным рядом менее двух сезонов.
Для прогнозирования значений временного ряда при описании им двух и более сезонов используем экспоненциальное сглаживание по модели Хольта-Уинтерса.
Модель Хольта-Уинтерса расширяет прогностическую модель экспоненциального сглаживания и учитывает тренд и сезонность временного ряда. [5].
Существует две вариации модели Хольта-Уинтерса в зависимости от природы сезонной составляющей: аддитивный и мультипликативный методы.
Использование аддитивного метода предпочтительно, когда сезонная составляющая временного ряда примерно постоянна для каждого цикла. Мультипликативный же метод предпочтителен, когда сезонная составляющая изменяется пропорционально значениям временного ряда в каждом цикле.
Согласно определенной модели временного ряда поставленной задачи прогнозирования ясно, что необходимо использование аддитивного варианта модели Хольта-Уинтерса. Прогнозируемые значения временного ряда y с количеством измерений в одном цикле m для горизонта прогнозирования h рассчитываются по формулам:
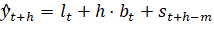
(2.2).
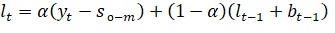
(2.3).
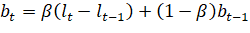
(2.4).
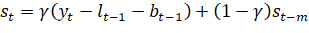
(2.5).
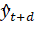
где — прогнозируемое значение для периода времени, отстающего на d шагов от последнего значения временного ряда;
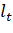
— параметр прогноза, очищенный от влияния тренда и сезонности;
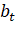
— параметр тренда периода t;
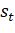
- — параметр сезонности периода t;
- — значение временного ряда для периода t;
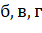
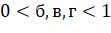
— коэффициенты сглаживания, .
Для использования формул (2.3), (2.4) и (2.5) необходима установка начальных значений по следующим формулам:
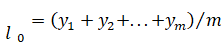
(2.6).
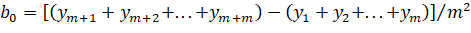
(2.7).
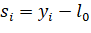
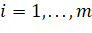
при, (2.8).
Использование метода экспоненциального сглаживания ставит перед нами новую проблему: результаты прогнозирования зависят от выбора коэффициентов сглаживания (для простого экспоненциального сглаживания и для экспоненциального сглаживания по модели Хольта-Уинтерса).
Коэффициенты сглаживания невозможно выбрать на основе одних лишь исходных данных временного ряда. Поэтому для оценки качества прогнозов применяют специальные статистические методы. [6].
К простейшим статистикам качества прогнозов относятся:
- 1) средняя абсолютная процентная ошибка (Mean Absolute Percentage Error — MAPE);
- 2) средняя абсолютная ошибка (Mean Absolute Error — MAE);
- 3) корень квадратный из средней квадратичной ошибки прогнозирования (Root Mean Squared Error — RMSE).
Средняя абсолютная процентная ошибка прогнозирования является абсолютной мерой качества прогнозов в том смысле, что позволяет оценить его независимо от других прогнозов: достаточно выбрать некий уровень средней ошибки (например, 5%) и сравнивать рассчитанное по статистике значение с этим тестовым уровнем. Если расчетное значение меньше тестового, то прогноз считается хорошим, если больше — плохим.
Две другие меры качества прогнозов (MAE и RMSE) являются относительными, то есть могут быть использованы для сравнения двух (или более) различных прогнозов одного и того же показателя между собой: лучшим считается тот прогноз, у которого значение МАЕ или RMSE меньше. При этом, очевидно, этот лучший прогноз может быть хорошим или плохим с точки зрения МАРЕ.
Главными достоинствами этих трёх статистик качества является простота их расчета и независимость от свойств ошибок прогнозирования, главным недостатком — то, что они не позволяют получить ответ на вопрос о том, являются ли два прогноза показателя разными со статистической точки зрения.
Кроме того, обычно все эти статистики не противоречат друг другу, то есть при их использовании лучшим будет выбран один и тот же прогноз, однако, наиболее часто для сравнения прогнозов используется RMSE.
Приведенные выше статистики качества рассчитываются по следующим формулам:
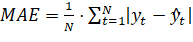
(2.9).
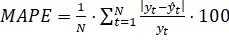
(2.10).
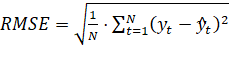
(2.11).
где N — количество измерений;
- — значение временного ряда для периода t;
- — прогнозируемое значение для периода t.
Воспользуемся статистикой качества RMSE для оценки прогноза и выбора оптимальных параметров сглаживания. Для этого в системе необходимо разработать функционал расчета RMSE с помощью перебора по сетке.
Метод перебора по сетке являясь наиболее простым и универсальным, одновременно является и самым трудоёмким методом решения задач нелинейного программирования.
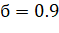
Метод перебора по сетке заключается в следующем: возможные значения параметра разбиваются сеткой с определенным шагом (например, для простого экспоненциального сглаживания возможная рассматриваемая сетка значений для коэффициента сглаживания: от до с шагом 0.1), после чего находятся значения целевой функции с использованием каждого из возможных значений в сетке и среди них выбирается наилучшее значение.
Практически метод перебора по сетке применим только при числе переменных целевой функции не больше 4, так как трудоёмкость быстро возрастает с ростом размерности задачи. Поэтому для экспоненциального сглаживания по модели Хольта-Уинтерса возможно необходимо предусмотреть дополнительное упрощение поиска оптимальных параметров сглаживания.