О создании модели расчета трещиноватых скальных массивов при тектонических нагрузках методом эквивалентных материалов

Аннотация

В статье рассматриваются вопросы, связанные с моделированием трещиноватых скальных массивов при тектонических нагрузках. Были проведены исследования в условиях лаборатории на физических моделях и математическое моделирование. Результаты этих исследований были сравнены и сделаны выводы о возможности проведения дальнейших численных экспериментах.

Ключевые слова: физическое моделирование, численное моделирование, математическое моделирование, имитационное моделирование, метод конечных элементов, напряженно-деформированное состояние.

В последние несколько десятилетий методы математического моделирования прочно вошли во все отрасли строительного производства. Подземное строительство не стало исключением. Но при этом до сих пор не разработана модель расчета, которая бы удовлетворяла всем условиям строительства. Это утверждение особенно справедливо в отношении трещиноватых скальных массивов. По этому, в 80-х годах ХХ-го столетия, специально для трещиноватых скальных грунтов был изобретен метод дискретных элементов.

Данный метод почти лишен недостатков других численных методов при решении задач, связанных с трещиноватыми скальными массивами. Но из-за своей узкой направленности метод дискретных элементов не получил столь широкого распространения, как другие методы математического моделирования, в частности метод конечных элементов (МКЭ) — самый распространенный метод моделирования в строительном производстве в целом и в подземном строительстве в частности.

Над созданием численной модели расчета скального массива и конструкций в МКЭ работали и продолжают работать многие ученые, такие как С. А. Юфин, В. Г. Орехов, М. Г. Зерцалов, С. Н. Чернышев, А. Н. Власов и другие [1,2,3,4,5,6,7]. Но всё то многообразие магматических, метаморфических и осадочных горных пород, которые относятся к классу скальные грунты, и их геомеханические условия работы не позволяют создать сколь-нибудь универсальную расчетную модель. И по этому авторы данной статьи уже несколько лет продолжают работу, которая была начата под руководством профессора, д.т.н. С. А. Юфина [8,9].

В данной фазе работы авторы создают расчетную модель для скального массива с некоторым количеством ортогональных субгоризонтальных и субвертикальных трещин с различной шириной раскрытия. В качестве заполнителя трещины имеют обломочные осадочные горные породы (глины, песок и щебень материнской горной породы). При этом на рассматриваемый массив действуют тектонические вертикальные и горизонтальные нагрузки различного сочетания. Создание расчетной модели ведется двумя способами: численным методом и физическим моделированием из эквивалентных материалов. скальный тектонический моделирование Часть результатов численных экспериментов была опубликована [10], часть результатов эксперимента еще предстоит опубликовать. В данной статье речь пойдет о втором способе исследования — физическом моделировании из эквивалентных материалов.

Физическое моделирование сооружений методом эквивалентных материалов широко применялось задолго до появления расчетов численными и компьютерными методами. С развитием высокопроизводительных персональных электронно-вычислительных машин лабораторные исследования с применением эквивалентных материалов почти сошли на нет. Но данный способ моделирования до сих пор применяют в тех отраслях строительства, где при помощи компьютерного моделирования невозможно получить результат или полученный результат с большой долей вероятности может получиться недостоверным. Также к физическому моделированию эквивалентными материалами прибегают тогда, когда необходимо сравнить полученные результаты численного моделирования с модельными исследованиями, которые, по результату, очень близки к натурным данным.

В нашем случае физическое моделирование из эквивалентных материалов применялось как раз для сравнения результатов с численным экспериментом. Эксперимент на моделях из эквивалентных материалов проводился в НОЦ «Геотехника» ФГБОУ ВПО «МГСУ», где применялся комплекс оборудования «Геотек» для трехосных исследований различных грунтов.

Исходные модели для экспериментов выполнялись из гипса, который моделировал исходную условную скальную породу. Во всех численных исследованиях применяется условная скальная порода с усредненными физико-механическими характеристиками, которые соответствуют породам с коэффициентов крепости по М. М. Протодьяконову равным 8—12. В качестве заполнителя трещины применялся структурный пластилин. При известных характеристиках эквивалентных материалов при применении масштабного коэффициента можно получить результаты, сопоставимые с численным или математическим (компьютерным) моделированием [11,12,13].

Для создания модели математического моделирования МКЭ был выбран численный образец — куб с размером стороны 10 см (рис. 1). На рис. 2 представлены модели из эквивалентных материалов для физического моделирования. В связи с тем, что оборудование «Геотек» не дает возможность проводить физическое моделирование на квадратной модели, было принято решение сделать круглую модель с системой трещин, а из численного эксперимента вычленить наиболее нагруженную область с такой же трещиной для проведения сравнительного анализа.

Рис. 1. — Система трещиноватости, принятая в исследовании

Рис. 2. — Подготовленные модели для физического моделирования

Система трещин представлена на рис. 3 и имеет наклон к плоскости оси Y под углами 0, 5, 20, 40 и 60 градусов, при этом трещины ортогональны и взаимноперпендикулярны.

Каждый образец испытывался на трехосное сжатие. Горизонтальных нагрузок было три: 200кПа, 400кПа, 800кПа и они действовали постоянно, без изменения усилия во времени. Вертикальные нагрузки менялись в широких пределах от 1:1 до 1:10 от горизонтальной в зависимости от предела прочности образца на разрушение. На рис. 3 представлен график вертикального и горизонтального загружения трещиноватых физических моделей из эквивалентных материалов.

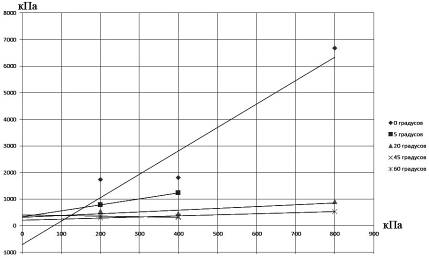
Рис. 3. — Сводный график вертикальных и горизонтальных напряжений при различных углах трещиноватости

В таб.1 приводятся результаты физического моделирования при различном наклоне трещин и его сравнение с численным моделированием. Для удобства восприятия максимальная деформация образца при физическом моделировании переведена масштабным коэффициентом миллиметры, которыми оперирует программа математического моделирования ZSOIL, с помощью которой проводили численные эксперименты.

Таблица № 1.

Трехосное испытание образца из эквивалентных материалов.

Как видно из результатов физического моделирования два эксперимента результата не имеют потому, что в самом начале эксперимента образцы разрушались и получить сколько-нибудь приемлемый результат не получилось. В связи с этим полученный результат при проведении численного эксперимента вызывает сомнение. Численный эксперимент с углом наклона трещин равный ноль градусов пока не проводился и поэтому сравнить физическое моделирование пока не с чем.

Анализируя полученные данные и сравнивая их с численным экспериментом, результаты которого представлены в работе [10], можно сделать вывод о том, что в рамках неассоциированной задачи результаты, за некоторым исключением, имеют разницу в 50%, что является неприемлемым. Следовательно, неассоциированное численное моделирование возможно применять только при углах наклона трещин в 5 и 60 градусов. Для остальных трещин надо решать ассоциированные задачи, которые будут сделаны в ближайшее время.

• 1. Юфин С. А. Механические процессы в породных массивах и взаимодействие их с подземными сооружениями. // Диссертация на соискание ученой степени д.т.н. М.: МГИ, 1991. C.409
• 2. Орехов В. Г., Зерцалов М. Г. Механика разрушений инженерных сооружений и горных пород. М.:АСВ, 1999. С.254
• 3. Чернышев С. Н. Трещины горных пород. М: Наука, 1983. С.216
• 4. Власов А. Н. Определение эффективных деформационных характеристик слоистых и трещиноватых скальных пород. // Диссертация на соискание ученой степени к.т.н. М.: МИСИ, 1990. С.280
• 5. Борисова Е. В., Васильев П. В. Идентификация трещиноподобных дефектов в составных упругих телах сложной геометрии. //Инженерный вестник Дона, № 4, 2014 URL: ivdon.ru/ru/magazine/archive/N4y2014/2671
• 6. Быков Д. В., Лихачёв Д. В. Имитационное моделирование как средство модернизации участка транспортной сети. //Инженерный вестник Дона, № 2, 2014 URL: ivdon.ru/ru/magazine/archive/n2y2014/2388
• 7. Прокопов А. Ю., Акопян В. Ф., Гаптлисламова К. Н. Изучение напряженно-деформированного состояния грунтового массива и взаимного влияния подземных конструкций существующих и вновь возводимых сооружений в береговой зоне морского порта Тамань. // Инженерный вестник Дона, № 4, 2013 URL: ivdon.ru/ru/magazine/archive/n4y2013/2104
• 8. Юфин С. А., Ламонина Е. В. Анализ напряженно-деформированного состояния трещиноватых скальных пород с использованием численных методов. // Научно-технический журнал «Горный информационно-аналитический бюллетень». № 10, 2008. С.268−277.
• 9. Ламонина Е. В. Численное моделирование трещиноватых скальных массивов. // Диссертация на соискание ученой степени к.т.н. М.: МГСУ, 2006. C.184
• 10. Влад С. В. О численном моделировании трещиноватых скальных массивов при геотектонических нагрузках. // Журнал «Промышленное и гражданское строительство». № 11, 2014. С.32−35.
• 11. Мочернюк Д. Ю. Физическое моделирование инженерных процессов. Львов: изд-во Львовского государственного университета, 1987. С.184
• 12. Rakishev B.R., Seituly K., Kovrov O.S. Physical Modeling geomechanical stability of open-cast slopes and internal overburden dumps. -In Legislation, Technology and Practice of Mine Land Reclamation. Zhenqi Hu eds. Balkema Book. 2015. P.250
• 13. Gockenbach M.S. Partial Differential Equations: Analytical and Numerical Methods. SIAM. 2010. P.170

References

• 1. Yufin S.A. Mehanicheskie processy v porodnyh massivah i vzaimodejstvie ih s podzemnymi sooruzhenijami. [Mechanical processes in pedigree massifs and their interaction with underground constructions.] Dissertacija na soiskanie uchenoj stepeni d.t.n. M.: MGI, 1991. p.409.
• 2. Orekhov V.G., Zertsalov M.G. Mehanika razrushenij inzhenernyh sooruzhenij i gornyh porod. [Mechanics of destructions of engineering constructions and rocks] M.: ASV, 1999. p.254
• 3. Chernyshev S.N. Treshhiny gornyh porod. [Cracks of rocks] M: Nauka, 1983. p.216
• 4. Vlasov A.N. Opredelenie jeffektivnyh deformacionnyh harakteristik sloistyh i treshhinovatyh skal’nyh porod. [Definition of effective deformation characteristics of layered and jointed rocky breeds] Dissertacija na soiskanie uchenoj stepeni k.t.n. M.: MISI, 1990. p.280
• 5. Borisova E.V., Vasil’ev P.V. Inћenernyj vestnik Dona (Rus), № 4, 2014. URL: ivdon.ru/ru/magazine/archive/N4y2014/2671
• 6. Bykov D.V., Lihachjov D.V. Inћenernyj vestnik Dona (Rus), № 2, 2014. URL: ivdon.ru/ru/magazine/archive/n2y2014/2388
• 7. Prokopov A. Ju., Akopjan V.F., Gaptlislamova K.N. Inћenernyj vestnik Dona (Rus), № 4, 2013. www.ivdon.ru/ru/magazine/archive/n4y2013/2104
• 8. Yufin S.A., Lamonina E.V. Nauchno-tehnicheskij zhurnal «Gornyj informacionno-analiticheskij bjulleten'». № 10, 2008. pp.268−277.
• 9. Lamonina E.V. Chislennoe modelirovanie treshhinovatyh skal’nyh massivov. [Numerical modeling of jointed rocky massifs]. Dissertacija na soiskanie uchenoj stepeni k.t.n. M.: MGSU, 2006.
• 10. Vlad S.V. Zhurnal «Promyshlennoe i grazhdanskoe stroitel’stvo». № 11, 2014. pp.32−35.
• 11. Mochernjuk D. Ju. Fizicheskoe modelirovanie inzhenernyh processov. [Physical modeling of engineering processes] L’vov: izd-vo L’vovskogo gosudarstvennogo universiteta, 1987.
• 12. Rakishev B.R., Seituly K., Kovrov O.S. Physical Modeling geomechanical stability of open-cast slopes and internal overburden dumps. In Legislation, Technology and Practice of Mine Land Reclamation. Zhenqi Hu eds. Balkema Book. 2015.
• 13. Gockenbach M.S. Partial Differential Equations: Analytical and Numerical Methods. SIAM. 2010.