К вопросу подбора арматуры безбалочных перекрытий с использованием возможностей ПК Сапфир

Аннотация

В статье рассмотрены результаты подбора арматуры монолитных железобетонных безбалочных перекрытий, отличающихся параметрами сетки конечных элементов, при прочих равных характеристиках. Конечно элементная модель создавалась средствами ПК САПФИР с последующей передачей аналитической модели в ПК ЛИРА-САПР. В процессе анализа исследовалось влияние параметров автоматической триангуляции сетки конечных элементов на площадь опорной арматуры.

Установлено, что увеличение шага триангуляции ведет к снижению требуемой по расчету площади верхней продольной арматуры. Это снижение может достигать 85%, и в случае недостаточного контроля качества сетки конечных элементов это станет причиной серьезной ошибки в расчете. При автоматической генерации сетки размер конечного элемента может значительно превышать шаг триангуляции. Во всех сетках с зоной перехода от АЖТ к плите в виде треугольников наблюдается эффект увеличения требуемой по расчету арматуры по мере отдаления от грани колонны, что на наш взгляд нелогично. Практическую ценность, как наиболее простой способ, имеет вариант разбиения плиты на прямоугольные конечные элементы с размером равным или немного большим чем сечение колонны без использования абсолютных жестких тел.

Ключевые слова: монолитный каркас, безбалочное перекрытие, триангуляция, подбор арматуры, расчет конструкций, ПК САПФИР, ПК ЛИРА-САПР.

Современные программные комплексы, поддерживающие BIM (Building Information Modeling) технологии, в частности ПК САПФИР, позволяют в автоматическом режиме осуществить переход от трехмерной модели здания к аналитической, и затем к конечно элементной модели здания [1], расчет которой ведется с использованием метода конечных элементов (далее МКЭ) [2−4]. Известно, что результаты расчета и объективность принятых на их основе выводов и решений зависят от правильности выбора типа конечных элементов (далее КЭ) и параметров сетки разбиения рассчитываемой конструкции на КЭ [5, 7 — 9]. Возможность генерации сетки КЭ в автоматическом режиме значительно облегчает работу проектировщика, но всегда ли таким образом можно получить сетку, гарантирующую получение правильного армирования? Выполненный вычислительный эксперимент и анализ полученных результатов свидетельствуют о том, что к полученной таким образом схеме следует относиться с известной осторожностью.

Опытным образцом для вычислительного эксперимента был принят фрагмент каркаса монолитного железобетонного здания с плоскими плитами (рис.1). Такой выбор объясняется популярностью данного конструктивного решения в современном строительстве. Следует отметить, что упомянутая конструктивная схема может быть реализована как с использованием бетонов обычной прочности, так и бетонов высокопрочных [6], а также с использованием композитных материалов [10].

Во всех образцах: сетка колонн 6×6м; их сечение 0,4×0,4 м; плиты толщиной 0,2 м; бетон В25; арматура А400; колонны жестко защемлены. Нагрузки: собственный вес и распределенная по площади нагрузка 5 кН/м².

Рис. 1. Схема — опытный образец:

а — вид в ПК САПФИР, б — вид в ПК ЛИРА-САПР Вычислительный эксперимент включал в себя три серии образцов, отличающихся друг от друга способом триангуляции. В первой серии использовалась адаптивная триангуляция, во второй треугольная, а в третий прямоугольная. Шаг триангуляции варьировался в достаточно широком диапазоне. В каждой из серии шаги триангуляции были одинаковы и приняты равными: 1/6; 1/10; 1/12; 1/15; 1/20 и 1/30 пролета (1,0; 0,6; 0,5; 0,4; 0,3 и 0,2 м соответственно). Узел опирания плиты на колонну моделировался как с использованием абсолютно жесткого тела (далее АЖТ), так и без него. Разбиение плиты на КЭ осуществлялось средствами ПК САПФИР, при этом в схемах с АЖТ параметр «форма АЖТ» принят «точно по форме сечения».

Предметом анализа принята площадь верхней продольной рабочей арматуры AS2 вдоль оси «Х» над колонной, расположенной на пересечении осей «Б2 и «3» (рис.2). При этом во внимание принимались наибольшие значения AS2 в ближайших к колонне конечных элементах.

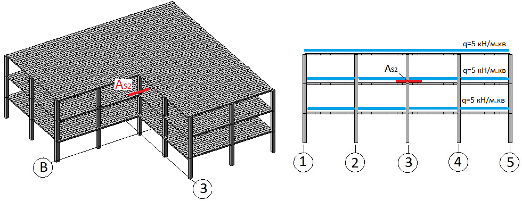
Рис. 2. Положение исследуемой площади арматуры AS2 в каркасе

арматура безбалочный перекрытие сапфир Рассмотрим сначала образцы, конечно элементная модель которых не содержит АЖТ. Установлено, что результаты, полученные с использованием прямоугольной триангуляции и адаптивной, полностью совпадают. То есть оба способа генерируют практически одинаковую регулярную сетку. Причем параметр «шаг триангуляции» здесь однозначно определяет размеры КЭ. Таким образом, в данном случае шаг триангуляции и размер КЭ можно отождествить. В случае треугольной триангуляции это не так, поскольку размер отдельных КЭ может на 20 — 25% превышать шаг триангуляции, что нужно иметь ввиду при использовании данного программного продукта.

Анализ полученных результатов подбора арматуры свидетельствует о наличии в образцах с триангуляцией прямоугольной и адаптивной ярко выраженной тенденции уменьшения требуемой по расчету арматуры AS2 по мере увеличения шага триангуляции, то есть размера КЭ. Так, при изменении шага триангуляции от 0,2 м до 1,0 м площадь арматуры снижается на 54,5%, что представляется весьма значительной величиной. Вместе с тем, в схемах с треугольной триангуляцией этого не наблюдается (рис.3), а размах значений составляет 25,9%. Очевидно, что отмеченные закономерности могут быть объяснены разным положением центров тяжести КЭ, определяющих величину AS2, при разных параметрах сетки. Дело в том, что усилия и, следовательно, площадь арматуры вычисляются в центрах тяжести КЭ.

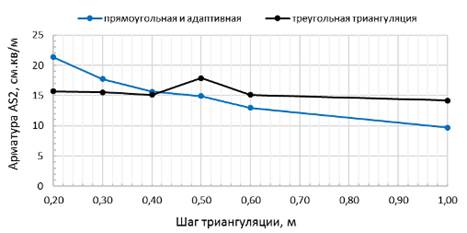
Рис. 3. Зависимость AS2 от шага триангуляции в схемах без АЖТ

Рассмотрим зависимость площади арматуры AS2 от положения центра тяжести КЭ относительно колонны. Для этого на графике рис. 4 по оси ординат отложим расстояния грани колонны до центра тяжести КЭ. Здесь отрицательным значениям этого расстояния соответствуют конечные элементы, центры тяжести которых, расположены в теле колонны. Очевидно, что соответствующие отрицательным ординатам значения площади AS2 практической ценности не имеют.

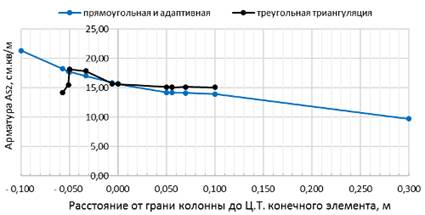
Рис. 4. Зависимость AS2 от положения центра тяжести КЭ в схемах без АЖТ

Как видим, на расстоянии 0,0 — 0,05 м от грани колонны значения площади арматуры AS2 для всех образцов практически одинаковы (разница составляет 2% - 6%), то есть практически не зависят от способа и шага триангуляции. Так, при прямоугольной и адаптивной триангуляции требуется AS2=15,63 см²/м (шаг 0,4 м). В случае треугольной триангуляции AS2=15,52 см²/м (шаг 0,3 м). Следовательно, при создании модели сетку следует генерировать так, чтобы центры тяжести опорных КЭ располагались по грани колонны, или на небольшом (до 5 см) расстоянии от неё. При прямоугольной и адаптивной триангуляции эту рекомендацию выполнить просто — достаточно принять шаг триангуляции равным сечению колонны. В случае автоматической треугольной триангуляции влиять на положение центра тяжести КЭ сложно. Поэтому предпочтительнее использование триангуляции прямоугольной и адаптивной.

Использование в узлах опирания плиты на колонну АЖТ во всех случаях ведет к образованию зоны перехода от АЖТ к полю плиты и смещению центров тяжести опорных КЭ от грани колонны к середине пролета. В зависимости от способа триангуляции, а также соотношения размеров АЖТ и шага триангуляции здесь могут образовываться как четырехугольные, так и треугольные элементы. Анализ результатов свидетельствует о наличии тенденции уменьшения площади арматуры по мере увеличения шага триангуляции (рис. 5), что ранее наблюдалось в схемах без АЖТ (рис.3).

Рис. 5. Зависимость AS2 от шага триангуляции в схемах с АЖТ

Рассмотрим образцы с прямоугольной триангуляцией. В отличие от схем без АЖТ здесь наблюдается заметное различие (на 33−58%) между шагом триангуляции и размерами отдельных конечных элементов, следовательно, параметр «шаг триангуляции» и размер КЭ отождествлять нельзя. Разброс максимальных значений A_S2 составляет 9,1 — 16,86 см²/м, то есть 85,2%. В зонах перехода от АЖТ к плите, имеющих несколько треугольников, наблюдается своеобразное распределение A_S2, выражающееся в увеличении значения A_S2 по мере удаления от грани колонны, что на наш взгляд нелогично. Дело в том, что в элементах, центр тяжести которых расположен ближе к грани колонны требуемая площадь арматуры оказывается меньше чем в элементах с центром тяжести, расположенном на большем расстоянии (рис.6), хотя должно быть наоборот. При шаге триангуляции 0,4 м обращает на себя внимание разница значений A_S2=16,9 и A_S2=15,9 см²/м, в двух треугольных КЭ, симметрично расположенных относительно оси «В» (рис. 6,в). С учетом упомянутой особенности распределения значений A_S2 в окружающих колонну треугольных КЭ при конструировании следует ориентироваться на значение A_S2=15,5 см²/м, полученное в образце с зоной перехода от АЖТ к плите, образованной прямоугольными КЭ с шагом триангуляции 0,5 м (совпадает с рис. 6.б).

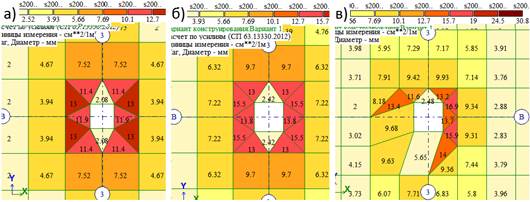
Рис. 6. Вид сетки при прямоугольной триангуляции при шаге:

а — равном 0,6 м; б — равном 0,5 м; в — равном 0,4 м В случае использования адаптивной триангуляции размеры отдельных элементов превышают шаг триангуляции на 30 — 60%. Зона перехода от АЖТ к плите в четырех случаях из шести содержит треугольные КЭ. Так, треугольные КЭ имеют место при шаге равном 1/6 пролета (рис. 7.а). Очевидно, что такую сетку нельзя признать удачной и расчетах использовать не рекомендуется. В остальном, результаты логичны — с уменьшением шага триангуляции уменьшаются размеры КЭ в их центры тяжести смещаются в направлении грани колонны. Это ведет к увеличению момента и требуемой расчетом площади арматуры (рис.7). Разброс максимальных значений A_S2 составляет: 10,2 — 15,76 см²/м, то есть 54,5%. Примечательно, что при шаге триангуляции равном 0,2 м армирование, полученное при адаптивной триангуляции и прямоугольной, полностью совпадает. При конструировании плиты назначать арматуру можно ориентируясь на значение A_S2=15,76 см²/м (шаг триангуляции 0,2 м, рис. 7,в), но использование столь малых по размеру КЭ в реальном проектировании не рекомендуется. Поэтому вынуждены принять A_S2=13,7 см²/м (шаг триангуляции 0,3 м). Как видим, адаптивная триангуляция занижает площадь арматуры.

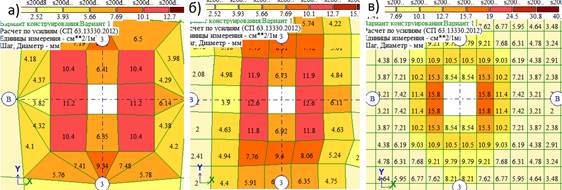
Рис. 7. Фрагменты схем с адаптивной триангуляцией при шаге:

а — равном 1,0 м; б — равном 0,4 м; в — равном 0,2 м В схемах с треугольной триангуляцией размеры отдельных КЭ могут отличаться от шага триангуляции на 20 — 63%. Во всех схемах с треугольной триангуляцией наблюдается эффект увеличения площади A_S2 по мере удаления центра тяжести КЭ от грани колонны (рис.8), что представляется не логичным. В схемах этой серии наблюдается самый большой разброс максимальных значений: от A_S2=10,03 до A_S2=20,49 см²/м (более 100%). Но, не все схемы можно признать корректными. Так, в образце с шагом триангуляции 1,0 м, центры тяжести ближайших к колонне КЭ расположены весьма далеко от ее грани, а именно на расстоянии от 0,2 до 0,38 м (A_S2=10,03 и A_S2=12,03 см²/м, соответственно), что является весьма грубой оценкой. В схеме с шагом триангуляции 0,2 м (рис. 8,в) у элементов, примыкающих к колонне, размер стороны мал: 0,11 — 0,13 м, что немногим больше половины толщины плиты. Во-первых, усилия, полученные в этих КЭ, описывают напряженное состояние локальной области, то есть представляют собой оценку концентрации напряжений в зоне сопряжения элементов. Во-вторых, применение столь малых размеров КЭ в реальных расчетах зданий и сооружений не рекомендуется.

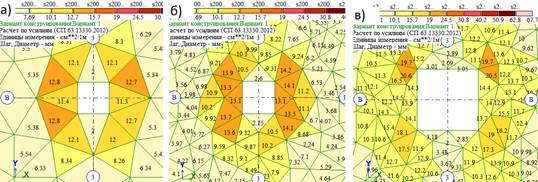
Рис. 8. Фрагменты схем с треугольной триангуляцией при шаге:

а — равном 0,6 м; б — равном 0,4 м; в — равном 0,2 м После исключения из рассмотрения этих схем при конструировании можно ориентироваться на оставшееся максимальное значение 17,3 см²/м (шаг 0,3 м), но в этом случае длина меньшей стороны КЭ составляет 0,2 — 0,25 м. Столь мелкая сетка лишает этот вариант практической ценности, поэтому принимаем A_S2=14,2 см²/м (шаг 0,4), см. таблицу № 1.

Таблица № 1

Площадь арматуры A_S2, рекомендуемая для конструирования.

Как видим, после отбраковки сомнительных результатов получено армирование почти одинаковое для всех способов генерации сетки. Очевидно, что оптимальным решением является вариант разбиения окрестности колонны на квадратные или близкие к квадрату прямоугольные конечные элементы, размеры которых совпадают с размерами поперечного сечения колонны без использования АЖТ.

• 1. Барабаш М. С., Палиенко О. И., Медведенко Д. В. Программный комплекс САПФИР — основа BIM-технологий. М.: АСВ, 2012. -356с.
• 2. ПК ЛИРА-САПР 2016. Проектирование и расчет строительных конструкций. [2016]. URL: liraland.ru/lira/.
• 3. Перельмутер А. В., Сливкер В. И. Расчетные модели сооружений и возможности их анализа. — М, 2007. — 595 с.
• 4. А. С. Городецкий, Л. Г. Батрак, Д. А. Городецкий, М. В. Лазнюк, С. В. Юсипенко. Расчет и проектирование конструкций высотных зданий из монолитного железобетона. — Киев, 2005. -106 с.
• 5. А. С. Городецкий, И.Д., Евзеров И. Д. Компьютерные модели конструкций. — Киев, 2004. — 344 с.
• 6. Мкртчян А. М., Аксенов В. Н. Отличия расчета колонн из высокопрочного бетона по нормам // Инженерный вестник Дона, 2013, № 4. URL: ivdon.ru/ru/magazine/archive/n4y2013/2131
• 7. Русаков А. И. Учет размера конечного элемента оболочки при расчете арматуры монолитных плит перекрытий // Промышленное и гражданское строительство. — 2011. — N 8. — С. 57−60.
• 8. Metin Husem, Selim Pul. Investigation of strain models for confined high strength concrete // «Sadhama» Vol. 32, Part 3, June 2007, pp 243−253. — India.
• 9. James K. Wight. Reinforced Concrete Mechanics and Design. 2009. -113p.
• 10. П. П. Польской, Д. Р. Маилян, С. В. Георгиев. О влиянии гибкости

стоек на эффективность композитного усиления // Инженерный вестник Дона, 2015, URL: ivdon.ru/ru/magazine/archive/n4y2013/2094.

References

• 1. Barabash M.S., Palienko O.I., Medvedenko D.V. Programmnyj kompleks SAPFIR — osnova BIM-tehnologij [A programmatic complex SAPPHIRE is basis of BIMof technologies].: M.: ASV, 2012. 356 p.
• 2. PK LIRA-SAPR 2016. Proektirovanie i raschet stroitel’nykh konstruktsiy [LIRA-SAPR 2016. Design and calculation of building structures]. URL: liraland.ru/lira/.
• 3. Perel’muter A.V., Slivker V.I. Raschetnye modeli sooruzhenij i vozmozhnosti ih analiza [Calculation models of building and possibility of their analysis.]. M, 2007. 595 p.
• 4. A.S. Gorodeckij, L.G. Batrak, D.A. Gorodeckij, M.V. Laznjuk, S.V. Jusipenko Raschet i proektirovanie konstrukcij vysotnyh zdanij iz monolitnogo ћelezobetona. [Calculation and design of construction of high-rise buildings made of reinforced concrete] Kiev, 2004. 106 p.
• 5. A.S. Gorodeckij, I.D., Evzerov I.D. Komp’juternye modeli konstrukcij [Computer models of constructions]. Kiev, 2004. 344 p.
• 6. Mkrtchjan A.M., Aksenov V.N. Inћenernyj vestnik Dona (RUS), 2013, № 4. URL: ivdon.ru/magazine/archive/n4y2013/2131
• 7. Rusakov A. I. Promyshlennoe i grazhdanskoe stroitel’stvo. 2011. N 8. pp. 57−60.
• 8. Metin Husem, Selim Pul. Investigation of strain models for confined high strength concrete. «Sadhama» Vol. 32, Part 3, June 2007, pp. 243−253. India.
• 9. James K. Wight. Reinforced Concrete Mechanics and Design. 2009. 113p.
• 10. P.P. Pol’skoj, D.R., Mailjan, S.V. Georgiev. Inћenernyj vestnik Dona (Rus), 2015, № 4. URL: ivdon.ru/ru/magazine/archive/n4y2015/3374