Модели прогнозирования в анализе маркетинговых процессов

Прогнозирование служит для выяснения тенденций развития фирмы в условиях постоянного изменения факторов внешней и внутренней среды и поиска рациональных маркетинговых мероприятий по поддержке устойчивости ее экономического поведения. Сфера применения методов прогнозирования в маркетинговых системах достаточно широка. Они используются для анализа и разработки концепций развития всех субъектов маркетинговой системы, например, для исследования рыночной конъюнктуры, в системе прогнозирования цен, новых продуктов и технологий, поведения покупателей на рынке. Важнейшим направлением является прогнозирование сбыта и рынков, их динамики, структуры, конъюнктуры, возможностей рынка воспроизводить предложение и спрос.

В качестве инструментария при прогнозировании используется система методов, с помощью которых анализируются причинноследственные параметры прошлых тенденций в деятельности предприятия и по результатам анализа формируются изменения в перспективе социально-экономического развития фирмы.

Существуют различные приемы и методы прогнозирования. Чаще других в прогнозировании спроса и предложения применяются:

• • аналоговые модели, когда в качестве прогноза рассматриваются благоприятные показатели рыночной ситуации в каком-либо регионе или стране;
• • имитационные, когда вместо реальных данных используются построения, созданные по специальной программе с помощью ЭВМ;
• • нормативные, или рационализированные, прогнозные расчеты, например проистекающие из рационального бюджета или рациональных рекомендуемых норм потребления (этот метод больше подходит для рынка средств производства, где большую роль играют производственно-технические нормативы и прочие детерминанты, чем для потребительского рынка, где потребности проявляются в форме статистических закономерностей);
• • прогнозирование по экспертным оценкам (обычно метод Дельфи);
• • методы экстраполяции: технические, механические способы сглаживания динамических рядов, трендовые модели;
• • методы статистического моделирования (парные и многофакторные уравнения регрессии);
• • прогнозирование по коэффициентам эластичности.

Процесс прогнозирования распадается на два этапа:

• 1) индуктивный — обобщение данных, наблюдаемых за достаточно продолжительный период, и представление статистических закономерностей в виде модели, которая выражается либо аналитической функцией тенденции развития, либо в виде зависимости от нескольких факторов-аргументов;
• 2) дедуктивный — собственно прогноз. На основе выявленных закономерностей определяют ожидаемые значения прогнозируемого показателя, которые должны быть критически осмысленны с содержательной точки зрения. Указанные этапы конкретизируются в определенной последовательности шагов.

Информационной базой для анализа прогноза являются динамические и временные ряды. Ряд динамики представляет собой числовые значения определенного статистического показателя, расположенные в хронологическом порядке. Числовые значения показателя, составляющего ряд динамики, называют уровнем. Тенденция (закономерность) в изменении уровней ряда называется трендом.

Рассмотрим методы прогнозирования товарного рынка в маркетинговых исследованиях.

Прогнозирование товарного рынка — это оценка перспектив развития рынка, изменения рыночных условий на предстоящий период для учета прогнозных данных в маркетинговых программах, в стратегии и тактике фирмы.

Прогнозирование рынка основывается на анализе фактических данных прошлого и настоящего исследуемого рынка. Цель прогноза — установить возможное проявление в перспективе факторов, воздействующих на рынок, включая общехозяйственную ситуацию, структурные сдвиги, динамику национального дохода, изменение факторов формирования цен и т. д. Знание перспектив развития того или иного рынка (сегмента рынка) крайне необходимо для действующей на этом рынке фирмы (либо собирающейся на него внедриться).

Товарное предложение, спрос и цены часто колеблются во времени с определенной периодичностью. Поэтому при анализе рынка весьма важно выявить и измерить степень таких колебаний, в частности колебаний сезонного характера.

1. Прогнозирование рынка путем экстраполяции его динамики. Нахождение неизвестного значения динамического ряда за его пределами путем механического переноса тенденций прошлого на будущее называется экстраполяцией. Экстраполяция — наиболее часто используемый и сравнительно простой метод прогнозирования. Для ее применения нужен минимум информации: всего один динамический ряд прогнозируемого показателя, как правило, за 5—7 периодов. Для прогнозирования может быть использована одна из трех разновидностей экстраполяции, причем выбор конкретного способа из этих трех зависит от характера имеющегося динамического ряда. Рассмотрим подробнее применение этих способов на конкретных примерах.

Расчет прогноза по среднему уровню ряда применяется тогда, когда динамический ряд не имеет тенденции роста или снижения и его колебания относительно невелики. В этом случае в качестве прогноза может быть использована средняя арифметическая показателей этого ряда.

Рассмотрим пример. Нужно спрогнозировать возможную продажу товара в торговой секции на седьмой день, если его продажа в предыдущие шесть дней характеризуется следующими данными:

Нетрудно заметить, что данный динамический ряд относительно стабилен и колеблется около средней величины. Расчет проводится по формуле простой средней арифметической:

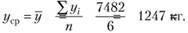
Полученную величину (1247 кг) можно прогнозировать как объем возможной продажи товара на седьмой день. Разумеется, фактическая продажа может несколько отличаться от нашего прогноза, но возможную среднюю ошибку прогноза рассчитывают по формуле.

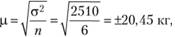
где? — средняя ошибка прогноза; ?2 — дисперсия ;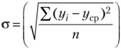

п — число показателей в динамическом ряду. Такое значение вполне приемлемо, поскольку при краткосрочном прогнозировании допускается средняя ошибка прогноза до 5%, а в нашем случае она составляет лишь 1,6% (20,45 / 1247 • 100).

2. Прогнозирование по средним темпам роста (снижения). Имеет смысл тогда, когда ряду динамики свойственна устойчивая тенденция к повышению или снижению. В этом случае предполагается, что каждый последующий член динамического ряда равен предыдущему, умноженному на средний коэффициент темпов роста (снижения) Iср. Коэффициент Iср исчисляется по формуле.

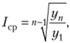
где уn — конечный показатель ряда; y1 — начальный показатель ряда; п — количество членов динамического ряда.

Затем на основе этого коэффициента можно вычислить прогнозируемый показатель на момент времени t по следующей формуле:

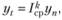
где 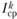— коэффициент прогнозируемого темпа роста (спада) на k (число прогнозируемых интервалов после интервала п).

Например, торговая организация обслуживает 100 тыс. жителей. Требуется рассчитать прогноз возможного объема продажи товара в седьмом году, если его продажа в расчете на одного человека за предыдущие пять лет характеризуется следующими данными:

Решение задачи будет иметь вид.

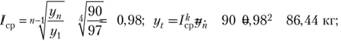
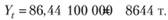
Таким образом, прогноз возможной продажи товара в седьмом году в расчете на одного человека составляет 86,44 кг, а в целом по торговой организации Y, = 8644 т.

3. Прогнозирование по скользящей средней. Сущность метода заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3, 5, 7 и т. д.), первых по счету уровней ряда, затем — из такого же числа уровней, но начиная со второго по счету, далее — начиная с третьего и т. д. Скользящие средние определим по формуле 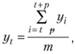когда т = (2р — 1) — нечетное число; при т = 3, р = 1, т. е. при t = 2у2 = (у1 + у2 + y3) / 3, при t = 3у3 = (у2 + у3 + y4) / 3 и т. д. Значение общего среднего уровня можно получить по следующей формуле:

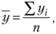
где п — количество значений выборки.

Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок. Скользящая средняя представляет собой сглаженный ряд и усредненную закономерность прогнозирования будущей деятельности. Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим. Индексы сезонности определяют по формуле.

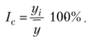
Рассмотрим пример расчета прогноза по скользящей средней. Фирма реализует товар. Данные годового объема продаж товара представлены в табл. 6.12.

Таблица 6.12

Исходные данные и результаты расчета продаж по скользящей средней

Месяц.	Объем продаж, тыс. руб.	Темп роста продаж к предшествующему периоду, %.	Трехмесячная скользящая средняя.	Индексы сезонности (/с). %.
Январь.		;	;	;
Февраль.		111,11.	(45 + 50 + 73) / 3 = = 56.	56 / 88,07 = = 64.
Март.		146,0.	(50 + 73 + 80) / 3 = = 67,67.
Апрель.		109,58.	(73 + 80 + 91)/3 = = 81,34.
Май.		113,75.	(80 + 91 + 130)/3 = = 100,3.
Июнь.		142,85.	(91 + 130+ 155)/3 = = 125,34.	100,65.
Июль.		119,23.	(130+ 155 + 100)/ /3= 128,34.
Август.		64,51.	(155 + 100 + 78)/ /3=111.
Сентябрь.		78,0.	(100 + 78 + 60)/3 = = 79,34.
Октябрь.		76,92.	(78 + 60 + 58) / 3 = = 65,34.
Ноябрь.		96,66.	(60 + 58 + 80) / 3 = = 66.
Декабрь.		138,93.	;	;
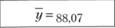				95,9.

Нужно найти средний объем продаж методом скользящей средней и оценить перепады в продажах через индекс сезонности. Составить график маркетинговых мероприятий по стимулированию продаж.

Прогнозный объем продаж на январь следующего года составит:

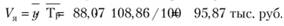
Совокупность исчисленных для каждого интервала времени индексов сезонности характеризует сезонную волну развития изучения явления в динамике. График сезонности (по месяцам) продаж чемоданов для примера из табл. 6.12 показан на рис. 6.4.

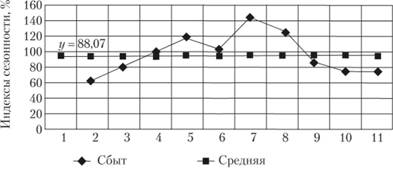
Рис. 6.4. Характеристика сезонной волны продаж на примере роликовых чемоданов.

Характеристика функции сбыта объясняется сезоном отдыха и путешествий. Исходя из характера диаграммы продаж (см. рис. 6.4) фирма выделяет три фазы проведения кампании по стимулированию: фаза 1 — с 15 февраля по 15 мая; фаза 2 — с 10 июня по 10 июля; фаза 3 — с 15 ноября по 31 декабря.

4. Прогнозирование на основе экспертных оценок. Экспертам было предложено спрогнозировать объемы продаж товара компании в следующем году. В распоряжении экспертов были данные о продажах товара компании и условия поставок, а также товаров конкурентов. По данным проведенного экспертного опроса о перспективах продаж товара компании составлена табл. 6.13.

Для определения оптимального количества групп с равными интервалами воспользуемся формулой Стэрджесса:

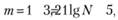
где N — число экспертов (30).

Таблица 6.13

Данные экспертного опроса о перспективности объема продаж товара компании в городе N

Ширина интервала.

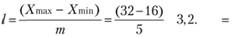
Результаты расчетов представлены в табл. 6.14.

Таблица в. 14

Результаты упорядочения вариационного ряда по опросам экспертов

Средняя величина прогнозируемого объема продаж определится по данным табл. 6.14:

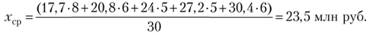
Рассчитаем характеристику ряда распределения прогнозов экспертов по объему продаж, для этого составим расчетную табл. 6.15.

Таблица в. 15

Вычисление элементов дисперсии

Величина объемов продаж, млн руб.	Количество экспертов. (f).	Середина интервала. (х)	xf	х2f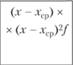
16−19,2.		17,7.	141,6.	2506,32.	49,12.
19,2−22,4.		20,8.	124,8.	2595,84.	13,74.
22,4−25,6.					1,25.
25,6−28,8.		27,2.		3699,2.	68,45.
28,8−32.		30,4.	182,2.	5544,96.	75,66.
		;	704,8.	17 226,32.	256,22.

Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она исчисляется по формуле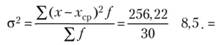

Среднее квадратическое отклонение равно корню квадратному из дисперсии. Для вариационного ряда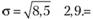

В соответствии с теоремой Чебышева 75% значений признака попадут в интервал 17,7—29,3 млн руб., а 89% всех значений — в интервал 14,8—32,2 млн руб.

5. Прогнозирование путем выравнивания (сглаживания) динамического ряда. Как правило, выравнивание по прямой используется в тех случаях, когда абсолютные приросты практически постоянны, т. е. когда уровни изменяются в арифметической прогрессии или близко к ней.

Простейшей моделью, выражающей тенденции развития, является линейная функция тренда. Рассмотрим построение линии тренда по прямой.

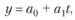
где a1 — коэффициент регрессии, определяющий направление развития тренда; t — порядковый номер периода или момента времени. Если а > 0, то уровни ряда динамики равномерно возрастают, а при а < 0 происходит их равномерное снижение.

Этому типу динамики присущи постоянные приросты: ?у = = const. Рассмотрим пример линейного прогноза развития продаж на основании данных табл. 6.16.

Таблица 6.16

Выравнивание по прямой объема продаж

Коэффициенты линейного уравнения тренда для нашего примера имеют следующий вид:

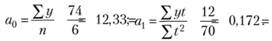
Коэффициент a1 характеризует уменьшение объема продаж на 0,172 млн руб. в месяц. Уравнение прямой, представляющее собой трендовую модель искомой функции (тенденции изменения объема месячных продаж), будет иметь вид.

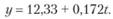
С помощью этой зависимости можно прогнозировать ситуацию в будущих периодах.

Вероятностные границы интервала прогнозируемого явления.

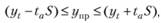
где ta — коэффициент доверия по распределению Стьюдента; S — остаточное среднеквадратическое отклонение от тренда;

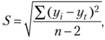
где п — количество интервалов.

На основании данных табл. 6.16, при доверительной вероятности 0,95 и уровне значимости 0,05, коэффициент доверия ta = 2306 (по таблице Стьюдента), тогда:

Продление в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции. По данным табл. 6.16 можно определить ожидаемый уровень продаж в июле месяце (исходя из уравнения у = 12,33 + 0,172t, при t = 7).

Зная точечную оценку прогнозируемого значения объема продаж на июль (Yиюль = 12,33 + 0,172 • 7 = 13,53), определим вероятностные границы интервала продаж: 13,53 — 2,306 • 2,39? yпр? 13,53 + + 2,306 • 2,39, или 8,018? yпр? 19,04. Следовательно, с вероятностью в 0,95 можно утверждать, что объем продаж в июле месяце будет не менее 8,018 млн руб., но и не более 19,04 млн руб.