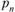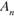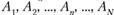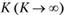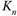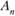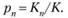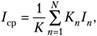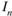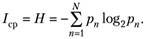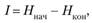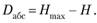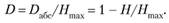Оценка количества информации для неравновозможных событий

Примером неравновозможных событий может служить частота появления одной из букв алфавита в тексте (книге, журнале), содержащем очень большое количество букв. Для русского алфавита буква «о» имеет наибольшую частоту появления 0,0940, «ъ» — наименьшую частоту появления 0,0002.

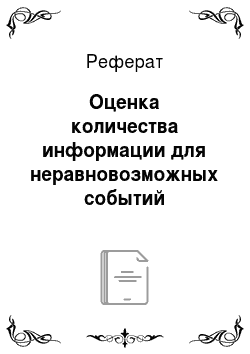
Вероятность 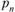появления события 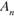, принадлежащего множеству 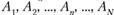неравновозможных событий, определяется на основании большого числа 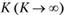проведенных испытаний как отношение числа 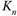появления события 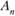к числу К всех испытаний.

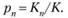(1.4).

Если в соотношение (1.3) подставить равенство (1.4), то получим выражение количества собственной, или индивидуальной, информации для неравновозможных событий.

Среднее количество информации для неравновозможных событий определяется выражением.

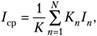(1.5).

где 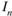- количество информации в n-м событии.

Подставив (1.3), (1.4) в (1.5), получаем известную в теории меру Шеннона.

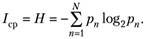(1.6).

Величину H называют энтропией, которая согласно выражению (1.6) соответствует количеству информации, приходящемуся на одно испытание, или степени неопределенности, снимаемой после проведения одного испытания. Из выражения (1.6) следует, что энтропия обладает следующими свойствами:

• • Я > О, так как рп< 1, поэтому log2 рп < 0;
• • Я = 0, когда одна из вероятностей рп = 1, а все остальные рп = 0 (событие достоверно) или все р = 0 (событие невозможно);
• • энтропия достигает максимального значения Я|Пах, когда все вероятности равны между собой, т. е. рп = 1 /N. При этом мера Шеннона (1.6) вырождается в меру Хартли (1.3). При N= 2 энтропия достигает абсолютного максимума тах =
• • энтропия двух независимых множеств А и В событий, образующих полное пространство, равна сумме энтропии исходных множеств (свойство аддитивности), Я = НА + Яд.

Выражение (1.6) для энтропии может быть использовано для оценки количества информации. В общем случае количество информации определяется степенью уменьшения энтропии в результате проведенного испытания, опыта или какого-либо другого акта познания. Количество информации /, содержащееся в сообщении, можно определить по формуле.

где Я||ач, Якон — начальная и конечная (до и после получения сообщения) энтропия (неопределенность).

Например, если после получения сообщения энтропия не изменилась, т. е. Якои = Я, то количество информации в полученном сообщении равно нулю (/= 0); если конечная энтропия Я = 0, то неопределенность снимается полностью и информация равна энтропии: 1= Н = Я||ач.

Избыточность информации

Полученные результаты позволяют определить абсолютную избыточность информации D.i (k как разность между максимально возможным количеством информации и энтропией.

Пользуются также понятием относительной избыточности информации