Метод анализа иерархий Т. Саати

Метод анализа иерархий был предложен в конце 1970;х гг. американским математиком Т. Саати^[1] [72]. Метод заключается в декомпозиции проблемы на более простые составляющие части и поэтапном установлении приоритетов оцениваемых компонент с использованием парных (попарных) сравнений.

На первом этапе выявляются наиболее важные элементы проблемы.

На втором — наилучший способ проверки наблюдений, испытания и оценки элементов.

На третьем — осуществляется выработка способа применения решения и оценка его качества.

Весь процесс подвергается проверке и переосмыслению, до тех пор пока не будет уверенности, что процесс охватил все важные характеристики, необходимые для представления и решения проблемы.

Процесс может быть проведен над последовательностью иерархий. При этом результаты, полученные в одной из них, используются в качестве входных данных при изучении следующей.

В наиболее простой иерархии, называемой Саати доминантной, он определяет три уровня: верхний уровень цели (или целей), средний — критерии, нижний — перечень альтернатив (рис. 6.1).

В структуре между целью и альтернативами может быть несколько промежуточных уровней (рис. 6.2). Например, уровень проблем, акторов (уровень действующих сил, в качестве которых могут выступать административные власти, жители и т. п.). Каждый из критериев может разделяться на субкритерии.

Иерархия считается полной, если каждый элемент заданного уровня функционирует как критерий для всех элементов нижележащего уровня. Иерархия может быть разделена на подиерархии.

Связи между уровнями часто изображают так, как показано на рис. 6.2.

Для реализации метода введен закон иерархической непрерывности, в соответствии с которым требуется, чтобы элементы каждого уровня были сравнимы по отношению к элементам вышестоящего уровня.

Между уровнями строятся матрицы. Для структуры, приведенной на рис. 6.1, матрицы строятся следующим образом: одна матрица для сравнения относительной важности критериев по отношению к цели и матрицы для оценки относительной значимости альтернатив относительно каждого из критериев второго уровня. Число матриц между уровнем критериев и альтернатив равно числу критериев. Общее число матриц равно числу критериев плюс одна для оценки критериев относительно цели.

Используемые в методе Саати попарные сравнения приводят к квадратным матрицам вида.

(6.2).

Эта матрица имеет свойство обратной симметрии, т. е.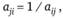

где индексы i и j относятся соответственно к строке и к столбцу. Обратные числа использованы в дальнейшем при обработке матрицы.

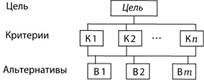
Рис. 6.1.

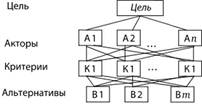
Рис. 6.2.

В матрицах элементы нижележащего уровня (альтернативы, варианты) сравниваются попарно по отношению к критериям, а критерии — по отношению к цели.

Эти оценки могут получаться различными способами. Но в методе Саати для оценки компонент рекомендуется специальная шкала от 1 до 9, в которой компонентам равной важности ставится в соответствие единица, при умеренном превосходстве — 3, при существенном превосходстве — 5, значительном превосходстве — 7 и очень сильном превосходстве — 9. Значения 2, 4,6, 8 используются как промежуточные между двумя соседними компонентами, получившими оценки 1, 3, 5, 7, 9 соответственно.

Относительная важность любого элемента, сравниваемого с самим собой, равна единице, т. е. диагональ матрицы состоит из единиц. При заполнении матрицы используется свойство обратной симметрии: симметричные клетки заполняются обратными величинами.

Получив совокупность матриц, можно принимать решение на основе их содержательного анализа, представив лицу, принимающему решения, оценки альтернатив по учитываемым критериям. Однако желательно получить обобщенные оценки альтернатив. Для этого можно применить различные способы усреднения. Саати предлагает использовать среднегеометрическое усреднение и нормирование полученных обобщенных оценок. Пример такой процедуры приведен в табл. 6.1.

Поскольку при такой, достаточно сложной, процедуре обработки оценок неизбежны приближенные вычисления корней (особенно при большом числе критериев), то для проверки согласованности полученных результатов предлагается умножить матрицу на нормированные оценки и получить меру оценки степени отклонения от согласованных оценок — индексы согласованности для каждой из матриц и иерархии в целом:

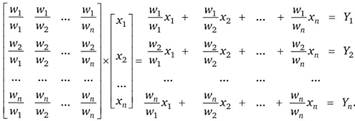(6.3).

Таблица 6.1.

	Матрица.	Вычисление оценок компонент собственного вектора по строкам.	Суммирование элементов столбцов и нормирование.	Нормирование результатов для получения оценок вектора приоритетов.
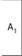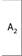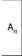		Сумма.

Возможность и целесообразность такой оценки базируется на том, что при рассмотренной выше процедуре 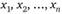есть не что иное, как 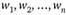соответственно. Однако приближенные вычисления могут привести к рассогласованию оценок.

Важно также отметить, что в матрице суждений нет дробных отношений, есть только целые числа или их обратные величины.

После получения индексов согласованности их сравнивают с допустимыми (отклонение 10% и менее). Если необходимой согласованности не получится, процедуру оценки нужно повторить.

С конкретными примерами расчетов можно познакомиться в работе Г. Саати и К. Кернса «Аналитическое планирование: Организация систем» [72, с. 33−43].

При применении метода следует иметь в виду, что, как отмечает Саати, «сложная математика не может „улучшить“ то, что индивидуум не хочет менять» [72, с. 37]. Если требуемая согласованность не получена, следует возвратиться к опросу, изменяя формулировки вопросов, а при необходимости и критерии. Оговаривает Саати также целесообразность учета гипотезы Миллера: оценивать не более 7+2 составляющих на каждом уровне.

• [1] Saaty, Т. L. The Analytic Hierarchy Process / T. L. Saaty. — New York: McGraw-Hill International, 1980.