Моделирование антагонистических взаимодействий

Взаимодействие двух индивидов называют антагонистическим, если они преследуют прямо противоположные цели. Предполагается, что каждый индивид стремится максимизировать некоторый целевой показатель, причем оба эти показателя имеют одинаковое экономическое содержание и выражаются в одних и тех же единицах измерения. Обычно в роли такого универсального измерителя выступают деньги. Антагонистический характер взаимодействия выражается в том, что увеличение целевого показателя одного индивида неизменно вызывает равное по величине уменьшение целевого показателя другого индивида. Иными словами, арифметическая сумма целевых показателей остается неизменной при любых действиях индивидов. Обычно полагают, что эта сумма равна нулю. Тогда если целевой показатель одного индивида положителен (выигрыш), то для другого он отрицателен (проигрыш), и наоборот.

Игровая модель антагонистического взаимодействия является частным случаем обшей игровой модели межчеловеческих взаимодействий и называется игрой с нулевой суммой. Матрица выигрышей (или игровая матрица) в данном случае состоит из пар, равных по модулю и противоположных по знаку чисел, что позволяет записать ее в более простой форме, содержащей только выигрыши первого игрока. Такая матрица называется платежной.

В табл. 3.12 приведен пример платежной матрицы. Предположим, что первый игрок выбрал первый вариант поведения, а второй игрок — третий вариант поведения. Тогда данному ходу игроков отвечает элемент платежной матрицы, равный -1. Это значит, что первый игрок проигрывает одну денежную единицу, а второй игрок выигрывает ее. Поэтому результат описанного единичного взаимодействия трактуют как передачу одной денежной единицы от первого игрока второму игроку.

Таблица 3.12

Платежная матрица и осторожные стратегии.

Рассмотрим несолидарные стратегии поведения игроков в игре с нулевой суммой.

1. Нерациональное поведение. Доминирующая стратегия первого игрока в данной игре определяется так же, как в общем случае. Для второго игрока доминирующей является та из двух стратегий, у которой соответствующие элементы столбца платежной матрицы меньше, чем элементы другого столбца. Стратегия второго игрока, для которой существует доминирующая стратегия, является нерациональной.

Пример I. В табл. 3.12 представлена платежная матрица. Ее вторая строка является доминирующей по отношению к первой строке, поэтому первый вариант поведения первого игрока нерационален. У второго игрока нерациональных стратегий нет.

2. Осторожное поведение. Осторожная стратегия первого игрока определяется так же, как в общем случае. Осторожная стратегия второго игрока определяется следующим образом. В каждом столбце платежной матрицы находят максимальный элемент. Затем из этих максимальных значений выделяют минимальное. Это число называется минимаксом. Если минимакс положителен, то он равен максимальной величине возможного проигрыша второго игрока независимо от поведения первого. Если минимакс отрицателен, то он равен минимальному гарантированному выигрышу второго игрока независимо от поведения первого.

Пример 2. В табл. 3.12 показан алгоритм поиска осторожных стратегий игроков. Максимин равен единице, а осторожная стратегия первого игрока отвечает второму варианту поведения. Минимакс также равен единице, а второй вариант поведения также является осторожным для второго игрока. Осторожные стратегии игроков обозначены в таблице звездочками.

3. Оптимизирующее поведение. Равновесной точкой платежной матрицы называют ее элемент, который является минимальным в своей строке и максимальным в своем столбце. Такой элемент известен также как седловая тонка платежной матрицы или седловой элемент. Стратегии игроков, отвечающие седловой точке, называют равновесными. Платежная матрица может иметь несколько седловых точек, а может и не иметь их вовсе. Напомним, что здесь рассматриваются только чистые стратегии.

Главное свойство седлового элемента платежной матрицы состоит в том, что он равен одновременно максимину и минимаксу. Отсюда следует ряд выводов:

• а) в случае антагонистических взаимодействий равновесные стратегии являются также осторожными;
• б) если игроки следуют равновесным стратегиям, то седловой элемент равен денежной сумме, которую передает один игрок другому за один ход. Если седловой элемент положителен, то платит второй игрок, а если отрицателен, то платит первый;
• в) если седловой элемент игровой матрицы положителен, то игра изначально «настроена» в пользу первого игрока. Если же седловой элемент отрицателен, то игра «настроена» в пользу второго игрока. Если седловой элемент равен нулю, то игра считается «справедливой»;
• г) если игровая матрица имеет несколько седловых элементов, то все они равны между собой. Поскольку равновесные точки равноценны для игроков, у последних не возникает стимула переходить из одного равновесного состояния в другое.

Пример 3. В платежной матрице, представленной в табл. 3.12, седловой элемент расположен на пересечении второй строки и второго столбца. Таким образом, данная игра «настроена» в пользу первого игрока. Равновесные стратегии игроков обозначены в таблице звездочками.

4. Отгоняющееся поведение. Выбор игроком неравновесного варианта приведет к уменьшению его выигрыша (или увеличению проигрыша) в случае, когда другой игрок сохраняет верность равновесной стратегии.

Пример 4. Второй вариант поведения является равновесным для обоих игроков (табл. 3.12). Предполагается, что второй игрок неизменно следует равновесной стратегии. Если первый игрок выберет первый вариант поведения, то его выигрыш уменьшится с единицы до нуля, а если третий вариант — он уменьшится до -2.

5. Инновационное поведение в случае антагонистических взаимодействий не имеет смысла, поскольку все седловые точки платежной матрицы равноценны для игроков.

Механизм согласования стратегий поведения игроков в общей модели межчеловеческих взаимодействий был основан на существовании неких комбинаций вариантов поведения, способствующих увеличению выигрышей обоих игроков. Но в случае антагонистических взаимодействий увеличение выигрыша одного игрока неминуемо влечет за собой сокращение выигрыша другого, поэтому согласованное поведение игроков невозможно. Таким образом, игровые модели антагонистических взаимодействий описывают скорее поведение «экономического человека», нежели «институционального человека».

Пример 5 (игра «Реклама»). Рассматривается ситуация, когда на рынке некоторого товара конкурируют две фирмы: известная и неизвестная. Каждая фирма имеет два варианта поведения: рекламировать свой товар или не рекламировать его. Рынок товара насыщен, поэтому рекламирование приводит не к увеличению суммарной прибыли фирм, а к ее перераспределению между ними. Если обе фирмы рекламируют товар, их прибыли остаются на прежнем уровне, т. е. перераспределение прибылей не происходит. Этот факт отражается нулевым элементом платежной матрицы. Если обе фирмы не рекламируют товар, то покупатели не получают никакой информации о неизвестной фирме и по привычке предпочитают товар известной фирмы, которая в итоге увеличивает свою прибыль на единицу. Если известная фирма не рекламирует товар, а неизвестная рекламирует, то последняя увеличивает число своих постоянных покупателей, а ее прибыль при этом увеличивается на единицу. И наконец, если известная фирма рекламирует товар, а неизвестная не рекламирует, то известная фирма получает максимальный прирост прибыли, равный 2. Понятно, что при этом прибыль неизвестной фирмы уменьшается на ту же величину. Платежная матрица игры представлена в табл. 3.13.

Рассмотрим возможные стратегии поведения конкурирующих фирм.

Игра «Реклама.

Во-первых, стратегия «Не рекламировать» является нерациональной для каждой фирмы, поскольку доминирующей для нее служит стратегия «Рекламировать».

Во-вторых, стратегия «Рекламировать» является осторожной для каждой фирмы, при этом максимин и минимакс равны нулю.

В-третьих, стратегия «Рекламировать» является равновесной стратегией для каждой фирмы. Поскольку седловой элемент платежной матрицы равен нулю, игра является «справедливой».

Таким образом, у фирм есть единственный разумный способ поведения — рекламировать товар.

Пример 6(Игра «Таможня»). Рассматривается ситуация, когда на таможне производится проверка правильности оформления груза. Таможня может проверить груз, а может и не делать этого. Перевозчик также имеет два варианта поведения: оформить груз правильно или оформить его неправильно. При правильном оформлении сумма таможенных сборов больше чем при неправильном (3 против 2 тыс. долл.). Если в ходе проверки таможня установила, что груз оформлен неправильно, то она взыскивает с перевозчика штраф в размере 4 тыс. долл. Если проверка груза показала, что он оформлен правильно, то таможня вынуждена выплатить перевозчику денежную компенсацию в размере 1 тыс. долл, за задержку транспортного средства и понесенные убытки. Платежная матрица игры представлена в табл. 3.14.

Рассмотрим возможные стратегии поведения таможни и перевозчика.

Во-первых, игроки не имеют нерациональных стратегий, поскольку ни одна стратегия нс является доминирующей.

Во-вторых, стратегия «Не проверить» является осторожной для таможни, она уберегает ее от возможной выплаты компенсации перевозчику. Максимин равен 2 тыс. долл. — гарантированный доход таможни. Стратегия «Правильно оформить» является осторожной для перевозчика, она уберегает его от возможного штрафа. Минимакс равен 3 тыс. долл. — максимальные возможные потери перевозчика.

Игра «Таможня».

В-третьих, в данной игре нет седловой точки, т. е. отсутствуют чистые равновесные стратегии игроков. Чтобы исследовать оптимизирующее поведение игроков в игре без седловой точки, необходимо отказаться от ограничивающего предположения, что игроки реализуют только чистые стратегии, т. е. неизменно выбирают один вариант поведения на протяжении рассматриваемого периода времени. Ниже под термином «стратегия» может пониматься как чистая, так и смешанная стратегия.

Покажем на примере рассматриваемой игры алгоритм вычисления смешанных равновесных стратегии игроков. Для этого введем важное определение. Цена игры есть математическое ожидание выигрыша первого игрока в случае, когда оба игрока придерживаются равновесных стратегий. Цену игры обозначим через V. Обозначим через р равновесную вероятность (частоту) проверки груза таможней, тогда равновесная стратегия таможни выражается вектором (р, 1 -р). Обозначим через q равновесную вероятность (частоту) правильного оформления документов перевозчиком. Тогда его равновесная стратегия выражается вектором (q, 1 -q). Запишем равновесные стратегии игроков в табл. 3.14.

Рассчитаем количественные параметры равновесной стратегии таможни. В случае, когда перевозчик следует неравновесной чистой стратегии «Правильно оформить», а таможня следует своей равновесной стратегии, то ее средний выигрыш составит.

Если перевозчик следует неравновесной чистой стратегии «Неправильно оформить», а таможня следует своей равновесной стратегии, то ее средний выигрыш составит.

Если перевозчик следует некоторой неравновесной стратегии, то выражения (3.1) и (3.2) больше цены игры, т. е. перевозчик теряет больше, чем в ситуации равновесия. Если же перевозчик следует своей равновесной стратегии, то данные выражения равны цене игры. Приравнивая каждое из равенств (3.1) и (3.2) к цене игры, получим систему двух уравнений с двумя неизвестными. Ее решение:

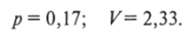
Таким образом, равновесная стратегия таможни состоит в том, чтобы проверять 17% грузов, или каждый шестой груз. Если оба игрока следуют своим равновесным стратегиям, то таможня получает в среднем 2,33 тыс. долл, с одного перевозчика.

Сделаем два замечания относительно полученного значения цены игры. Во-первых, этот показатель положителен, т. е., как и следовало ожидать, игра изначально «настроена» в пользу таможни. Во-вторых, цена игры больше максимина и меньше минимакса. Это соотношение справедливо для любой игры с нулевой суммой.

Рассчитаем параметры равновесной стратегии перевозчика. Если таможня проверяет все грузы, а перевозчик следует равновесной стратегии, то его ожидаемые потери составят.

Если таможня следует своей равновесной стратегии, то выражение (3.3) равно цене игры. Приравнивая это выражение полученному ранее значению цены игры, получим уравнение, его решение q= 0,33. Таким образом, равновесная стратегия перевозчика заключается в том, чтобы правильно оформлять груз лишь в 33% случаях.

В табл. 3.15 представлены возможные первые 12 ходов игры «Таможня». Как следует из таблицы, при реализации равновесных стратегий каждый игрок случайным образом чередует варианты поведения с частотой, задаваемой равновесной стратегией. Таможня проверила груз лишь два раза (3-й и 11-й ходы) из 12 возможных, т. е. в 17% случаев. Перевозчик, в свою очередь, правильно оформил документы 4 раза (1-й, 3-й, 7-й и 10-й ходы), т. е. в 33% случаев. Средний выигрыш таможни за.

Таблица 3.15

Смешанные равновесные стратегии.

12 ходов составил 2,17, что несколько меньше цены игры. Чем больше ходов будет сделано игроками, реализующими равновесные стратегии, тем ближе к цене игры будет величина среднего выигрыша таможни.