Кривые в пространстве

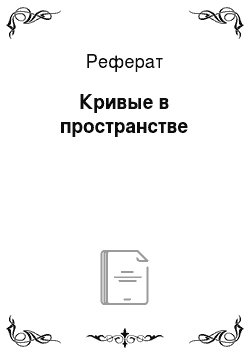
Начнем рассмотрение геометрического моделирования со способов задания кривых в пространстве. В простейшем случае кривая в трехмерном пространстве задается с помощью следующего параметрического представления:

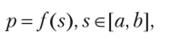
где s — вещественный параметр, принимающий значения из заданного отрезка [а, Ь]. Часто в качестве отрезка рассматривают отрезок [0, 1].

Производная функции / задает в каждой точке кривой (в которой она существует) касательный вектор к кривой. С помощью этого касательного вектора можно найти длину кривой, используя для этого формулу.

Поверхности в пространстве

Одним из простейших способов задания геометрической модели является явное (или параметрическое) задание, когда мы описываем поверхность модели с помощью некоторой функции. В общем виде поверхность может быть задана явно уравнением.

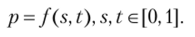
Таким образом можно описать широкий класс различных поверхностей. Введя сетку на [О, I]², можно перейти от явного представления поверхности к представлению в виде набора треугольников (полигональному представлению).

Если в этом представлении мы зафиксируем один из параметров, например, положим t = t₀, то получим кривую в пространстве, задаваемую уравнением р — f (s, t₀). Используя эту кривую, можно легко получить касательный вектор к поверхности в произвольной точке (s₀, t₀); он будет равен //(s₀,?₀). Аналогично можно зафиксировать другой параметр — s = s₀ — и найти второй касательный вектор в точке //(s₀,?₀) (рис. 6.1).

Рис. 6.1. Касательные векторы к поверхности в точке.

Таким образом, в произвольной точке нетрудно найти два касательных вектора и, зная их, определить единичный вектор нормали в точке через векторное произведение касательных векторов:

Параметрическое представление очень удобно для задания набора стандартных объектов, таких как прямоугольные параллелепипеды, сферы, цилиндры и т. п. Однако далеко не всегда можно найти достаточно простое параметрическое представление. Так, сферу в пространстве можно задать в сферических координатах, являющихся обобщениями полярных координат в трехмерном пространстве:

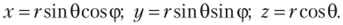
Отметим, что параметрическое представление поверхности — далеко не единственное: если есть одно представление, то всегда существует и другое.

В ряде случаев удобнее использовать неявный способ задания геометрии. При таком подходе поверхность задается уравнением.

Данное уравнение задает некую поверхность в трехмерном пространстве.

Часто встречается случай, когда значения функции F меньше нуля внутри тела, ограниченного поверхностью, и больше нуля вне этого тела. Так, сферу в трехмерном пространстве с центром в точке (лг₀, уц, 2₀) и радиусом г можно задать с помощью следующего уравнения:

При этом точкам внутри сферы будут соответствовать отрицательные значения, а точкам вне ее — положительные.

Подобное представление позволяет строить сложные поверхности. Для неявного представления можно легко найти значения нормали в произвольной точке — для этого достаточно вспомнить, что градиент такой функции определяет направление скорейшего возрастания функции. Таким образом, нормаль — это просто нормированный градиент:

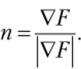
Неявное представление можно рассматривать как частный случай объемного представления: для каждой точки пространства задается некоторое значение, и интересующая нас поверхность является поверхностью уровня, т. е. множеством точек, где это значение равно некоторой заданной величине. Когда значения заданы на сетке, говорят о вокселах — обобщении пикселов на трехмерный случай.

Довольно часто данные для объемного представления берутся в результате каких-либо процедур: например, использование компьютерной томографии дает набор значений в пространстве на заданной сетке (вокселов).

Существует стандартная процедура перехода от объемного представления к полигональному, строящая фактически поверхность уровня в пространстве. При этом все пространство разбивается на элементарные кубики. Вершинами их являются точки сетки, в которых заданы значения. Далее для каждого такого кубика, исходя из значений в его восьми вершинах, строится набор треугольников, являющихся приближением поверхности уровня. Подобный алгоритм называют алгоритмом шагающих кубиков (marching cubes).

Если рассмотреть отдельный кубик и сравнить значения в его вершинах с заданным пороговым значением, можно увидеть, что общее число возможных вариантов — 256. Однако за счет использования симметрии можно сократить это число до совсем небольшого количества вариантов, показанных на рис. 6.2.

После определения конфигурации, исходя из значений в вершинах кубика, путем линейной интерполяции находят точки пересечения поверхности уровня с ребрами кубика и через них проводят треугольники. Код для подобной триангуляции в книге нс приводится, основная часть этого кода состоит из таблиц, определяющих, как для заданной конфигурации нужно строить треугольники. Хорошую реализацию этого алгоритма можно найти в интернете по адресу http://paulbourke.net/geometry/polygonise/.

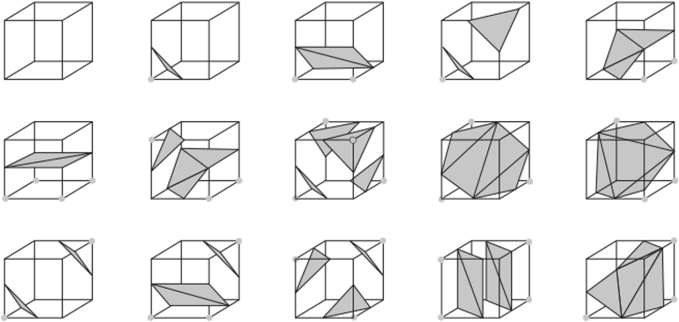
Рис. 6.2. Возможные варианты прохождения поверхности уровня через элементарный кубик.

Вместо шагающих кубиков можно также рассматривать шагающие тетраэдры — преимуществом такого подхода является заметно меньшее число возникающих вариантов.

Обычно вексельное представление занимает очень много места (по сравнению с полигональным представлением), поэтому часто используется следующий подход для сжатия этих данных — разреженные вексельные деревья (Sparse Voxel Octrees, SVO). При таком подходе в области пространства, где заданы данные, строится восьмеричное дерево. Начинают с прямоугольного параллелепипеда, содержащего внутри себя все заданные точки. Далее этот параллелепипед разбивают на восемь равных частей (рис 6.3).

Рис. 6.3. Разбиение параллелепипеда для построения разреженного воксельного дерева.

Каждая из частей этого параллелепипеда также является прямоугольным параллелепипедом. Далее находят минимальное и максимальное значения внутри этого параллелепипеда. Если разница между ними больше заданной точности и размер параллелепипеда больше заданного, то опять разбивают параллелепипед на части. Этот процесс разбиения повторяется необходимое число раз. В результате получают восьмеричное дерево в пространстве. При этом в тех областях пространства, где значение почти не изменяется, разбиения почти не будет. Таким образом, дерево оказывается разреженным — его разбивают только там, где э го необходимо.

Распространенным случаем неявного задания является использование функции расстояния со знаком (signed distance field, SDF) — в этом случае в качестве значения функции в точке выступает кратчайшее расстояние до поверхности, взятое со знаком плюс, если точка лежит вне поверхности, и минус — если точка лежит внутри. Рассмотренная выше функция, задающая сферу, является именно такой функцией.

Помимо сферы можно построить функции расстояния для целого ряда примитивов. Если у нас есть фигура, представляющая собой результат логической операции объединения, пересечения или вычитания двух других поверхностей, заданный с помощью функций расстояния, то мы можем легко построить функцию расстояния для итоговой фигуры.

Пусть у нас есть объект Л, заданный функцией расстояния d_A(p) и объект В, заданный функцией расстояния d_B(j)). Тогда функция расстояния для объединения фигур А и В будет равна min (d_A(p), d_B(p)).

Пересечению этих двух объектов будет соответствовать функция расстояния таx (d_A(p), d_B(p)). Разности соответствует функция расстояния таx (-d_A(p), d_B(p)).

Если для пересечения объектов нужно получить «сглаженное» пересечение, то вместо функции min можно использовать функцию.

Еще одним способом задания сложных геометрических моделей может быть использование стандартных операций над множествами — объединения, пересечения и вычитания — над более простыми объектами.

Данный подход называется конструктивной блочной геометрией (Constructive Solid Geometry, CSG) и позволяет строить сложные объекты с помощью операций объединения, пересечения и вычитания над элементарными объектами. При этом каждый такой сложный объект может быть представлен бинарным деревом, где узлам соответствуют операции над множествами, а листьям — элементарные геометрические объекты.

Использование функций расстояния и воксельного представления позволяет легко реализовать подобные операции. Однако для явного (параметрического) и полигонального представлений применение подобных операций является довольно сложным.

Очень часто при моделировании объектов применяют различные поверхности. Ниже рассмотрим некоторые распространенные случаи. Одним из них является задача, когда есть некоторая кривая и нужно построить поверхность, используя эту кривую.

Самыми распространенными случаями являются вытягивание (lofting) и построение поверхностей вращения (рис. 6.4). В случае вытягивания кривой у нас есть параметрически (или явно) заданная кривая р = f (t), t е [0,1] и направление /, в котором мы хотим вытягивать. Тогда можно параметрически описать поверхность следующим образом:

Соответственно, в качестве касательных векторов в произвольной точке (.v₀, /:₀) выступают векторы/'(/₀) ^и I^а нормалью к поверхности будет их векторное произведение.

Рис. 6.4. Вытягивание кривой.

В случае построения поверхности вращения (рис. 6.5), зная уравнение кривой, также можно без труда построить параметрическое представление поверхности вращения.

Пусть есть плоская кривая, заданная следующими уравнениями на плоскости:

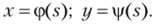
Тогда в результате вращения этой кривой вокруг оси Oz получаем поверхность, заданную уравнениями.

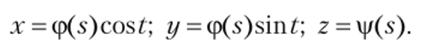
Из этих уравнений можно найти касательные векторы и вектор нормали к поверхности вращения.

Рис. 6.5. Поверхность вращения.

Довольно часто для построения сложных поверхностей и кривых используют кривые и поверхности Безье, а также различные сплайны. Сначала рассмотрим кривые Безье и Эрмита, а затем перейдем к поверхностям и сплайнам.

Кривая Безье задается своим набором контрольных точек Р₀,…, Р_т. Число т называется порядком кривой. Зная контрольные точки кривой, можно задать ее параметрически следующим образом:

Через В^от(t) обозначены многочлены Бернштейна, которые задаются формулой.

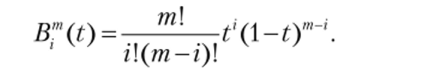
На рис. 6.6 приведены графики многочленов Бернштейна третьей степени. Многочлены Бернштейна обладают следующими свойствами:

• • они принимают неотрицательные значения на отрезке [0, 1 ];
• • сумма всех многочленов Бернштейна заданной степени тождественно равна единице;
• • порядок многочлена равен т.

Из уравнения кривой Безье и свойств многочленов Бернштейна можно записать уравнение касательной к этой кривой:

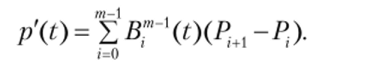
Рис. 6.6. Многочлены Бернштейна третьей степени.

Кривая Безье обладает рядом важных свойств:

• • она гладкая;
• • начинается в точке Р₀ и заканчивается в точке Р_т;
• • полностью содержится в выпуклой оболочке своих контрольных точек;
• • симметрична — если переставить контрольные точки в противоположном порядке, то получится та же самая кривая;
• • в начале кривая касается отрезка PqP^ а в конце — отрезка Р Р •
• 1 ^{т-Iх т >}
• • если все контрольные точки кривой лежат на одной прямой, то и соответствующая кривая Безье полностью лежит в этой прямой;
• • если все контрольные точки лежат на некоторой плоскости, то и вся кривая Безье также целиком лежит на этой плоскости.

Одним из наиболее часто встречающихся типов кривой Безье является кубическая кривая Безье (кривая Безье третьего порядка) (рис. 6.7).

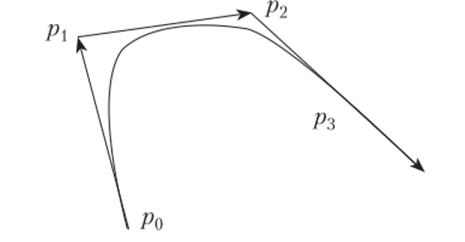
Рис. 6.7. Кривая Безье третьего порядка.

Если у нас много входных точек, то построение одной кривой Безье по ним будет не самым удачным решением — получается очень высокий порядок кривой. Более удачное решение — построение составной кривой Безье — кривой, состоящей из нескольких отдельных кривых Безье невысокого порядка. Однако в этом случае необходимо наложить дополнительные условия на контрольные точки, чтобы получившаяся составная кривая Безье была непрерывной и гладкой.

Чаще всего такая составная кривая Безье строится из отдельных кривых Безье третьего порядка (рис. 6.8). Для того чтобы гарантировать непрерывность производных первого порядка, необходимо, чтобы любые три точки вида P_{3i v}P_3j, P_3M лежали на одной прямой.

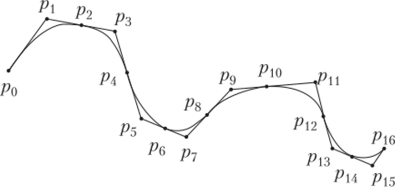
Рис. 6.8. Составная кривая Безье третьего порядка

Еще одним часто встречающимся классом кривых являются кривые Эрмита. Далее рассмотрим кривые Эрмита третьего порядка. Если у нас есть две точки Р_{) и Р_ь а также два вектора <2о и <2], то мы можем построить кривую Эрмита третьего порядка следующим образом:

Кроме кривой Безье есть также и поверхность Безье. Если имеется двухмерный массив точек Р, г = 0, m, j = 0, n, то можно построить параметрическую поверхность:

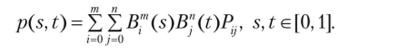
Частным случаем поверхности Безье является бикубическая поверхность Безье, соответствующая случаю п = т = 3.

Как и кривая Безье, поверхность Безье обладает некоторыми довольно полезными свойствами:

• • она гладкая;
• • ограничена четырьмя кривыми Безье соответствующего порядка (p (s, 0), p (s, 1), р (0, t), p{ 1, t));
• • полностью лежит в выпуклой оболочке своих контрольных точек;
• • если все контрольные точки лежат на некоторой плоскости, то и вся поверхность Безье также будет лежать на этой плоскости.

Аналогичным образом можно определить и поверхность Эрмита.

Одной из часто встречающихся задач является задача интерполяции: имеется некоторый набор точек и необходимо провести гладкую кривую через эти точки (рис. 6.9). При этом могут быть какие-то ограничения на класс используемых кривых, чаще всего рассматриваются кривые, заданные с помощью многочленов.

В двухмерном случае задачу часто ставят следующим образом: есть набор узлов a=t_Q { <…m — h и каждому узлу поставлено в соответствие значение у_{. Цель — построить функцию s (t)_y такую, что s (t_j) = y_r

Рис. 6.9. Интерполяция.

Естественным классом для подобных функций являются многочлены заданной степени. Известно, что для этой задачи всегда существует многочлен степени т (и притом единственный), называемый интерполяционным многочленом Лагранжа. Его можно задать следующим образом:

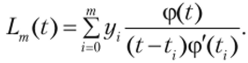
Здесь функция (р (?) задается следующим образом:

Однако использование интерполяционного многочлена Лагранжа часто бывает неудобным, но следующим причинам:

• • порядок многочлена зависит от числа точек и может быть очень высок;
• • изменение любой из точек ведет к изменению всего многочлена;
• • добавление новой точки увеличивает степень многочлена и приводит к необходимости его полной перестройки.

Поэтому довольно часто для интерполяции используют так называемые сплайны. Сам термин изначально обозначал гибкую металлическую линейку, которую пропускали через заданные точки и получали в результате гладкую кривую.

Функция s (t) называется сплайном, если:

• • на каждом частичном отрезке [?.,?.₊₁] эта функция является многочленом степени р
• • она имеет непрерывные производные вплоть до порядка р — 1 на всем отрезке.

Многочлен степени р задается с помощью р + 1 коэффициента. Поэтому, если у нас есть т + 1 узлов, то нам нужно т (р + 1) коэффициентов, для того чтобы однозначно определить сплайн.

Из условия непрерывности производных получаем условия на коэффициенты: во всех внутренних узлах должны совпадать производные справа и слева вплоть до порядка р — 1. Также мы получаем условия из требования прохождения сплайна через заданные точки. Несложно убедиться в том, что нам не хватает всего р — 1 условия, для того чтобы однозначно определить все требуемые коэффициенты. Обычно эти условия задаются в точках ?₀ и t_m и называются граничными условиями. Таким образом, для любого набора заданных точек можно построить сплайн, проходящий через точки этого набора.

Другим способом построения кривой, проходящей через заданные точки, является использование Б-сплайнов (рис. 6.10).

Б-силайн заданной степени п определяется уравнениями Кокса — де Бура.

В случае, когда расстояние между соседними узлами постоянно, соответствующий Б-сплайн называется однородными.

Если есть набор контрольных точек P₀,…, P_m__{n V} то можно определить Б-сплайновую кривую следующим образом:

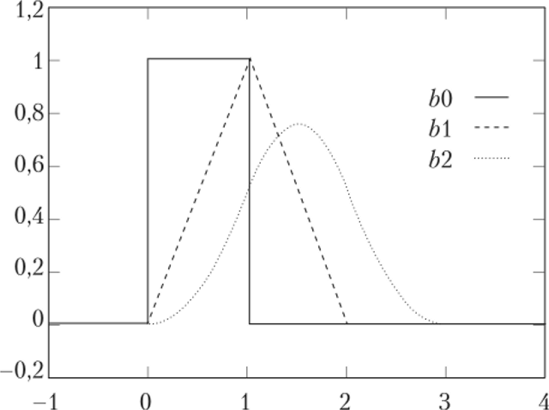
Рис. 6.10. Б-сплайны третьего порядка.

Для однородных кубических Б-сплайнов получаем.

Функции b_in(t), используемые для построения Б-сплайновой кривой, удовлетворяют ряду свойств:

• • они неотрицательны;
• • их сумма равна единице;
• • вне некоторого интервала каждая из них равна нулю.

Фактически Б-сплайны определяются как взвешенная сумма контрольных точек, причем веса определяются коэффициентами b_in(t). При этом каждая контрольная точка влияет не на всю кривую, а только на небольшой ее участок. Но иногда оказывается желательным дать некоторым контрольным точкам больший или меньший вес по сравнению с другими контрольными точками. При этом, если мы предположим, что для каждой точки есть свой вес w_jy то мы потерям свойства, когда сумма всех весов всегда равна единице (если раньше в качестве весов выступали Б-сплайны, то теперь Б-сплайны, умноженные на Wj). Для того чтобы сохранить это свойство, необходимо произвести нормализацию весовых функций:

В качестве весовых функций выступают следующие функции:

Обратите внимание, что сумма весовых функций опять равна единице.

Подобная кривая называется неоднородным рациональным Б-сплайном, или NURBS (Non-Uniform Rational В-Spline).

Существует довольно простая геометрическая интерпретация NURBS: если объединить трехмерные координаты контрольной точки с ее весом w_v то получится вектор в однородных координатах. Тогда на этих четырехмерных векторах можно построить Б-сплайн и после перехода от однородных координат к обычным трехмерным координатам получить NURBS.

Сплайны позволяют задавать довольно сложную геометрию с помощью небольшого числа контрольных точек. Для изменения полученных моделей достаточно просто передвинуть одну или несколько контрольных точек.

Большинство современных систем трехмерного моделирования поддерживают работу с различными сплайновыми поверхностями.