Марковские модели надежности, основные положения

Марковские процессы являются одним из аффективных инструментов анализа надежности, применяемым для оценки вероятностных характеристик технических и в том числе информационных компьютерных систем [1—6].

При построении марковских моделей система рассматривается в различных работоспособных и отказавших состояниях, каждое из работоспособных состояний характеризуется различной эффективностью функционирования и запасом ресурсов обеспечения надежности. Переход между состояниями системы происходит в момент отказа или восстановления элемента системы. Рассматриваемый процесс переходов описывается моделью дискретных состояний с непрерывным временем.

Используемая для анализа надежности системы модель дискретных состояний позволяет отобразить функционирование системы с накоплением отказов (деградации), а для систем с восстановлением — отразить влияние различных дисциплин обслуживания.

Случайный процесс называется марковским, если для любого момента t₀ вероятность состояния системы в будущем (t > t₀) зависит только от состояния в настоящем (t = t₀) и не зависит от того, когда п каким образом система пришла в это состояние (не зависит от предыстории).

Предположения, принятые для марковского процесса, формулируются по ГОСТ Р 51 901.15—2005 следующим образом:

• • переходы состояний являются статистически независимыми событиями;
• • интенсивность отказов X и интенсивность восстановлений р постоянны во времени для каждого состояния (при переходе в другие состояния эти интенсивности могут меняться);
• • вероятности перехода из одного состояния в другое в интервале времени At (At — мало) при отказах и восстановлениях задаются величинами XAt и pAt соответственно [ 1 ].

Для случайного процесса с непрерывным временем, представляемого марковским процессом, требуется, чтобы интервалы времени между соседними переходами были распределены по экспоненциальному закону.

Таким образом, для марковского процесса вероятности перехода из некоторого г-го в j-e состояние за время At:

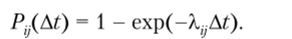
Предположим, что интервал времени At достаточно мал. Тогда, разлагая ехр (^At) в ряд по степеням k_:jAt при At —* 0 и пренебрегая величинами высшего порядка малости, получим вероятность перехода из одного состояния в другое за бесконечно малый интервал времени:

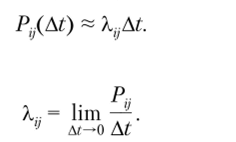
При этом Рассмотрим элемент, который может находиться в одном из двух состояний — работоспособном или отказавшем.

Выделим некоторый произвольный момент времени t и момент t + At и отстоящий от него на малый интервал времени At. Вероятность отказа элемента на малом интервале At оценим как /.At, а вероятность восстановления на этом интервале — как рД/.

Пусть в момент времени t рассматриваемый элемент находится в работоспособном состоянии А с вероятностью Р (А), а в неработоспособном состоянии В — с вероятностью Р (В). Вероятность нахождения элемента в работоспособном состоянии Л, к моменту времени (t + At) находим по формуле полной вероятности:

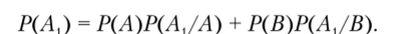
Учитывая, что вероятность перехода из неработоспособного состояния В в работоспособное состояние А, за время At определяется как Р (А_{/В) = = рД?, а вероятность того, что за время At отказа не произойдет, — как Р (Л/Л,) = 1 — ХАt, и что (по определению коэффициента готовности).

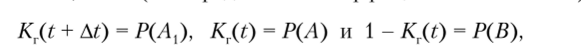
формула полной вероятности представляется как откуда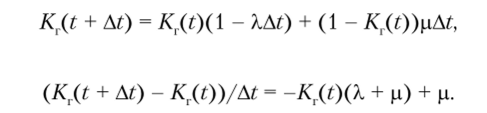

Определяя предел при At —* 0, получаем.

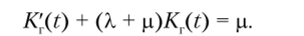
Решая полученное линейное дифференциальное уравнение, находим.

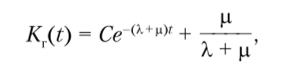
где постоянная С находится с учетом вероятности работоспособного состояния элемента в начальный момент времени t = 0.

При работоспособности элемента в момент времени t = 0: К_г(0) = 1 и е^_<�х+и)0 = 1 находим.

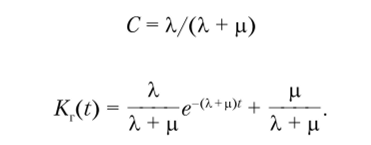
и Если в начальный момент времени t = 0 объект неработоспособен, то КХ0) = 0, е <^х+«>° = 1, С = -х/(Х + р).

Соответственно, находим.

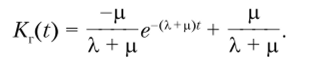
График зависимости коэффициента готовности от времени (в нестационарном режиме) КХО показан на рис. 9.1. Кривая 1 соответствует зависимости нестационарного коэффициента готовности элемента от времени при работоспособности исходного состояния, а кривая 2 — при неработоспособ;

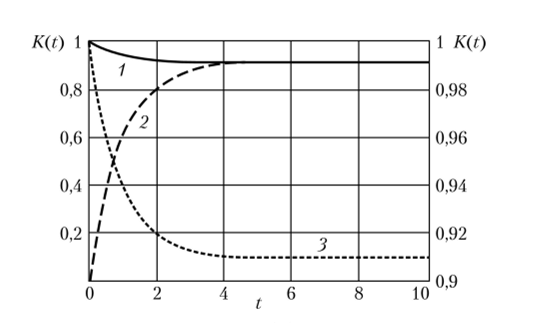
Рис. 9.1. Сходимость нестационарного коэффициента готовности к стационарному.

пости исходного состояния. Расчет проведен при р = 1 1/чД = 0,1 1 /ч. Кривая 3 уточняет расчет нестационарного коэффициента готовности при работоспособности исходного состояния по дополнительной оси K (t) в диапазоне значений от 0,9 до 1.

Графики подтверждают, что независимо от начального состояния нестационарный коэффициент готовности K_t.(0 стремится к постоянному значению стационарного коэффициента готовности k_r = р/(Х + р).