Системы линейных уравнений. 
Метод Гаусса

А. В качестве примера рассмотрим систему трех уравнений с двумя неизвестными х, у

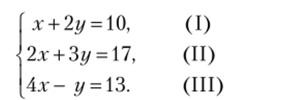
Решением системы уравнений называется упорядоченная пара чисел (г; у), которая обращает каждое уравнение системы в числовое равенство (тождество). Проверка показывает, что упорядоченная пара (4; 3), т. е. х = 4, у = 3, является решением данной системы.

Система уравнений, имеющая хотя бы одно решение, называется совместной.

Решить систему — это значит найти все ее решения или показать, что система не имеет решений (в этом случае ее называют несовместной).

Для решения систем линейных уравнений существуют разные приемы. Рассмотрим метод Гаусса, преобразующий данную систему в более простую. На первом шаге, сохранив неизменным первое (опорное) уравнение, используем его для преобразования второго и третьего уравнений таким образом, чтобы в них исчезло неизвестное х. С этой целью из второго уравнения вычитаем почленно первое уравнение, умноженное на 2, а из третьего — первое уравнение, умноженное на 4. Получаем:

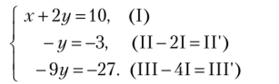
(справа схематично указаны выполненные преобразования).

На втором шаге, используя в качестве опорного новое второе уравнение, преобразуем новое третье уравнение так, чтобы в нем исчезло у. Получаем:

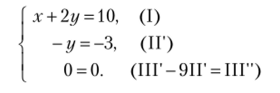
Удалив последнее уравнение как тривиальное (0 = 0), получаем треугольную систему:

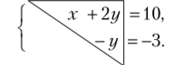
Из второго уравнения находим: у = 3. Подставив это значение в первое уравнение, получаем:

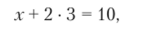
откуда х = 10−6 = 4.

Полученная упорядоченная пара (4; 3) уже была испытана в качестве решения. Теперь мы убедились в том, что это решение единственное.

Приведем еще несколько примеров.

Пример 2.1.

Рассмотрим систему:

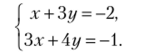
Применяя метод Гаусса, преобразуем второе уравнение, вычитая из него первое уравнение, умноженное на 3:

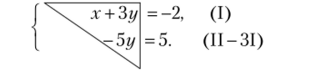
Получили систему треугольного вида. Из последнего уравнения заключаем, что у = -1. Подставляя это значение в первое уравнение, находим хг.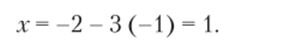

Таким образом, найдено единственное решение системы:

J* = l, b=-i.

Пример 2.2.

Применяя метод Гаусса к системе:

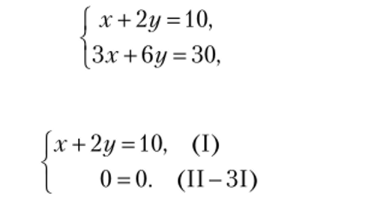
получаем:

После удаления второго (тривиального) уравнения остается одно уравнение с двумя неизвестными. В этом примере исходная система имеет бесконечное множество решений. Чтобы найти общее решение системы, надо одно из неизвестных, главное, выразить через другое — свободное.

Пусть х — главное неизвестное, а у — свободное неизвестное. В этом случае общее решение системы записывается следующим образом:

Чтобы найти какое-нибудь частное решение следует свободному неизвестному придать определенное числовое значение. Например, полагая у = 1, находим х = 8. Таким образом, (8; 1) — частное решение системы.

Пример 2.3.

Применив метод Гаусса к системе: получаем: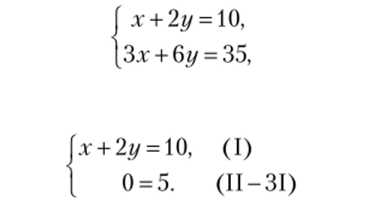

Полученное числовое «равенство» не удовлетворяется ни при каких значениях х и у. Поэтому решений у исходной системы нет и она является несовместной.

Рассмотренные три примера исчерпывают все принципиально различные случаи решения систем двух линейных уравнений с двумя неизвестными.

Применяя метод Гаусса к системе общего вида:

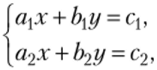
можно убедиться, что имеет место один из трех возможных исходов.

1. Если — ⁼ ~г~ ⁼ — у то система имеет бесконечное мно;

а₂ Ъ₂ с₂

жество решений.

а_л by с_у

2. Если — = — ф —, то система несовместна.

а₂ Ь₂ с₂

3. Если то система имеет единственное реше;

а₂ Ь₂

ние.

Б. Метод Гаусса позволяет решать системы и с большим числом уравнений и неизвестных. Приведем примеры систем трех линейных уравнений с тремя неизвестными. Решением системы уравнений с гремя неизвестными называется упорядоченная тройка чисел (х; у z), которая обращает каждое из уравнений системы в числовое равенство (тождество).

Пример 2.4.

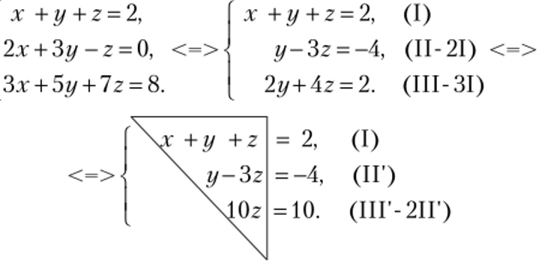
Полученная система имеет треугольный вид. Из последнего уравнения находим 2=1, затем из предпоследнего определяем.

у = - 4 + 3 = - 1 и, наконец, из первого находим: * = 2−1 + 1= 2. Получили единственное решение: (2; -1; 1).

Пример 2.5.

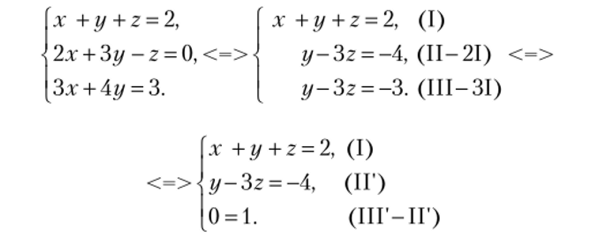
Поскольку третье соотношение в последней системе фактически является неравенством, то решений нет и исходная система уравнений несовместна.

Пример 2.6.

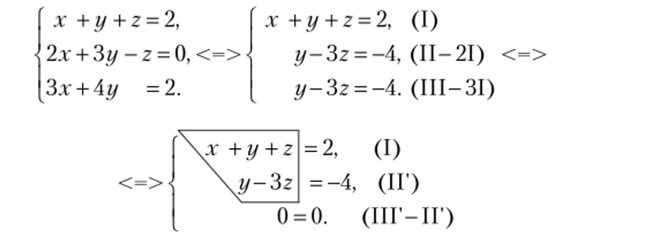
После преобразований получаем трапецеидальный вид системы линейных уравнений. В этом случае система имеет бесконечное множество решений. Пусть z — свободное неизвестное, а х, у — главные неизвестные. Последовательно выражая главные неизвестные через свободные, найдем общее решение. Из второго уравнения получаем: у = 3z — 4; подставляя это выражение в первое уравнение, находим: x=2-y-z = 2−3z + 4- z = 6−4z. Таким образом, общее решение имеет вид:

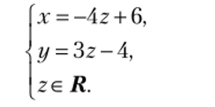
Найдем одно их частных решений. Например, полагая 2=1, из общего решения находим: х = 2, у = -1. Таким образом, частное решение: (2; - 1; 1).

Рассмотренные три примера исчерпывают все принципиально возможные случаи решения систем трех линейных уравнений стремя неизвестными.

В. Вернемся к системе двух уравнений общего вида с двумя неизвестными:

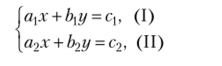
и предположим, что коэффициенты при неизвестных не пропорциональны:

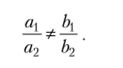
В этом случае метод Гаусса гарантирует, что система уравнений имеет единственное решение. Получим формулы, определяющие это решение через коэффициенты и свободные члены данных уравнений.

Полагая, что а_л Ф 0, преобразуем второе уравнение:

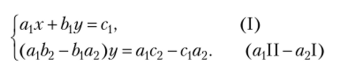
Поскольку в силу предположения о непропорциональности коэффициентов имеем: аф₂ — Ь_{а₂ * 0, то из второго уравнения у определяется однозначно:

Исходную систему уравнений можно преобразовать подругому — так, что из преобразованного второго уравнения, не содержащего у, однозначно определяется х:

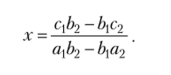
Для запоминания полученных формул используем важное в алгебре и ее приложениях понятие определителя.