Изолированные особые точки и теория вычетов

Классификация изолированных особых точек

Пусть zq — особая точка функции /(г), т.с. f (z) но является аналитической в этой точке (в частности, может быть не определена в ней). Если найдется такая проколотая окрестность точки zq (т.е. множество О < z — zq < Я), в которой f (z) аиалитична, то zo называется изолированной особой точкой функции f (z). Данное определение сохраняется и в случае zn = оо, если иод проколотой окрестностью точки zq = оо понимать множество z > Я — внешность некоторого круга с центром в начале координат. Другими словами, особая точка zq называется изолированной, если найдется такая окрестность этой точки, в которой ист других особых точек, отличных от zq. Всюду в дальнейшем мы рассматриваем только особые точки однозначного характера (функция f (z) предполагается однозначной).

В зависимости от поведения функции f (z) при z —> zq различают три типа особых точек. Изолированная особая точка zq функции f (z) называется:

1) устранимой особой точкой, если существует конечный предел.

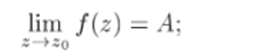
2) полюсом, если существует предел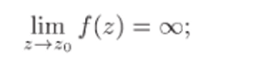

3) существенно особой точкой, если f (z) не имеет ни конечною, ни бесконечного предела при z -> zq.

П р и м е р 26.1. Покажем, что все три типа особых точек реализуются. Рассмотрим f (z) = Точка zq = 0 является изолированной особой точкой этой функции. Используя формулу (22.12), получим разложение.

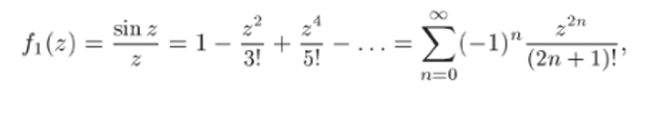
из которого следует, что существует lim fi (z) = 1. Поэтому zq = 0 яв;

г->0.

ляется устранимой особой точкой функции fi (z).

Функция f‘j (z) = -—- имеет полюс в точке zo = 1, поскольку.

2r «X.

lim-7 = оо.

г-«1 2 — 1.

Рассмотрим теперь функцию }з (z) = е¹^^г и покажем, что zo = О является существенно особой точкой этой функции. При стремлении z к нулю по действительной оси левый и правый пределы функции /з(z) различны: lim с¹/¹ = 0, lim с¹/* = ос. Отсюда следует, х—>0—0 х—>0+О что f:i (z) не имеет ни конечного, ни бесконечного предела при 2 —> О, т. е. zq ⁼ О — существенно особая точка этой функции. (Заметим, что при стремлении точки z — iy к нулю по мнимой оси функция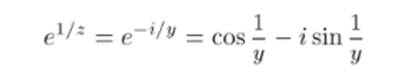

вообще не имеет предела.).

Существуют, конечно, и неизолированные особые точки. Например. функция имеет полюсы в точках z_n = —, п = ±1, ±2,…

Следовательно, Zq = 0 является неизолированной особой точкой этой функции: в любой (сколь угодно малой) окрестности этой точки имеются другие особые точки г_п.

Пусть zo — конечная изолированная особая точка функции f{z). Тогда f (z) аналогична в некоторой проколотой окрестности 0 < < |г — Zo < R точки zo эту окрестность можно рассматривать как кольцо с внутренним радиусом г = 0. По теореме 25.1 в рассматриваемой окрестности функцию f (z) можно разложить в ряд Лорана (25.2). Мы покажем, что поведение функции при 2 —> zq (т.е. тип особой точки zo) зависит от вида главной части разложения (25.2); этим обстоятельством и объясняется происхождение термина «главная часть».

Т е о р е м a 2G.2. Изолированная особая точка zo функции f (z) является устранимой тогда и только тогда, когда лораповскос разложение в проколотой окрестности этой точки имеет оид

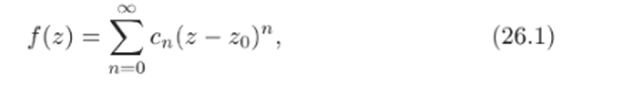
т.е. состоит только из правильной части, а все коэффициенты главной части равны пулю.

Доказательство. 1. Пусть zo — устранимая особая точка. Докажем, что лорановское разложение функции f (z) имеет вид (26.1). Так как особая точка zo устранимая, то существует конечный предел lim f (z) = А. Следовательно, f (z) ограничена в некоторой проколотой окрестности 0 < z — zq < R точки zo, т. е. }(z) < М для всех z из этой окрестности. Возьмем любое р. U < р < /?|, и воспользуемся формулами (25.3) для коэффициентов ряда Лорана:

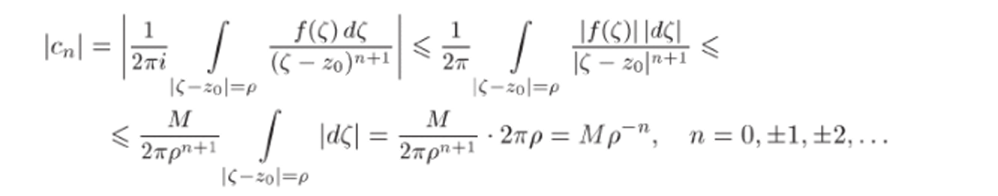
Для коэффициентов главной части разложения п = — 1,—2,… Для таких значений п имеем р~^п -э 0 при р —> 0. Так как значение р может быть выбрано сколь угодно малым, то и Мр~" может быть сколь угодно малым. Поскольку |с_т,| ^ Мр~^п и с" не зависят от р, то с" = 0 при и = — 1, —2,…, что и требовалось доказать.

2. Предположим теперь, что лорановское разложение имеет вид (26.1). Ряд (26.1) является степенным рядом и. следовательно, сходится не только в проколотой, но и во всей окрестности z — zq < < R. включая и точку zo; его сумма S (z) аналитична при z < R и S (z) = }(z) при 0 < z — zo < R. Поэтому существует конечный предел lim }(z) = Пт 5(г) = 5(го) — Следовательно, особая точка zq.

Z—>Zo Z—*Zo

устранимая. Теорема доказана.

Замечание. Из доказательства теоремы следует, что в проколотой окрестности 0 < z — zo < R устранимой особой точки функция f (z) совпадает с функцией 5(г), аналитической во всей окрестности z — zo < R. Поэтому, если мы положим /(го) = S (zq), то, не меняя значений функции f (z) ни в каких точках проколотой окрестности, мы сделаем эту функцию аналитической в го, т. е. «устраним» особенность. Этим и объясняется термин «устранимая особенность». Такие точки естественно считать правильными, а не особыми точками функции f (z).

Рассмотрим, например, функцию.

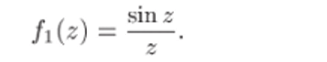
В примере 26.1 было показано, что Пт Ыг) = 1. т. е. особая точка.

z—>0.

zq = 0 устранимая. Полагая /i (0) = 1, мы тем самым устраним особенность и получим функцию, аналитическую в точке zq = 0 (и во всей плоскости С).

Дадим теперь характеристику полюсов в терминах лорановских разложений.

Теорема 26.3. Изолированная особая точка Zo функции f (z) является полюсом тогда и только тогда, когда главная часть разложения Лорана с центром Zq имеет лишь конечное чиаао отличных

от нуля коэффициентов с_п:

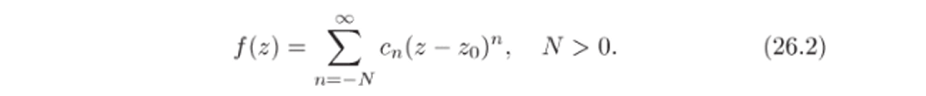
Доказательство. 1. Пусть zq — полюс, т. е. lim /(z) = оо.

z—*z о Докажем, что лорановское разложение функции f (z) имеет вид (2G.2). Так как lim f (z) = оо. то существует проколотая окрестность точ;

Z—tZo

ки zq. в которой f (z) аналитична и не имеет нулей. Тогда функция g (z) = 1 /f (z) тоже будет аналитической в этой проколотой окрестности, причем lim g (z) = 0. Следовательно, Zo является устранимой *—? *0.

особой точкой функции g (z). Доопределим g (z) в точке zo, положив g (zo) = 0. Тогда g (z) станет аналитической во всей окрестности (не проколотой) точки z₀, причем z₀ будет ее изолированным нулем. Обозначим через N кратность (порядок) этого нуля. Как было показано в § 23, в окрестности точки zq функция g (z) представима в виде (см. (23.2))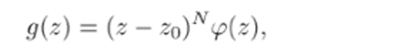

причем (z$) ф 0 и y>(z) аналитична в некоторой окрестности точки zo- Так как ip (z) непрерывна в точке zo и g>(zo) Ф 0″ то ip (z) не имеет нулей и в некоторой окрестности этой точки. Поэтому функция 1 /-p (z) будет также аналитической в этой окрестности и, следовательно, разлагается в ней в ряд Тейлора:

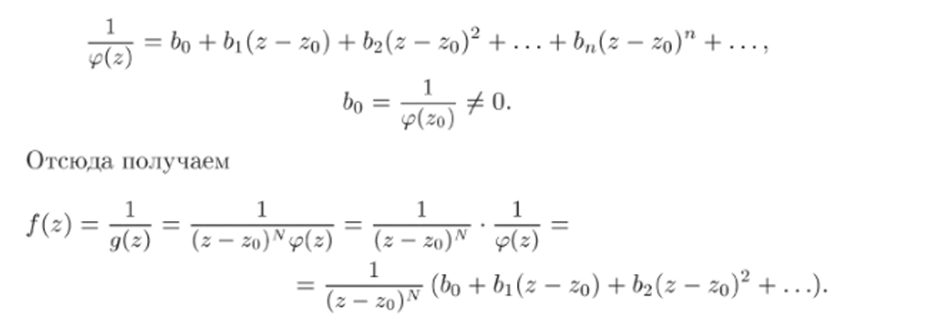
Раскрывая скобки и меняя обозначения коэффициентов, запишем последнее разложение в виде.

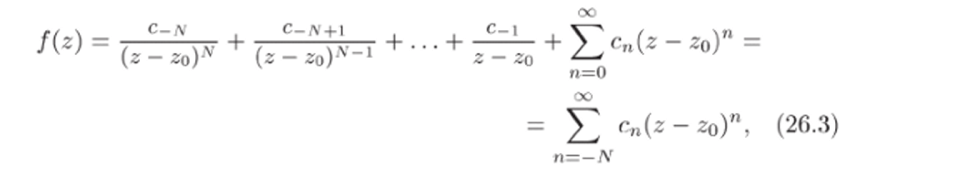
где c_jv = 1>о ф 0. Таким образом, главная часть лорановского разложения функции /(г) содержит лишь конечное число членов; мы пришли к искомому равенству (26.2).

2. Пусть в проколотой окрестности точки го функция }(z) представляется лорановским разложением (26.2) (в более развернутом виде см. (26.3)), главная часть которого содержит лишь конечное число членов, причем с- д' ф 0. Надо доказать, что Zq — полюс функции f (z). Умножая равенство (26.3) на (г — гo)^iV, получим функцию.

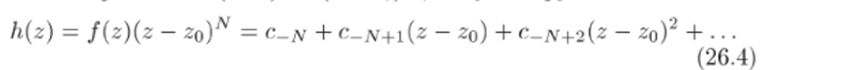
Ряд в (26.4) является степенным рядом, сходящимся к аналитической функции не только в проколотой, но и во всей окрестности точки Zq. Поэтому функция h (z) станет аналитической в этой окрестности, если доопределить ее в го, положив h (zo) = с_дг ф 0. Тогда.

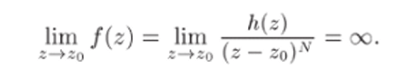
Таким образом, точка го является полюсом, и теорема 26.3 доказана.

Кратность (порядок) нуля го функции g (z) = 1//(г) называется порядком полюса го функции /(г). Если N — порядок полюса го, то g (z) = (г — Zo)^Nip (z), причем (го) Ф 0, и, как показано в первой части доказательства теоремы 26.3, разложение функции /(г) имеет вид (26.3), где c_/v ф 0. Обратно, если /(г) раскладывается в ряд (26.3) и e-я Ф 0, то.

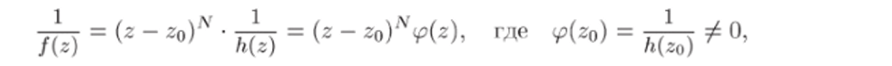
т.с. N — порядок полюса функции /(г). Таким образом, порядок полюса zq функции /(г) равен номеру старшего ненулевого коэффициента главной части лорановского разложения в проколотой окрестности точки zq (т.е. равен такому числу N, что с_дг ф 0 и Сп = 0 при п > N).

Докажем следующее утверждение, удобное) для применений.

Следствие 26.4. Точка zq является полюсом порядка N фикции /(г) тогда и только тогда, когда /(г) представима в виде

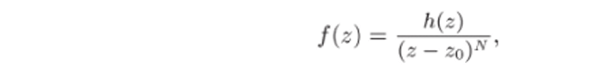
где h (z) — аналитическая функция в окрестности точки го и h (zo) ф 0.

Доказательство. Функция cp (z) = l/h (z) аналитична в некоторой окрестности точки гоУсловие следствия 26.4 равносильно следующему:

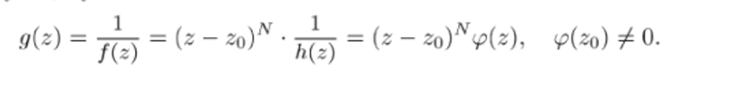
Поэтому zq - нуль кратности N функции g (z). а значит, и полюс кратности N функции /(2).

II р и м е р 26.5. Найти изолированные особые точки функции 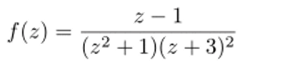и определить их тип.

Р е ш е н и е. Особыми будут точки, в которых (z² + 1 )(z + З)² = 0. Если z² Л- 1 = 0, то 2 = ±г если (z 4- З)² = 0, то z = -3. Поэтому функция имеет три особые точки z = г, 22 = —г, Z3 = — 3. Рассмотрим z:

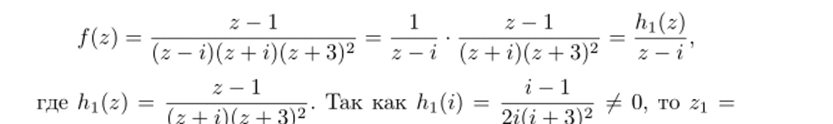
г — полюс первого порядка (мы воспользовались следствием 26.4). Аналогично доказывается, что 22 = —i тоже полюс первого порядка. Для 2з имеем:

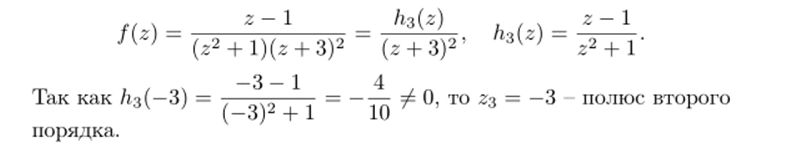
Перейдем к рассмотрению существенно особых точек.

Теорема 26.6. Изолированная особая точка zq функции f (z) является существенно особой тогда и только тогда, когда главная часть разложения Лорана с центром zq имеет бесконечно много отличных от. нуля, коэффициентов с_п.

Доказательство. Теорема 26.6 непосредственно вытекает из теорем 26.2 и 26.3. Действительно, если точка zq — существенно особая, то главная часть лорановского разложения не может отсутствовать либо содержать конечное чиСмТО членов (в противном случае точка Zq будег либо устранимой, либо полюсом). Поэтому число членов в главной части должно быть бесконечным.

Обратно, если главная часть содержит бесконечно много членов, то Zq не может быть ни устранимой точкой, ни полюсом. СледоватСмЧьно, эта точка — существенно особая.

Согласно определению, существенно особая точка характеризуется тем, что функция /(2) не имеет ни конечного, пи бесконечного предела при z —> zq. Более полное представление о том, насколько нерегулярным является поведение функции в окрестности существенно особой точки, дает следующая теорема.

Теорема 26.7 (теорема Сохоцкого). Если zq — существенно особам, точка функции f (z), то для любого комплексного числа Л, включая, А = оо, найдется последовательность точек z_n такая, что z_n -> zo и lim f (z_n) = А.

п->ос

Доказательство. Рассмотрим вначале случай А = оо. В первой части доказательства теоремы 2G.2 мы установили, что если f (z) ограничена в некоторой проколотой окрестности точки го, то все коэффициенты с", п = — 1, — 2,… главной части равны нулю (и, следовательно, особенность в го устранимая). Так как по условию го существенно особая точка, то в любой проколотой окрестности точки го функция /(г) является неограниченной. Возьмем некоторую щхжолотую окрестность 0 < |г — го| < Я, в которой /(г) является аналитической. В этой окрестности найдется точка Z, такая что f (zi) > 1 (если бы |/(г)| < 1 во всех точках, то /(г) была бы ограниченной). Точно также в проколотой окрестности 0 < z — zo < Я/2 найдется точка z-2, в которой |/(гг)| > 2, и т. д.: в проколотой окрестности О < |г — го| < Я/n найдегся точка г", в которой |/(г_п)| > 71. Очевидно, что г" -э го и lim /(г") = оо. Таким образом, в случае Л = оо теорема 26.7.

п —"ос доказана.

Пусть теперь А ф оо. Предположим вначале, что найдегся проколотая окрестность 0 < |г — го| < #i, в которой /(г) / Л. Тогда функция Ф (з) =.

= -гг—--- будет аналитической в этой проколотой окрестности и, сле;

/(г) — А

довательно, го является изолированной особой точкой функции Ф (г). Покажем. что го — существенно особая точка Ф (г). Пусть это неверно. Тогда существует предел lim Ф (г), конечный либо бесконечный. Поекольку.

/(г) = Л +, то тогда существует и Нш /(г), что противоречит усло;

Ф (г) ~ :-*z₀

вию теоремы. Таким образом, го — существенно особая точка функции Ф (г). Согласно доказанному выше, найдется последовательность точек г_п, такая что г_п го и lim Ф (г_п) = оо. Отсюда п—>оо.

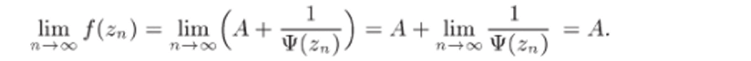
Мы доказали нужное утверждение в предположении, что /(г) Ф А в некоторой проколотой окрестности точки гоПредположим теперь, что это неверно, т.с. в любой сколь угодно малой проколотой окрестности точки го найдется такая точка г', что /(г') = Л. Тогда для любого п в проколотой окрестности 0 < |г — го| < Я/n можно выбрать такую точку г". Мы получим последовательность точек, для которых /(г_п) = Л и г_п —" го. Поэтому и lim f (z_u) = Л. Таким образом, нужное утверждение справедливо п—юо во всех случаях, и теорема 26.7 доказана.

Согласно теореме 26.7 (Сохоцкого), в любой (сколь угодно малой) проколотой окрестности существенно особой точки функция /(г) принимает значения, сколь угодно близкие к любому числу из расширенной комплексной плоскости С.

Для исследования изолированных особых точек часто бывают полезными уже известные тейлоровские разложения основных элементарных функций.

П р и м е р 2G.8. Определить тин особой точки zq = 0 для функции.

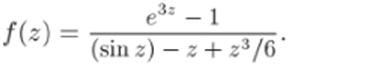
Решен и е. Разложим числитель и знаменатель в ряд Тейлора по степеням г. Подставляя в (22.11) 3z вместо г и вычитая 1, получим.

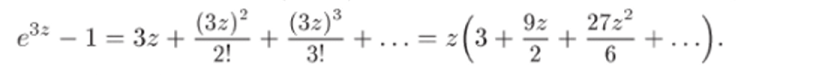
Используя (22.12), получим разложение знаменателя:

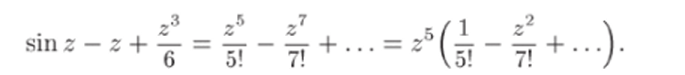
Ряды в этих разложениях сходятся во всей комплексной плоскости €. Имеем.

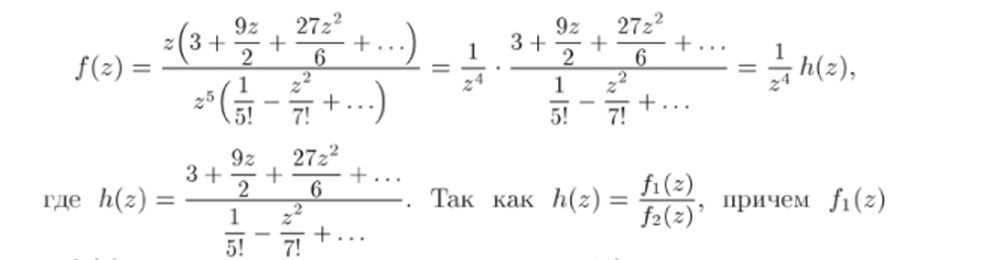
и /2(2) анаиитичны в окрестности точки zo = 0 (и даже во всей плоскости) и /2(20) Ф 0, то h (z) также аналитична в некоторой окрестности точки г<) = U: при этом /*(0) = 3 • 5! Ф 0. Согласно следствию 26.4, точка Zo = 0 является полюсом порядка N = 4.

II р и м е р 26.9. Найти особые точки функции f (z) = sin j^- и определить их тип.

Р е in е и и е. Функция имеет единственную конечную особую точку zq = 1. В остальных точках из С функция w = -—- аналитична; следовательно, и функция sin w будет аналитической.

Подставляя в разложение синуса (22.12) — вместо г, получим.

V 1.

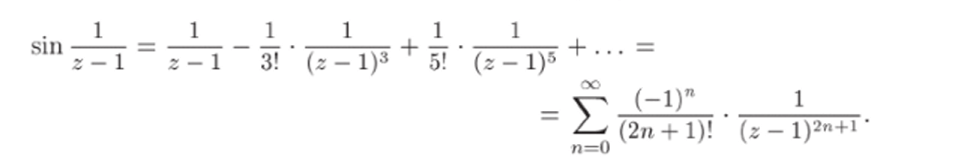
Мы получили разложение функции sin —в ряд Лорана в проколотой окрестности точки 2о = 1. Поскольку полученное разложение содержит бесконечно много членов с отрицательными степенями (г — 1), то zq = 1 — существенно особая точка (в данном случае лорановское разложение состоит только из главной части, а правильная часть отсутствует).

Заметим, что установить характер особенности в данном случае можно было и непосредственно из определения, не прибегая к разложению в ряд. Действительно, существуют последовательности {г',} и {2″ }, сходящиеся к zo = 1, и такие, что f (z'_n) = 1, /(2″) = 0 (укажите такие последовательности самостоятельно). Значит, f (z) не имеет предела при z —> 1 и, следовательно, точка zq — 1 является существенно особой.

Введем понятие лорановского разложения функции в окрестности точки Zq = 00 и рассмотрим связь разложения с характером особенности в этой точке. Отметим, что определения изолированной особой точки и ее типа (устранимая, полюс либо существенно особая) переносятся на случай zq = ос без изменений. Но теоремы 26.2. 26.3 и 26.6, связанные с характером лорановских разложений, нуждаются в изменении. Дело в том, что члены c_n(z — 2о)^п. п = —1,—2,…, главной части, определяющие «‘нерегулярность» функции вблизи конечной точки Zq, при стремлении 2 к оо будут вести себя «правильно» (стремиться к 0). Напротив, члены правильной части с п = 1,2,… будут стремиться к оо; они и определяют характер особенности в Zq = оо. Поэтому главную часть разложения в окрестности оо будут составлять члены с положительными степенями п, а правильную — с отрицательными.

Введем новое переменное w = 1 /2. Функция tv = 1 /2, доопределенная так, что щ (оо) = 0, взаимно однозначно н конформно отображает окрестность z > R точки zq = 00 в окрестность |ш| <1//? 'гонки wq = 0. Если функция f (z) аналитичиа в проколотой окрестности R < z < 00 точки Zq = ос, то функция G (w) = f (l/w) будет аналитической в щхжолотой окрестности 0 < |ш| < 1/7? точки wo = 0. Так как при 2 —> оо будет w —> 0, то.

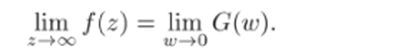
Поэтому G (w) имеет в точке wq = 0 особенность того же типа, что f (z) в точке Zq = 00. Разложим функцию G (w) в ряд Лорана в проколотой окрестности точки wo = 0:

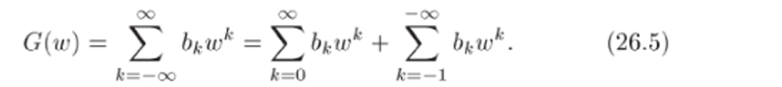
Суммы в правой части (26.5) представляют правильную и главную части разложения соответственно. Перейдем к переменному z, подставив w = 1/z: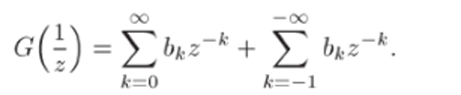

Обозначая п = —А*, 6* = 6_" = с_п и замечая, что G (l/z) = f (z), получим.

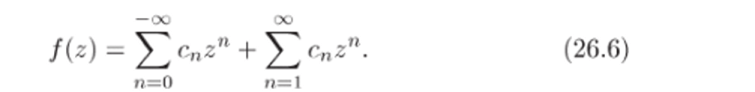
Разложение (2G.G) называется разложением Лорана функции f (z) в проколотой окрестности точки zq = оо. Первая сумма в (2G.6) называемся правильной частью, а вторая сумма — главной частью этого разложения. Поскольку эти суммы соответствуют правильной и главной частям разложения (26.5), то для разложения (26.6) справедливы аналоги теорем 26.2, 26.3 и 26.6. Так, аналогом теоремы 26.2 будет следующая теорема.

Теорема 26.10. Изолированная особая точка Zq — ос (функции /(г) является устранимой тогда и только тогда, когда лорановское разложение в проколотой окрестности этой точки имеет вид

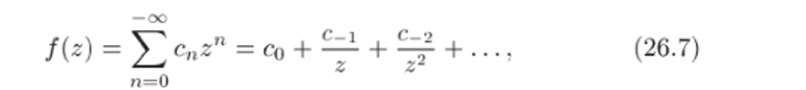
т.с. состоит только из правильной части.

Положим /(оо) = со. Функция, определенная рядом (26.7), сходящимся в окрестности z > R точки 2о = ос, называется аналитической в точке zо = оо. (Заметим, что это определение равносильно аналитичности функции G (w) в точке wo = 0.).

При м е р 26.11. Исследовать особую точку zq = оо функции.

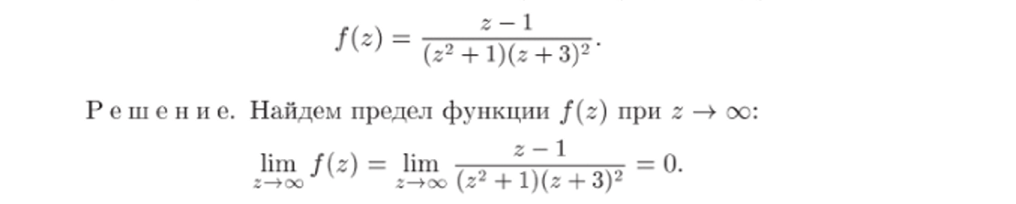
Так как предел конечен, то zo = оо — устранимая особая точка функции /(г). Если положить /(оо) = lim J (z) = 0, то f (z) станет анали;

г—юо.

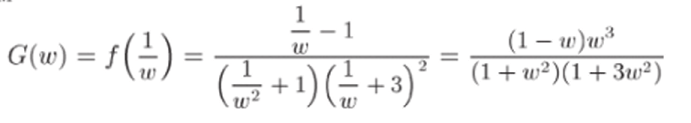
тической в точке Zo = ос. Укажем, как найти соответствующее разложение (26.7). Перейдем к переменному w = 1 fz. Подставляя z = 1 /?е, получим.

(последнее равенство справедливо в проколотой окрестности точки шо = 0, но мы доопределим (7(0) = 0). Полученная функция имеет особые точки w = ±i, w = —1/3, а в точке Wq = 0 является аналитической. Раскладывая функцию G (w) по степеням w (как это делалось в примере 25.7) и подставляя в полученный степенной ряд w = 1/z, можно получить разложение (26.7) функции f (z).

Теорема 26.3 для случая zo = оо перепишется в следующем виде.

Теорема 26.12. Изолированная особая точка го = ос функции f (z) является полюсом тогда и только тогда, когда главная часть разложения Лорана (26.6) имеет лишь конечное число отличных от нуля коэффициентов с":

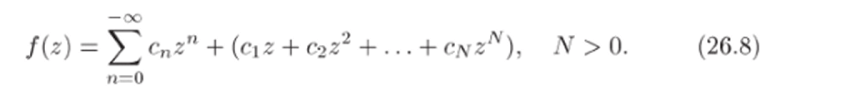
Здесь ряд является правильной частью, а многочлен в скобках — главной частью разложения. Кратность полюса в ос определяется как кратность полюса wq = 0 функции G (z). Легко видеть, что кратность полюса совпадает с числом N в (26.8).

Q п | (я² + 1)(з+3)²

Задача. Покажите, что функция f (z) =-—-— имеет в.

2 ^— 1.

точке zo = оо полюс порядка 3.

Теорема 26.6 о существенно особой точке переписывается для случая zo = ос почти дословно, и мы не останавливаемся на этом подробно.