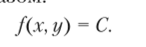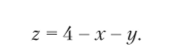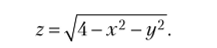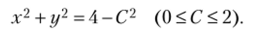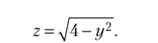Геометрические аспекты функции двух переменных

Область определения и линии уровня

Каждую из допустимых пар значений х, у будем воспринимать как пару координат точки Р (х, у) на координатной плоскости хОу. Множество точек Р (х, у) образует область определения функции z = f (x, у) на плоскости хОу. Если область определения не задана, именно с ее нахождения начинают исследование функции.

Чтобы начертить график функции двух переменных, часто требуется немалое пространственное представление. Поэтому исследование обычно начинают с рассмотрения тех свойств функции, которые можно обнаружить, не покидая плоскость хОу и рассматривая более детально ее область определения. Например, полезно найти в области определения так называемые линии уровня, в точках которых функция принимает одно и то же значение.

Пусть функция z = f (x, у) принимает в точках линии уровня значение С. Тогда уравнение линии уровня записывается следующим образом-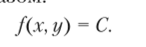

Левая часть этого уравнения может налагать на параметр С определенные ограничения. Множество допустимых значений С порождает однопараметрическое семейство линий уровня, которое заполняет целиком область определения функции.

В следующих примерах укажем на координатной плоскости хОу области определения некоторых функций и в каждом случае построим несколько линий уровня, отметив при этом те постоянные значения С, которые принимает данная функция на соответствующей линии уровня.

Пример 9.1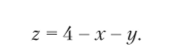

Эта формула не содержит никаких ограничений на значения аргументов, поэтому область определения данной, как и вообще любой линейной функции, — вся координатная плоскость. Если исходному уравнению линий уровня: 4 — х — у = С придать вид: х + у = 4 — С, то становится очевидно, что линии уровня суть параллельные прямые, заполняющие всю плоскость хОу (рис. 9.1).

Пример 9.2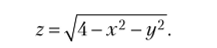

Так как подкоренное выражение не должно быть отрицательным, эта формула содержит ограничения на аргументы. Неравенство 4-х²— у² >0 выполняется для координат точек внутри и на границе круга х'¹ + у² =4 радиуса 2 с центром в начале координат — это и есть область определения данной функции.

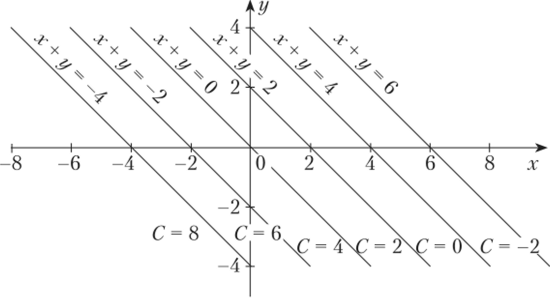
Рис. 9.1.

Уравнение линии уровня yjA-x² — у² = С запишем в виде:

Следовательно, линии уровня — концентрические окружности с центром в начале координат. При С = 2 окружность вырождается в точку (рис. 9.2).

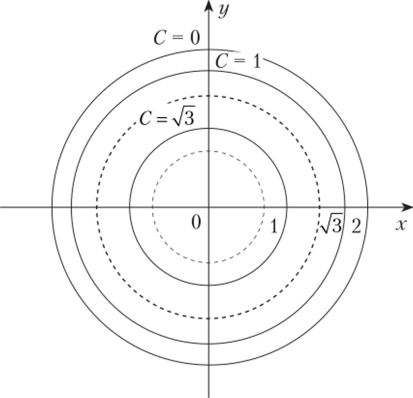
Рис. 9.2.

Пример 9.3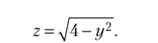

В этом примере требование неотрицательности подкоренного выражения налагает ограничение только на у. Область определения задается неравенствами: -°°<�х<�°°;-2<�у<2 и представляет собой полосу, включающую граничные прямые у = -2иу = 2. Уравнению линии уровня: ^4-у² = С придадим вид: у² =4-С² (0 <�С < 2). Следовательно, каждая линия уровня распадается на пару параллельных прямых:

у = ±yj4-C² . При С = 2 обе прямые совпадают с осью Ох. В совокупности семейство линий уровня данной функции заполняет полосу: -2<�у<2 (рис. 9.3).

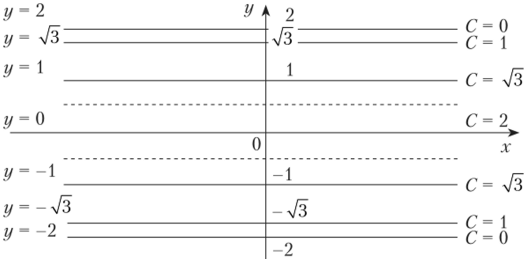
Рис. 9.3.