Аппроксимация, устойчивость, сходимость разностных схем. 
Основные понятия

Рассмотрим некоторую задачу, определяемую дифференциальным уравнением и граничными условиями. Запишем ее в операторной форме.

где через L обозначен некоторый дифференциальный оператор, действующий на искомую функцию и, через f — правая часть. Примем, что оператор L включает как дифференциальные уравнения, так и граничные условия. На некоторой разностной сетке строим разностный оператор L_h, действующий на сеточную функцию u_h. Примером дифференциального оператора является оператор Лапласа Д, а соответствующий ему разностный оператор возникает при аппроксимации вторых производных разностными отношениями (4.9) и (4.10).

Величина 6/_А называется НЕВЯЗКОЙ, и при подстановке точного решения уравнения (4.21) в оператор L_h имеем.

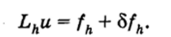
РАЗНОСТНАЯ СХЕМА называется АППРОКСИМИРУЮЩЕЙ на решении, если норма невязки стремится к нулю при стремлении к нулю шага разностной схемы, т. е. ||б/_А|| -" 0 при h -" 0.

Если при этом постоянная С_р не зависит от шага h и норма невязки удовлетворяет условию ||5/J| < С_рЛ^р, то говорят, что разностная схема имеетр-й порядок аппроксимации или разностная схема аппроксимирует дифференциальный оператор с порядком р. Например, разностный оператор

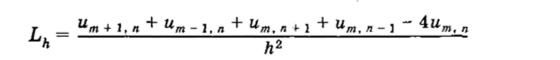
Э² Э²

аппроксимирует оператор Лапласа Д — т—т + —- со вторым по;

дх⁴ он⁴

рядком точности, *.

РАЗНОСТНАЯ СХЕМА называется СХОДЯЩЕЙСЯ, если норма разности точного и приближенного решений ||u — н_А|| стремится к нулю при стремлении к нулю шага разностной сетки.

Если при этом ||и — н_А[| < C_qh то говорят, что разностная схема имеет q-n порядок точности или имеет место сходимость с порядком q.

Порядок аппроксимации дифференциального уравнения не всегда совпадает с порядком точности разностной схемы, так как порядок точности разностной схемы зависит как от аппроксимации дифференциального уравнения, так и от аппроксимации граничных условий.

Не всякая аппроксимирующая схема является сходящейся. В связи с этим важным является понятие устойчивости разностной схемы.

УСТОЙЧИВОСТЬЮ РАЗНОСТНОЙ СХЕМЫ называется непрерывная зависимость решения разностной задачи от правых частей и граничных условий.

Для линейного оператора схема устойчива, если ||и_л|| < С||/_л||, где С — постоянная, не зависящая от шага разностной сетки и входных условий f.

Поясним понятие устойчивости. Ошибки при вычислении начальных и граничных условий и правых частей уравнений из-за ошибок округления и других причин можно рассматривать как возмущения начальных и граничных условий и правых частей уравнений. Очевидно, что разностная краевая задача (или задача с начальными данными) будет корректной и устойчивой, если решение разностной краевой задачи будет незначительно изменяться при малом изменении начальных и граничных условий и правых частей, связанном со случайными ошибками. В противном случае разностная краевая задача является неустойчивой. Важно отметить, что для неустойчивых разностных схем уменьшение шага сетки не приводит к устойчивости, поскольку любые малые возмущения решения со временем неограниченно возрастают.

ТЕОРЕМА. Пусть разностная задача L_hu_h = f_h аппроксимирует оператор Lu = / на решении с порядком р и устойчива. Тогда решение u_h сходится к точному решению и имеет место оценка ||u — uj < C_ph^p, где С_р — постоянная, не зависящая от шага Л и входных данных f.