Модель неопределенности выбора весовых коэффициентов на основе метода рандомизации

Для преодоления указанных недостатков классического метода рыночных мультипликаторов можно предложить в качестве модели неопределенности выбора весовых коэффициентов на каждом из этапов метода рыночных мультипликаторов принцип рандомизации, который заключается в том, что вместо детерминированных равных значений весовых коэффициентов используются случайные величины, имеющие известное совместное распределение вероятностей на соответствующем множестве. Рассмотрим математическую постановку указанной задачи.

Введем следующие обозначения:

К — количество эталонных компаний;

L — количество производственно-финансовых показателей, используемых при расчете рыночных мультипликаторов;

q_kl — значение /-го показателя для k-и эталонной компании, k = 1,…, К, L;

C_k — текущая рыночная капитализация k-и эталонной компании, k=l,…, К:

Q

I_к1 = —— частный рыночный мультипликатор k-й эталонной компа- Як!

нии, соответствующий /-му показателю, k = 1,…, К, I = 1,…, L;

w_k — весовой коэффициент (относительная значимость) k-и эталонной компании при расчете рыночных мультипликаторов, w_k >0, k = 1, К,.

щ +w₂ +…+w_K = 1.

В предлагаемой модели переменные w_k являются случайными величинами, моделирующими неопределенность выбора весовых коэффициентов, которые отражают относительную значимость для анализа каждой из эталонных компаний. Тогда значения рыночных мультипликаторов, соответствующих различным показателям, также являются случайными величинами и рассчитываются по формуле.

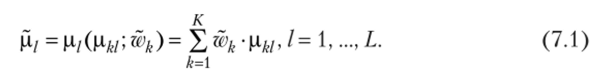
Отметим, что рыночные мультипликаторы Д_kI являются случайными величинами, так как случайными величинами являются весовые коэффициенты w = (w_{f…, w_K), что отражает неопределенный характер их выбора. В качестве оценки отдельного рыночного мультипликатора целесообразно взять математическое ожидание соответствующей ему случайной величины:

а в качестве точности оценки — стандартное отклонение.

где дисперсия случайной величины Д/ определяется по формуле.

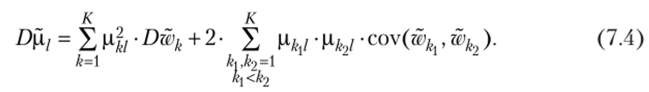
Тогда интервал Д/ ± 5) можно считать интервальной оценкой рыночного мультипликатора, соответствующего /-му производственно-финансовому показателю.

Обратимся теперь к вопросу вычисления математических ожиданий, дисперсий и ковариаций весовых коэффициентов w = (w_v…, w_K). Как упоминалось выше, для моделирования неопределенности выбора весов используется метод рандомизации. В данном конкретном случае будем.

считать, что веса отсчитываются с заданным дискретным шагом —, где.

п

п > 0. Таким образом, w_k е 10, —, —,——, 11, а все вместе весовые коэффи;

[ п п п J.

циенты принадлежат дискретному (К — 1)-мерному симплексу, определяемому следующим образом:

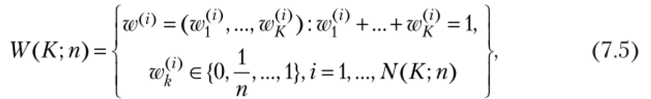
где количество элементов N (K; п) множества W (K; п) определяется, но формуле^[1]

В том случае, когда лицо, принимающее инвестиционные решения, не имеет дополнительной информации относительно значимости весовых коэффициентов w_k, выбор весов осуществляется равновероятно (равномерно) из всего множества W (K; п). В данной ситуации значения для математического ожидания, дисперсии и ковариаций весовых коэффициентов можно получить в явном виде:

где k, k_]y k₂ = 1,К.

На основе формул (7.2)—(7.4) и (7.6)—(7.8) можно построить оценки математического ожидания и дисперсии рыночных мультипликаторов для рассматриваемых производственно-финансовых показателей:

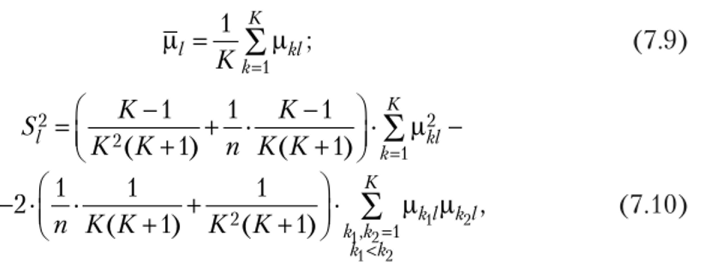
где /= 1,L.

В случае отсутствия дополнительной информации оценка рыночных мультипликаторов (7.9) полностью соответствует классическому методу рыночных мультипликаторов. Однако полученная при этом оценка точности расчета (7.10) позволяет строить интервальные оценки указанных показателей.

В большинстве случаев при оценке реальных предприятий инвестор может располагать дополнительной информацией об относительной значимости отдельных весовых коэффициентов, соответствующих эталонным компаниям. Как правило, подобная информация, задаваемая в виде отношений «акции одной компании по своим фундаментальным показателям оценены рынком лучше, чем другой», носит нечисловой характер. Подобную информацию формально можно представить в виде системы неравенств относительно элементов набора весовых коэффициентов w = (w_it…, w_K):

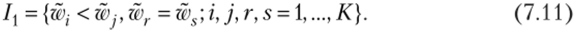
Учет дополнительной информации, описываемой множеством 1_Х и налагающей определенные ограничения на весовые коэффициенты, позволяет сформировать более узкое множество допустимых весовых коэффициентов W (K; п 1_{) с W (K; п), содержащее меньшее число элементов N (K; п 1_{) < < N (K; п). Для получения вероятностных характеристик весовых коэффициентов с учетом указанной информации необходимо отобрать из множества W (K; п) элементы, которые удовлетворяют условиям из множества 1_{. Поставленную задачу можно решить путем генерации на ЭВМ всех векторов из множества W (K; п), упорядоченных в лексикографическом порядке¹, с последующим отбором только тех из них, которые удовлетворяют заданным условиям.

Следует заметить, что данный подход к генерированию весовых коэффициентов позволяет получить дополнительные преимущества по времени выполнения в многопоточных приложениях и многопроцессорных системах^[2][3]. Используя полученную выборку, можно вычислить математические ожидания, дисперсии и ковариации весовых коэффициентов, определяющих относительную значимость каждой эталонной компании:

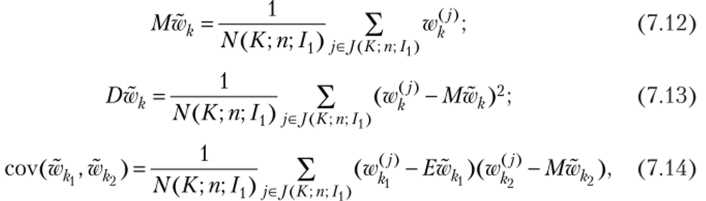
гдеJ (K; п; 1_Х) — множество номеров весов из множества W (K; п), которые удовлетворяют условиям из множества 1_{. Средние значения и дисперсии рыночных мультипликаторов получим, используя формулы (7.2), (7.4) с учетом соотношений (7.12)—(7.14). Таким образом, указанная последовательность действий позволяет построить интервальные оценки рыночных мультипликаторов, учитывающих дополнительную нечисловую информацию о степени недооцененности или переоцененное™ акций эталонных компаний, которая имеется у аналитика.

Перейдем к процедуре построения оценок справедливой стоимости акций анализируемых компаний, которые не входят в эталонную выборку.

Будем в дальнейшем считать, что производится оценка справедливой стоимости акций одной компании. Для данной компании известны значения всех производственно-финансовых показателей, рыночные мультипликаторы которых построены на предыдущем этапе. Напомним, что в рамках метода рыночных мультипликаторов утверждается, что справедливая стоимость акционерного капитала анализируемой компании, но каждому показателю является произведением значения показателя на соответствующее среднерыночное значение мультипликатора:

где g/ — значение /-го производственно-финансового показателя анализируемой компании; Q — справедливая стоимость акционерного капитала анализируемой компании по /-му показателю. Отметим, что в рамках описываемого подхода стоимость акционерного капитала С/ является случайной величиной в силу случайности рыночных мультипликаторов. В качестве оценки стоимости акционерного капитала по отдельному показателю естественно взять математическое ожидание случайной величины Q, а в качестве характеристики точности такой оценки — ее стандартное отклонение:

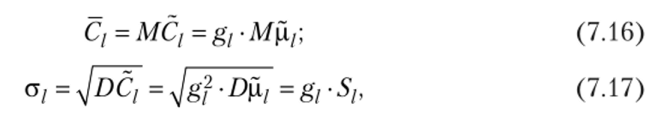
где / = 1,…, L

Справедливая стоимость акционерного капитала оцениваемой компании С представляет собой взвешенную сумму соответствующих стоимостей по каждому из рассматриваемых показателей:

где V/ — весовые коэффициенты, отражающие значимость соответствующих производственно-финансовых показателей в совокупной оценке капитала. Для моделирования неопределенности выбора весовых коэффициентов V/ можно применить подход, аналогичный представленному выше при определении весов эталонных компаний, а именно, будем использовать случайный вектор v = (v₁,…, v_?), равномерно распределенный на дискретном симплексе.

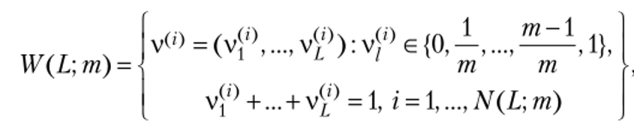
где—шаг отсчета весовых коэффициентов; N (L; т) = С[~^х_т__{ — число элементов множества W (L; т). Таким образом, справедливая стоимость акционерного капитала оцениваемой компании становится дважды рандомизированной:

Для построения оценки справедливой стоимости акционерного капитала компании рассчитаем математическое ожидание случайной величины С.

Точность такой оценки отражает дисперсия (стандартное отклонение) указанной случайной величины. В предположении о независимости V/ и Cj получим следующие соотношения:

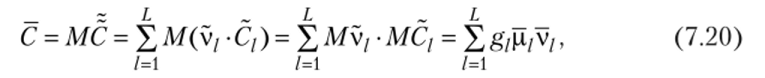
где V/ — математическое ожидание весового коэффициента V/,.

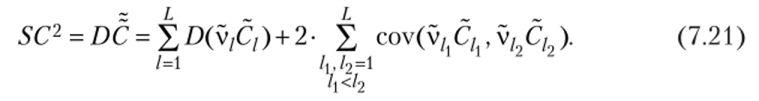
Проведя ряд преобразований и учитывая независимость v, и С/, можно убедиться, что Z)(v_/C_/) = (Dv_/ + vf)Gf + DvjCf_y a cov (v_/jC_/i, v^C_/v) = = Cj_i • Q₂ • cov (v_/j, V/₂). С учетом приведенных соотношений и формулы.

(7.21) получим.

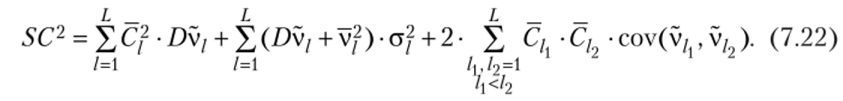
Из формулы (7.22) следует, что на точность оценки справедливой стоимости акционерного капитала компании оказывают совместное влияние как абсолютные значения оценок данного капитала по различным показателям, так и погрешности вычисления этих оценок, связанные в том числе с неопределенностью в справедливой оценке рынком эталонных компаний. Интервал C±SC является тем самым интервальной оценкой фундаментальной стоимости акционерного капитала компании.

В том случае, когда инвестор не располагает дополнительной информацией относительно значимости различных производственно-финансовых показателей в совокупной оценке справедливой стоимости акционерного капитала, т. е. информацией о значениях весовых коэффициентов в соотношении (7.18), можно указать формулы для вычисления числовых характеристик данных весов:

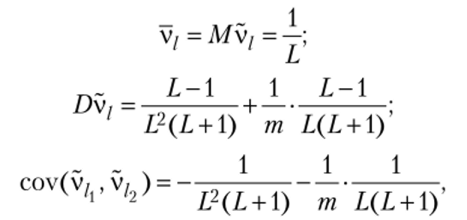
где /, /₂= 1,L.

Однако при оценке стоимости компаний инвестор, как правило, может выделить показатели, которые в большей степени влияют на динамику курсовой стоимости акций. Такую информацию, отражающую указанные предпочтения, можно представить в виде множества /₂ ⁼ (v, < V.-, v, = г, j, r, s = 1,…, I}. Осуществляя генерацию весовых коэффициентов из множества W (JL т /₂) с W (L; т), состоящего только из тех элементов множества W (L; т), которые удовлетворяют ограничениям из /₂, можно получить необходимые характеристики весов (математические ожидания, дисперсии и ковариации), основываясь на формулах, аналогичных формулам (7.12)—(7.14).

Таким образом, приведенная двухшаговая процедура позволяет получить оценку справедливой стоимости акционерного капитала анализируемых компаний с учетом нечисловой информации об относительной значимости различного рода показателей, характеризующих деятельность данных компаний.

• [1] Хованов II. В. Анализ и синтез показателей при информационном дефиците. СПб.: Изд-во Санкт-Петербургского университета, 1996.
• [2] Кнут Д. Э. Искусство программирования. Т. 3. Сортировка и поиск. М.: Вильямс, 2001.
• [3] Хованов II. В. Указ. соч.