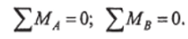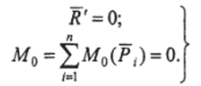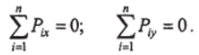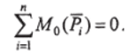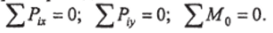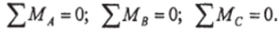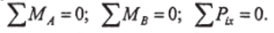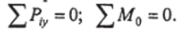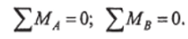Уравнения равновесия плоской системы сил

Плоская система сил может быть приведена к главному вектору R' и главному моменту' Мо, поэтому условия равновесия сил на плоскости имеют вид.

Итак, для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат равнялись нулю и чтобы алгебраическая сумма моментов этих сил относительно любой точки плоскости также равнялась нулю.

Величину главного вектора можно определить через проекции всех сил системы на координатные оси х и у. Для равновесия необходимо, чтобы главный вектор был равен нулю. При соблюдении этого условия получим.

Кроме того, для равновесия необходимо, чтобы главный момент также был равен нулю, то есть.

В дальнейшем для уравнения равновесия при решении задач будем применять более компактную схему записи, не применяя при букве Е обозначения /=1 и п.

Уравнения равновесия произвольной плоской системы сил могут быть представлены в трёх формах.

1. Основная форма приведена выше и записывается в виде:

2. Выбрав три произвольные точки Л, В, Си приравняв нулю сумму моментов относительно каждой из них, можно получить следующие три уравнения равновесия: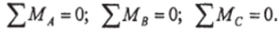

3. Эта форма представляет собой равенство нулю сумм моментов относительно двух произвольных точек, А и В и равенство нулю суммы проекций на некоторую ось х, то есть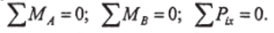

При пользовании этой формулой необходимо, чтобы ось х не была перпендикулярна линии, соединяющей точки А и В.

Для системы параллельных сил, выбрав одну из осей проекций параллельной этим силам, а другую — перпендикулярной к ним, получим существенные упрощения.

Первая форма уравнений равновесия в этом случае примет вид.

Вторая и третья формы уравнений равновесия примут одинаковый вид